运用ARCS教育理论改进高中算法与程序设计教学

☆杨晓峰

（上海松江二中现代教育技术组，上海 201600）

算法与程序设计是上海市高中信息科技教学的三个选修模块之一。笔者在多年的高中算法与程序设计教学中发现，学生学习的主动性不足，部分学生反映“算法与程序设计的学习枯燥乏味”。

笔者以为产生这种情况的根本原因是学生的学习动机不足。很多教师专注于教学方法的优化和教学设计的推陈出新，却忽略了对学生学习动机的研究。高中的算法与程序设计教学需要学生积极主动的思考，培养学生的抽象思维，进行知识的建构。学生在没有明确为什么学习算法与程序设计，没有切身体验到学习内容对自己的学习和生活有什么帮助的情况下，他们的学习只能是被动地学习。而缺乏了学生积极主动的参与，无论教师如何改进教学方法，教学的效果必然大打折扣。

ARCS动机设计模式是由美国南佛罗里达大学的心理学教授J.M.Keller提出的。这一模式认为，影响学生学习动机的因素有四类：注意（attention）、切身性（relevance）、自信心（confidence）、满足感（satisfaction）。因此，教师在进行教学设计的同时，还应该进行适当的动机设计，即针对学生群体的动机状况和教学内容的特点设计相应的动机策略，设法使教学过程能够引起并维持学生的注意、建立起教学与学生之间的切身性、使学生产生并维持对学习的自信心、并提供一种满意感，那么教学就能激发学生的学习动机。

笔者运用ARCS教育理论，在高中算法与程序设计教学中进行了实践研究。以激发学生的学习动机，促进学生主动学习为目标，在研究过程中不断改进和优化我校的算法与程序设计课程。

一、注意策略

注意是学习者进行学习活动的前提条件。教学应该有效地激发学生对教学内容的好奇心。在学生产生学习兴趣的前提下有效维持学生的注意力，才能使学生主动地投入到高效率的学习中。

1.唤起感知，使学生产生学习兴趣

对于高中学生而言，算法和程序设计不仅是一门全新的课程，更是一个全新的学习领域。学生必然会产生“我为什么要学，学了有什么用”之类的疑问。这样的疑问，并非开展教学活动的绊脚石。相反，如果很好解决这样的疑问，帮助学生看到学习算法和程序设计的美好前景，反而会有效地激发学生的学习兴趣，成为学生主动学习的助推器。

以“验证歌德巴赫猜想”作为课题引入，开始算法和程序设计课程第一节课的教学。方案如下：

（1）连续设问：“大家了解数学皇冠上璀璨的明珠——歌德巴赫猜想吗？”、“根据歌德巴赫猜想，偶数8可以是哪两个质数的和呢？”。大多数学生对于歌德巴赫猜想是耳熟能详的，所以，很容易就回答了以上两个问题。

（2）继续提问：“大家有没有办法算出2388是哪两个质数的和呢？”学生开始拿出草稿纸进行计算。由于缺少正确的算法，他们的计算更多的是在碰运气地凑两个质数。题目的复杂让大多数学生在一段徒劳无功地尝试后选择了放弃。

（3）程序演示：教师运行设计好的程序，在瞬间算出了正确的解答：1187＋1201＝2388。学生中一下子炸开了锅。有的学生在赞叹：“太给力了！”有的学生迫不及待地问：“老师，快告诉我们怎么编这个程序吧！”。

（4）教师引导：现在讲解这个程序，大家理解上会有一些难度。但是，在大家学习了程序设计的知识和算法的思想后，我确信每个同学都能编写这样的程序。

2.唤起探究，启发积极的思考

教学中提出一些在学生认知最近发展区内的难题，虽然学生现阶段无法独立解决，却能够有效唤起学生的探究活动，启发积极的思考。而对这些问题的求解，可以是我们进行下一阶段教学的“润滑剂”。

在学生掌握分支结构的基础上，提出分支结构无法解决的难题，然后提出循环结构并有效解决难题。这不仅使新教学内容的引入自然顺畅，也让学生充分了解了循环结构的用途和适用范围。

3.多变的教学，维持学生的注意力

随着教学过程的开展，学生的学习兴趣和热情会逐渐地消退，注意力也会开始分散。教师可以通过教育形式和教学媒体的改变，或是教师本人的肢体语言，或是表达风格的切换（幽默－严肃、大声－轻声等）以保持学生的注意力。

从教育心理学的角度看，有意义、有变化的教学内容更容易保持学生的注意力。

在讲解符号“＋”在字符中的连接作用时，笔者按照常规举了个例子。A＝“a”；B＝“b”；C＝A＋B，所以，C的值是“ab”；D＝B＋A，所以，D的值是“ba”。学生的反应冷淡，自己也觉得索然无味。

于是在下一节课的教学中，笔者更换了举例的内容。A＝“开”；B＝“放”；C＝A＋B，所以，C 的值是“开放”；D＝B＋A，所以，D的值是什么呢？教学到这步，学生已经抢着回答了“放开”。很多学生在这个时刻发出了会心的笑声。

二、切身性策略

通过解决与学生切身相关的问题，使学生认识到算法与程序设计的学习与自己的学习和生活密切相关，与过去的经验和以前学习的知识相互关联。

1.明确学习目的

明确学习的目的并取得学生的认同，对提高学习的主动性和保持学生的注意力至关重要。通过设计评委打分程序，并实际应用于社团评比活动中，使学生明确学习算法与程序设计有助于解决生活中的实际问题。通过一题多解，使学生感受到学习促进了自己创新思维的培养，思维的广度和深度获得了提升。类似的教学既突显了算法与程序设计教学的特点，也让学生切身感受到自身能力的提升。

2.“熟悉性”的利用

利用学生经验中熟悉的东西进行教学，从学生已有的生活经验和知识体系出发开展教学，能有效降低学生参与新的教学活动的陌生感，提升学习的热情。

在讲解逻辑表达式的运算规则中，采用学生比较熟悉的单科奖学金和综合奖学金进行举例。

条件1：语文成绩超过90分。条件2：数学成绩超过90分。

P1（单科奖学金）的规则：只要有一门课超过90分。

P2（综合奖学金）的规则：必须两门课都超过90分。

由于以上规则是建立在学生熟知的基础上，在下面学习逻辑运算符“AND”和“OR”的运算规则时，学生的学习显得非常的顺利。

条件1 条件2 P1（条件1 AND条件2） P2（条件1或 条件2）否否 否 否否是 否 是是否 否 是是是 是 是

在教师进行了必要的引导后，大部分的答案学生都可以自己推导出来了。

3.构建学习共同体，丰富学习体验

算法与程序设计要消除学生个人封闭学习的“偏见”，要挖掘共同学习的学习内容，形成浓烈的学习氛围。

在模块化程序设计教学中，笔者引导学生将设计评委打分程序的问题分解成四个模块，并由四个小组各自完成一个模块的求解。

第1小组：输入8个评委的分数，并保存在数组a。

第2小组：根据数组中的分数，计算最高分，保存在max变量中。

第3小组：根据数组中的分数，计算最低分，保存在min变量中。

第4小组：根据数组中的分数，计算总分，保存在sum变量中。

当四个小组分别完成各自的任务后，计算平均分的工作就显而易见了。学生利用(sum－max－min)/6就求出了平均分。

以上教学让学生依靠集体的力量完成了工作量相对较大的任务，体验了分工与合作的过程，也加深了对模块化程序设计思想的认识。

4.符合思维习惯，帮助学生进行知识建构

算法与程序设计的很多思想对学生而言是全新的，是对常规的顺序式的思维方式的突破。在教学中需要从学生已有的思维习惯入手，强调教学过程的循序渐进，帮助学生进行知识的建构。

在引入循环结构教学时，笔者采用了计算6个班级的捐款总额的例子。

学生固有的思维方式是顺序式的依次累加。特别是学生习惯于将6个数字在草稿纸上全部记下来以后，然后计算总额。为此，笔者故意设置障碍，要求不得使用草稿纸。这样学生不得不采用记住一个数值，和已有的总额累加，再获取一个数值，再和已有的总额累加的方法。这样，学生的计算方法就符合了计算机利用循环结构进行累加求和的方法，体验到了循环体“输入一个值，累加求和”反复执行的过程。

在此基础上，笔者引导学生总结循环体“输入一个值，累加求和”，分析循环次数，得出循环的结束条件，并确定循环变量的初值。与此同步，笔者在黑板上将上述的引导过程通过流程图逐步勾勒出循环结构解决上述问题的过程，实现对知识的逐步建构。

步骤1：总结循环体 步骤2：分析循环次数，得出循环的结束条件步骤 3：并确定循环变量的初值

三、自信策略

通过学习算法与程序设计，逐步解决从前无法解决的问题，掌握解决问题的方法，体验到自身能力的提高，帮助学生在学习中树立自信。提升学生的自信，是教学活动的目标。在教学过程中获得的自信，也有助于学生在下一阶段的学习中主动的投入。

1.强化学生成功源于努力的信念

在“验证歌德巴赫猜想”的课题中，可以通过以下问题的设置。“如果n为偶数，a和b为所求的两个质数，在确定a的值以后，b的值如何确定？”、“确定了b＝n－a以后，分析 a的取值范围？”、“当 a从 2到 n/2逐步取值时，b的值在如何变化？”、“如何验证a是否为质数？”、“如何验证a和 b同为质数？”，“当a和 b不同为质数时，a和b如何取值，逐步缩小取值范围？”、“循环的结束条件是什么？”。最终学生得出a从 2到 n/2逐步取值，b始终取值为 n－a，当 a和 b同为质数时就得到了正确的答案。让学生充分发挥学习的主动性，在不断求解新问题的过程中获取知识，在一步步的成功中看到自身能力的提升，从而增强学习的兴趣和信心。教师对学生的每一份努力、每一次进步，应给予及时而适当的表扬，激发学生积极的学习心态。

2.培养创新思维，强化自信

通过一题多解等方式，突破常规思维方式，培养学生的创新意识和创造能力，强化学习的自信心。

在学习交换两个变量的值时，教师先讲解常规的解题方法。然后提出不用中间变量，引导学生思考更高效的解题方法。

常规方法 创新方法一 创新方法二a＝5 b＝3 t＝a a＝b b＝t a＝5 b＝3 a＝a＋b b＝a－b a＝a－b a＝5 b＝3 a＝a觹b b＝a/b a＝a/b

四、满足感策略

在教学中教师应组织强化，帮助学生达到自己的学习期望，使学生从学习中获得满足。而这份从学习中获得的满足感必将转化为进一步主动学习的动力。

1.内部强化

在评委打分程序的教学中，如果只是简单地实现总分除以人数得出平均分是不能真正让学生满意的。经验告诉他们实际比赛中使用的评委打分程序并非如此。这里需要引入最值问题的求解。只有让学生掌握了求解最大值和最小值的方法，并在此基础上实现了“计算总分，去掉一个最高分，去掉一个最低分，最后得出平均分”这一符合实际应用的方法后，他们才会略感满足。

在和实际应用的比较中，学生又会发现程序新的不足。刚才设计的程序只能实现多个评委对一个学生的打分。对该学生的打分完成后，程序就结束了。显然现实中并非如此。这里又需要引入双重循环的概念，使用外部循环处理多个学生，使用内部循环实现多个评委对一个学生的打分。

在与现实应用的不断比较中，学生不断地发现现有程序的不足。通过进一步深入地学习，他们不仅拓宽了自己的知识面，更对自己的程序更具实用价值感到满意。

意识到自己的程序具有使用价值以后，学生总是希望尽可能地在实际生活中使用它。学校的社团评比提供了应用评委打分程序的舞台。教师帮助解决了电脑和投影设备等环境的布置。学生则对程序运行界面作了进一步的美化，在得出一个相对较高的得分时，程序还会发出惊叹的拟人声音。使用电脑程序进行评委打分的过程是令人满意的。这不仅提高了评委打分的效率，也让设计程序的学生获得了成就感。

教学中提供给学生真实的问题解决环境，让他们应用已有知识解决实际问题。在此过程中，让每一位学生充分发表自己的见解，积极鼓励学生大胆尝试并提供必要的引导和帮助。当这些大胆的尝试取得积极的成果，并且符合学生的预期时，学生的学习动机就会被激发，维持在一个较高的水平上。

2.注重方法教学，提升学习效率

帮助学生提炼解题方法，让学生感受到自己学习的不是解决某个问题的步骤，而是解决一类问题的方法。这不仅有助于学生知识迁移能力的培养，更能帮助学生提升学习的效率。

通过例题“求 65＋90＋10＋35＋75的和 s”学习了累加求和的方法后，给出相似的题目“求s＝1＋2＋3＋……＋n的值，其中n由键盘输入”。学生发现这个问题的求解仍然是累加求和的方法，只是循环的次数不是事先确定的，而是在程序执行过程中由键盘输入的。这时给出进一步的题目“求s＝2＋4＋6＋……＋n的值，其中n为偶数，由键盘输入。”学生会发现这个题目的求解也是累加求和的方法，只是在上一题的解题基础上增加了“循环变量的值每次增加2”的变化。通过相似题目的类比和思考的逐步深入，学习累加求和方法的适用范围。

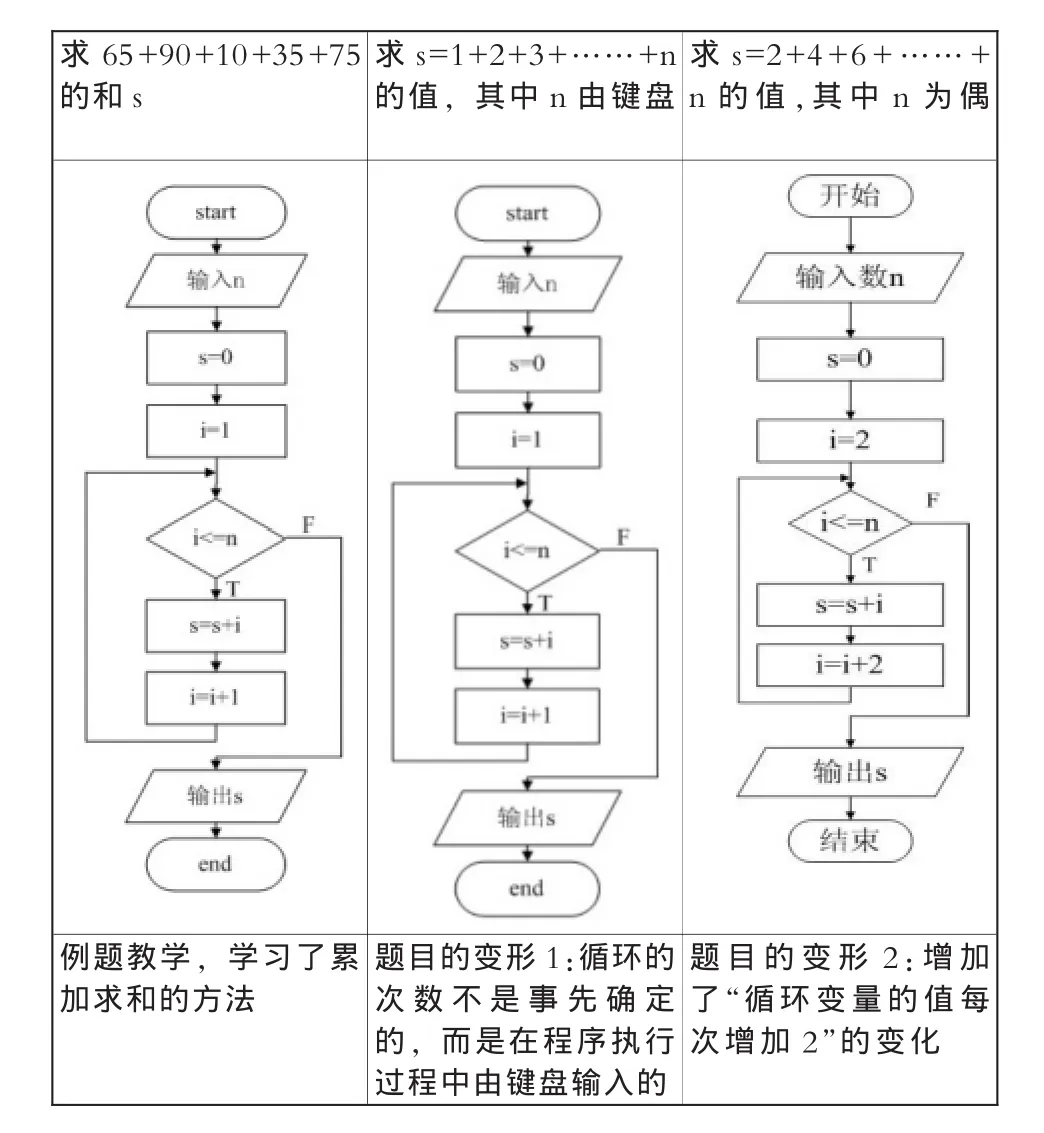
求 65＋90＋10＋35＋75的和s求 s＝1＋2＋3＋……＋n的值，其中n由键盘求 s＝2＋4＋6＋……＋n的值，其中n为偶例题教学，学习了累加求和的方法题目的变形1：循环的次数不是事先确定的，而是在程序执行过程中由键盘输入的题目的变形 2：增加了“循环变量的值每次增加2”的变化

笔者将ARCS动机设计模式运用于高中算法与程序设计教学，在高一年级的算法与程序设计教学中进行了5个月的实践。实施策略前后，在实验班和对照班的学生中分别进行了“高中算法与程序设计学习动机调查问卷”的调查。通过对5个月前后的调查结果和学业绩效的分析、比较，发现学生的学习动机、情感反应和学业绩效均有一定程度的提高。

运用ARCS教育理论，从注意、切身性、自信心、满足感四个维度促进学生的主动学习，使学生成为学习的主人。学生主动地学习，必将推动三维教学目标的有效实现。

[1]郭德俊,汪玲,李玲.ARCS动机设计模式[J].首都师范大学学报（社会科学版）,1999,(5).

[2]党凤良,刘恩山.高中生学习生物学动机的初步研究[J].生物学通报,2003,(7).

[3]张祖忻.如何将动机原理整合于教学设计过程[J].开放教育研究,2003,(2).