测定双轴磁传感器正交度的椭圆拟合法

李 伟，卢俊杰

（中国船舶重工集团公司第七一〇研究所，湖北 宜昌 443003）

0 引言

磁传感器的正交度是双轴或三轴磁传感器的重要指标，在精密磁测量领域［1］和高精度磁罗盘的应用场合［2］，以及高分辨力的磁场探测领域，该指标尤为重要。目前工程上常用的磁传感器正交角度的测试方法是磁场投影法。

磁场投影法对设备的要求较高，需要精密的磁场产生设备——磁场线圈，同时，操作步骤复杂，需要完成磁传感器的轴与磁场线圈的轴对准操作（该操作为精密装配操作，耗时较长）。鉴于磁场投影法的上述缺点，本文提出了一种利用椭圆拟合测定双轴磁传感器正交角度的方法。

1 椭圆拟合及其算法

为了比较椭圆拟合测定双轴磁传感器正交角度的方法和磁场投影法，先简要介绍磁场投影法。

1．1 磁场投影法

磁场投影法的示意图如图1：待测定x轴与y轴的夹角α，则在x轴方向上施加磁场B，测量y轴的输出记为By，则依据矢量的投影定理有：

式（1）中，磁场B、磁传感器的输出By均由标准的磁测量仪器测定。

图1 磁场投影法的示意图Fig．1 Principle schematic of magnetic field projecting algorith m

1．2 椭圆拟合及其算法

椭圆拟合是计算机视觉中的常见问题，在图像处理、机器视觉、模式识别等领域都有广泛的应用［3］。

二次曲线方程的一般形式为［4］：

当式（2）满足约束条件式（3）时，该二次曲线为椭圆。

当二次曲线为椭圆时，对于式（2）的A、B、C、D、E、F这六个参数可以采用最小二乘法来进行求解，即最小二乘法椭圆拟合。设观测点坐标为（xi，yi），其中i＝1～n，则利用式（2）可以构建线性方程组，如下：

式中，i＝1～n且（n≥5）。

上述线性方程组写成矩阵形式如下：

当测点数n＝5时，线性方程组有唯一解。

当测点数n＞5时，方程（6）为矛盾方程，一般用最小二乘法求解。此时方程（6）的最小二乘解为［5］：

将上述最小二乘结果代入式（2）即可求出椭圆曲线的一般方程：

1．3 两个单频正弦信号的合成轨迹

法国科学家Jules Lissajous1875年在法国巴黎科学院发表的论文中用李萨如（Lissajous）图形来表征两个单频正弦信号的合成输出［6］。当两个信号的频率相同时，李萨如图形为椭圆。设有两个正弦信号，其幅度分别为A1、A2，角频率均为ω，初相角分别为ψ1、ψ2，其数学表达式如式（9）所示：

定义相差α＝ψ1－ψ2，以式（9）中的X为横坐标，Y为纵坐标，绘制出不同相差的李萨如图形，如图2所示。

图2 不同相位差的李萨如图形Fig．2 Lissajous figures vs phase－difference

2 测定双轴磁传感器正交度的椭圆拟合法

2．1 相位差—纵向坐标差的转换

将双轴磁传感器置于水平转台上旋转一周，此时磁传感器所测得的磁场是地磁场B。记双轴磁传感器的输出分别为Bx、By，其对应的灵敏度分别为Sx、Sy，磁传感器两轴间的夹角为α，传感器的零点参数分别为X0、Y0，则双轴传感器的输出为：

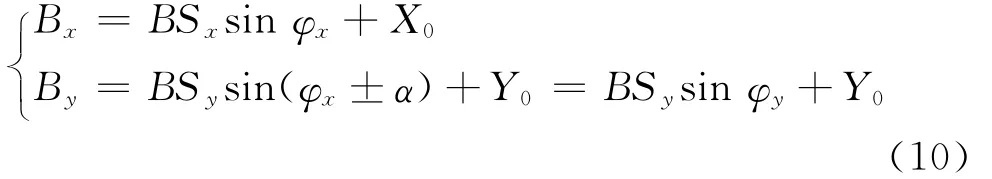
式（10）中，φx、φx±α分别为磁传感器x轴初始相位和y轴初始相位，φx对应于磁传感器的初始方位，该参数由装夹时决定。α为传感器的固有特性，主要取决于磁传感器的机械安装误差。将双轴磁传感器在水平面内转动一圈，记录对应的角度和磁传感器的输出，在同一坐标系中绘制双轴磁传感器的输出曲线，可得到如图3所示的图形。

图3 双轴磁传感器的输出曲线Fig．3 Output of dual－axis magnetic sensor

图3 中，输出曲线的相位差φx－φy即为双轴磁传感器的夹角，曲线的峰峰值对应于磁传感器的灵敏度参数，曲线的直流分量对应于磁传感器的零点参数。通过数学方法求解出曲线的解析表达式，即可求出传感器两轴之间的夹角。

按照李萨如图形的合成轨迹方法，将式（10）中的Bx、By绘制成图形，其中Bx映射到x轴，By映射到y轴，如图4所示。

图4 双轴磁传感器的李萨如图形Fig．4 Lissajous figure of dual－axis magnetic sensor

图4 中，椭圆的中心由磁传感器的零点确定。椭圆上纵坐标的极值点P（xP，yP）、Q（xQ，yQ）由式（10）中By来确定，由式（10）有：

如图4所示，记线段PQ的长度为S，则由式（11）可得：

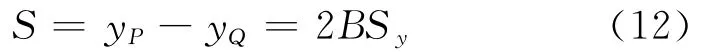
取式（10）中x轴的相位为0值，即φx＝0，则此时有：

式（13）对应于图4中横坐标x＝X0的点，亦即M（xM，yM）、N（xN，yN）两点，即 M 点坐标为（X0，BSysinα＋Y0），N点坐标为（X0，－BSysinα＋Y0）。记图4中线段MN 的长度为T，由式（13）可得：

联立式（12）、式（14）两式，可得到：

由式（15）可知，只需要求得图4中的线段长度T、S值，亦即只要能求得拟合椭圆上P、Q、M、N四点的坐标，则磁传感器的夹角可以由式（15）求得。

2．2 线段长度S、T的求解

由图4知欲求线段长度S、T，只需求得拟合椭圆上P、Q、M、N四点的纵坐标即可，即：

图4中P、Q分别为由拟合椭圆方程（8）所确定的隐函数y（x）的极大值点和极小值点，则根据高等数学中求解极值点的一般方法，令H（x，y）＝ax2＋bxy＋cy2＋dx＋ey＋f，则结合式（16）～式（21）可以解得S、T 的关于a、b、c、d、e、f的表达式如下：

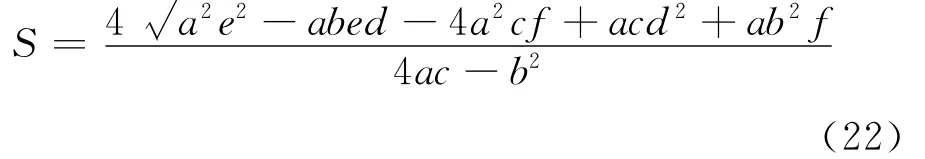
2．3 双轴磁传感器正交角度测定步骤

根据上述分析，椭圆拟合法测定双轴磁传感器正交度的方法的测定步骤如下：

1）将待测双轴磁传感器放置在水平转台上，旋转水平转台，测定至少5个不同测试点的双轴磁场数据。

2）根据1．2节所述的椭圆拟合及其算法，利用步骤1）所测得的试验数据进行椭圆拟合，得出该传感器的椭圆方程。

3）将步骤2）中椭圆方程的参数代入式（22）、式（23）求出S、T。

4）将步骤3）所求的S、T值代入式（15）即可求出双轴磁传感器的正交角度。

3 磁传感器的实际测定

为验证本文提出算法的正确性，特随机挑选了1台磁传感器按照上述2．3节的测定步骤进行测试。所用磁传感器为国防弱磁一级计量站的Mcc201型数字磁传感器，如图5所示。

图5 磁传感器测试图Fig．5 Ort hogonality measurement of dual－axis magnetic sensor

Mcc201型数字磁传感器有内置的ADC芯片，直接输出数字量，故无需电压表来测量电压。调整转台使磁传感器水平放置，转动转台，记录磁传感器两个通道的输出电压数据，无需记录转台的刻度，得到表1的记录数据。

依据式（6）、式（7）、式（8）对表1的磁传感器实测数据进行最小二乘椭圆拟合，得到椭圆参数如表2所示。同时可得到如图6所示的李萨如图形。

表1 磁传感器实测数据表格Tab．1 Output data of dual－axis magnetic seneor

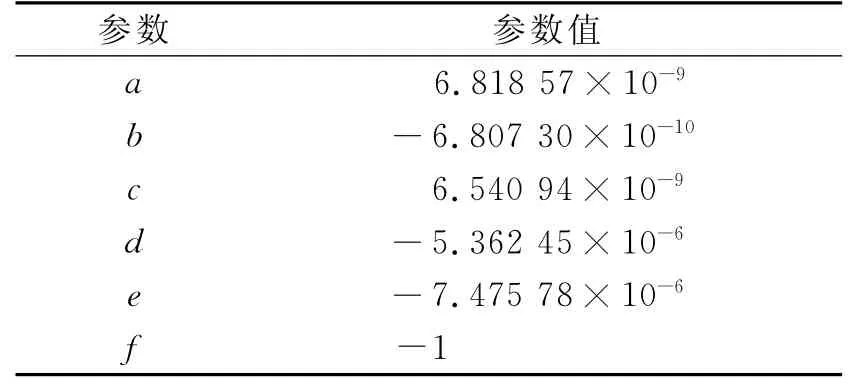
表2 拟合椭圆参数表Tab．2 Fitted ellipse parameters

图6 磁传感器对应的李萨如图形Fig．6 Lissajous figure of the sample dual－axis magnetic sensor

根据式（15）、式（22）、式（23）可以求出，所测得的磁传感器两个轴的正交度，即磁传感器两轴之间的夹角为：

为验证本文提出的方法的正确性，可用磁场投影法进行比对。将磁传感器放置在均匀磁场线圈中，按照1．1节中所述的方法，将测量值代入式（1）、式（2）进行计算得出磁场投影法测得的双轴磁传感器的正交角度为87．10°，与椭圆拟合法测的结果大约只相差0．02°——该差别主要是由磁场投影法的安装和读数误差所致。两种方法比对的结果表明椭圆拟合法的测量结果是正确的。

由于磁矢量投影法对磁传感器的安装有精密的位置对准要求，因此磁传感器的安装误差将直接影响到测量结果的精度。另外磁场线圈的均匀度和稳定度也直接影响磁矢量投影法的测量精度。椭圆拟合测定双轴磁传感器正交度的方法完全消除了安装位置偏差带来的误差和磁场线圈带来磁场误差，因而可达到较高的测量精度。

4 结论

文中所提出的利用椭圆拟合测定双轴磁传感器正交度的方法，首次将磁传感器的双轴输出和李萨如图形结合起来，利用磁传感器输出构成的椭圆参数来解算双轴磁传感器的正交角度。实测实验表明，利用椭圆拟合测定双轴磁传感器正交度的方法可获得比磁矢量投影法更高的测量精度。

同时，从上述试验过程可以看出，文中提出的测量方法主要是基于算法层面的数据处理，将椭圆拟合法测定双轴磁传感器正交度的方法编制成相应的测试软件后，可以进行双轴磁传感器的批量化测试。最后，这种测定正交度的算法也可以为实时修正磁场矢量探测的正交误差提供参考。

［1］朱兆才．三分量磁通门磁变仪探头正交误差对定向的影响［J］．东北地震研究，2004，20（2）：70－75．

［2］李珊，范大鹏，张志勇，等．三轴磁罗盘的高精度误差补偿算法研究［J］．传感器世界，2005（9）：19－22．LI Shan，FAN Dapeng，ZHANG Zhiyong，et al．A highaccuracy algorith m of err or co mpensation for three－axis magnetic compasses［J］．Sensor World，2005（9）：19－22．

［3］史连艳，宋文渊，王红云．基于旋转因子的磁传感器误差补偿改进椭圆法［J］．探测与控制学报，2010，32（2）：5－8．SHI Lianyan，SONG Wenyuan，WANG Hongyun．Improved ellipse met hod f or error co mpensation of magnetoresistive sensors based on rotation factors［J］．Journal of Detection ＆ Contr ol，2010，32（2）：5－8．

［4］刘科利，姚吉利．点位分布与椭圆拟合精度关系研究［J］．山东理工大学学报（自然科学版），2010，24（4）：61－64．LIU Keli，YAO Jili．The relationship bet ween distribution of measuring point and ellipse fitting accuracy［J］．Jour nal of Shandong Unirersity of Technology（Science and Technology），2010，24（4）：61－64．

［5］陈凯，刘青．一种随机化的椭圆拟合方法［J］．计算机工程与科学，2005，27（6）：48－50．CHEN Kai，LIU Qing．A new rando mized method of ellipse fitting［J］．Computer Engineering and Science，2005，27（6）：48－50．

［6］李德堡．工程振动试验分析［M］．北京：清华大学出版社，2004．