基于频谱细化的窗谱拟合算法

顿丛丛，李跃华，王剑桥

（南京理工大学电子工程与光电技术学院，江苏 南京 210094）

0 引言

基于毫米波调频雷达的探测技术结合了毫米波雷达和调频雷达大时宽积、高分辨率、无距离盲区及结构简单等优点已广泛应用于多种武器系统中。毫米波调频探测系统主要是通过对差频信号的谱分析来确定目标距离［1］，但在其实际的调试与应用中发现其测距精度并不甚高。理论上调频探测系统的分辨力受扫频带宽的影响，但增大调制频偏会给系统的实现带来困难，同时，工程中VCO的线性度也不能做到理想，也会影响距离分辨力。故在应用中考虑从测频方法的角度来提高测距精度。现有的提高调频系统测距精度的方法（如文献［2—3］提出的ZFFT和Chir p＿z算法）都是在传统“差频－FFT”测距结构基础上对目标距离谱细化，其提高的分辨率取决于细化倍数的大小。实际中，采样数据一定，细化倍数不能无限增大，细化后的频谱依然为离散谱，频谱估计依然存在着与细化倍数相关的估计误差，提高的分辨率并不能达到理想。针对这些问题，本文提出了ZFFT窗谱拟合算法。

1 调频系统的差频处理方法

1．1 差频－FFT处理

毫米波调频探测系统的原理框图如图1所示。

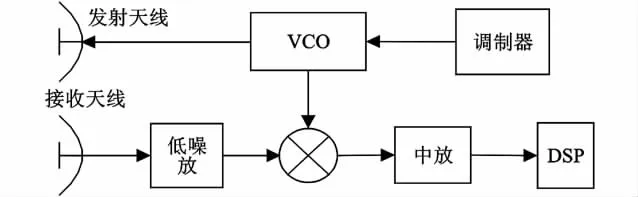
图1 毫米波调频测距系统原理框图Fig．1 Milli meter F M ranging system block

调制的毫米波发射信号与经目标延迟后的回波信号混频后并滤波高频成分得到差频信号，其归一化连续距离谱（只取其正频部分）为式（1）：

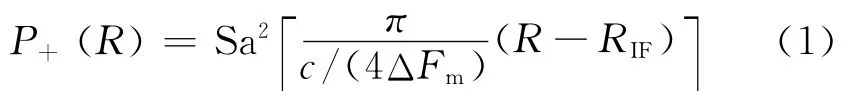
其零点为R＝RIF＋mΔR（m为正整数），其中c／（4ΔFm）为距离分辨力，RIF为回波距离。

调频系统实际的距离谱估计常采用“差频－FFT”处理，时域为A／D以采样率fs采样得到的Ns点数字信号，频域为经N点FFT运算得到的离散距离谱。其频域采样间隔为Δw＝2πfs／N，相应的 距 离 间 隔 为 ΔR ＝ （c／4ΔFm）（fsT／N） ＝（c／4ΔFm）（Ns／N）。

由式（1），当Ns＝N且R＝RIF＋mΔR时，距离谱上只有一根谱线，其对应值为目标真实距离，测距误差为0；当R≠RIF＋mΔR，最大采样点的值偏离距离谱的最大值点，最大误差为c／（8ΔFm），测距精度与分辨力处于同一数量级，没有体现调频系统高精度测距的优势。

从以上分析过程可以看出，造成调频系统测距误差的原因在于距离谱的间隔采样，实质是FFT在单位圆上的N点采样造成，增加FFT点数可减少误差，但运算量大幅度的增加，影响了系统的实时性。

1．2 ZFFT频谱细化处理

ZFFT主要是结合目标频谱一般位于距离谱的局部区域的特性，通过对局部信号进行复调制移频、滤波、降采样后作点数较少的FFT实现对信号频谱的局部细化从而提高分辨率。相对与同样点数的FFT，ZFFT减少了运算量［4］，更适合实时性要求高的系统。

为说明ZFFT的作用，图2给出了该调频系统目标距离3．3 m（对应频率0．456 MHz）时，差频信号128点的FFT和细化8倍后的频谱图，采样率fs＝10 MHz。

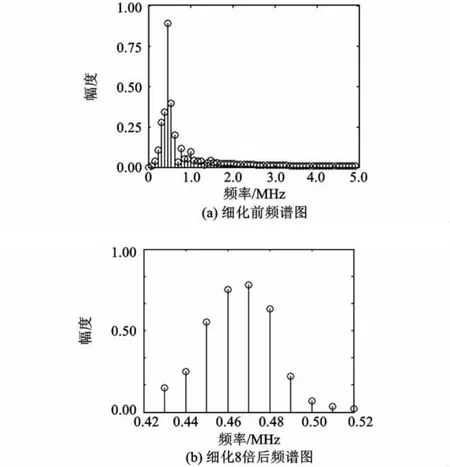
图2 差频信号细化前后频谱Fig．2 The spectr u m bef ore and after refinement

图2 （a）中差频信号128点FFT的频谱分辨率0．08 MHz，估计频率为0．56 MHz；图2（b）中经ZFFT细化8倍后，信号频谱局部得到展宽和细化，分辨率提高为0．01 MHz，估计频率为0．47 MHz。此过程中ZFFT的复乘次数为896，复加次数1 792。做128×8点的FFT可达到同样的分辨率，但其复乘次数为5 120，复加次数为10 240。相对于FFT，ZFFT运算量减少了82%。

由上，ZFFT提高的分辨率是对同样点数的FFT而言的，其细化的倍数与样本点数相关，样本点数有限，最大细化倍数一定。同时由图2（b）可看出，细化后的频谱依然为离散谱，其频谱估计受栅栏效应的影响依然存在着误差，细化倍数越大，误差越少，但对于实际的调频探测系统，采样数据一定，细化倍数受限，提高的测距精度并不理想。

2 ZFFT窗谱拟合算法

ZFFT窗谱拟合的基本思想是在对信号加窗后将目标所在的局部频谱局限在窗函数的主瓣内，并结合ZFFT算法局部频谱细化的优点，将离散的窗谱数据拟合为局部连续的抛物线，在采样数据有限，细化倍数一定的情况下，可克服离散谱的栅栏效应减少频谱估计误差，从而更好地找到目标对应的频率，提高测距精度，其基本原理如图3所示。

图3 ZFFT窗谱拟合原理框图Fig．3 ZFFT window spectrum fitting block

图3 中，若目标为单一静止目标，其理想差频回波信号为中心频率为f0的谐波信号，其傅里叶变换为式（2）：

加窗后的谐波信号为差频信号与窗函数的乘积，频谱为两个信号频谱的卷积，表示如下：

式（3）中，wT0（t）＝w（t－T0／2）为长度为T0的对称窗谱函数。W（f）为频率连续的特殊傅里叶变换［4］，表示为：

取式（3）的正频率部分为信号的单边连续窗谱，如式（5）所示：

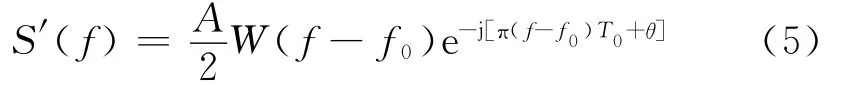
经频移和D倍抽取后的频谱表示为：

fd为频移频率，一般选择为信号的最大谱值和次大谱值对应频率之差与抽取因子即细化倍数D的比值，也可选择为细化频谱范围的1／2，频移后频谱移到了零频附近。

在数字处理中，窗函数的单边连续谱（式（5））为间隔采样的离散窗谱，如图4所示，其对应抽取D倍后的频谱 （式（6））亦为间隔采样的离散谱，如图5所示。

图4 信号连续窗谱的离散谱Fig．4 Discrete spectr u m of continuous window spectr u m

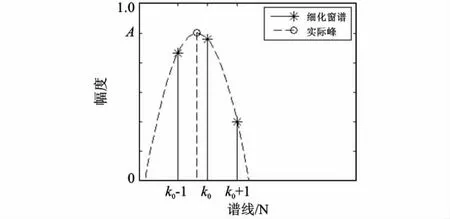
图5 信号连续窗谱细化后的离散谱Fig．5 Discrete spectrum of continuous window spectr u m after refinement

由图4、图5可以看出，信号加窗ZFFT细化后，局部频谱展宽，能更多地看到局部频谱细节，可栅栏效应的存在使细化后的离散谱依然会出现没有找到实际峰值的可能。注意到加窗细化后信号窗谱的主瓣变宽，使得信号的最大采样点及其周围的采样点落于窗谱的近似抛物线上，从而可以利用一个二阶多项式来拟合最大采样点和它相邻的采样点的幅度，更准确地找出实际幅度的峰值位置。

由于实际中目标可能位于ZFFT细化后的两个采样位置之间的峰位置，为便于推导，假定ZFFT采样Y［k］是频率序号k的连续函数。在ZFFT峰位置k0附近，假设Y［k］具有下面的形式：

则峰值k0和其附近测量值的幅值Y［k0－1］，Y［k0＋1］，Y［k0］满足方程组：

拟合多项式的系数可以通过矩阵方程式（8）得到，其系数矩阵满足范德蒙矩阵结构，其行列式为：

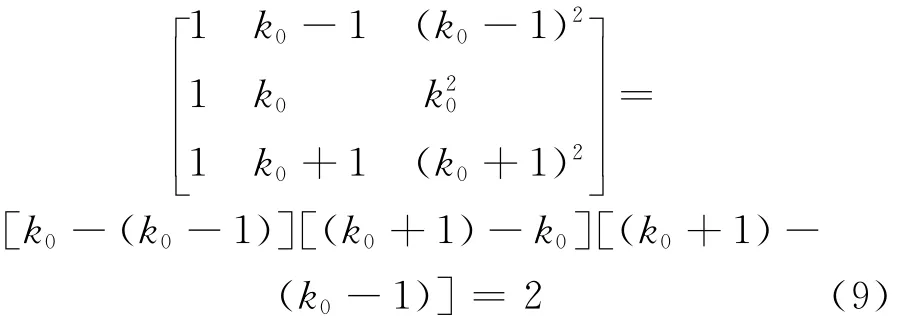
行列式非零，方程组有唯一解，即窗谱的近似抛物线可唯一得到。

假设拟合后的峰值位置为k′＝k0＋Δk，结合式（7）和式（9），Y［k0＋Δk］可表示为：

对Δk求导并令其结果为0，可得Δk从而得出次拟合后的对于k0的相对位置，即：

拟合后的峰值谱线为k0＋Δk。从式（11）可以看出，如果Y［k0－1］和Y［k0＋1］相等，则Δk＝0，中间采样为估计的值，如果Y［k0］与Y［k0＋1］相等，则Δk＝1／2，表示估计的峰值位于两者中间，从直观上看可以得到理想的结果，如图6所示。

图6 窗谱拟合结果Fig．6 Window spectr u m fitting

图6 表明，经拟合后，原本离散的窗谱变为连续窗谱的近似抛物线，可根据式（11）Δk的表达式找到峰值的相对位置，找到拟合后的峰值谱线k0＋Δk，从而克服由于栅栏效应造成的估计误差。

从实现的过程也可以看出，信号的加窗ZFFT细化，只需要少量的FFT计算和低通滤波，低通滤波可以采用比较成熟的FIR滤波器，而拟合的过程仅需要找到局部细化范围的最大值及其周围的几根谱线，就可以方便地计算出拟合后的最大频谱值对应的频率的修正量，其计算量增加很少，符合系统的实时性要求。

3 计算与实验分析

为验证上述方法的有效性，以某项目中研制的毫米波调频探测系统为例进行了实测数据验证分析。该系统采用三角波调制，系统参数为：载频f1＝52 GHz，频偏ΔFm＝320 MHz，调制频率fm＝30 k Hz，采样率fs＝10 MHz。由于实际工程中VCO线性度做不到理想，故在多次测量中对目标距离和差频频率的理论关系作了修正，修正后的对应关系为：fi＝134．18 R＋13．4 k Hz。实测数据验证分析中的理论值也采用此修正关系。

图7给出了目标处于3．3 m时（理论差频频率为0．456 MHz）实测数据经ZFFT窗谱拟合后的结果。窗函数为汉明窗，抽取倍数为8，估计频率为0．466 MHz。

对比图2，可以很明显地看出经ZFFT窗谱拟合后能更好地找到实际目标对应差频信号频谱的最大值，其估计频率相比FFT和ZFFT更接近理论频率，从而更好地估计目标距离。

表1给出了此算法应用于该系统中对单一静止体目标在2～8 m距离内的实测数据与采用128点的FFT和抽取8倍后的ZFFT对比分析。在该应用中加窗类型为汉明窗，细化范围为FFT获得的距离谱的最大采样点和次大采样点之间，抽取倍数为8。该系统差频信号的采样样本点数为1 030，抽取倍数最大为8倍。

表1表明，在相同距离下，ZFFT细化8倍后，相对单一FFT估计误差明显减少最大估计误差由0．42 m减少到0．1 m，但是由于栅栏效应的存在，其找错谱线的概率依然存在，但经ZFFT窗谱拟合后，把ZFFT细化后的局部离散谱拟合为理论中的连续窗谱，在一定程度上减弱了栅栏效应，可更好地找到频谱最大值对应的频率，测距误差有了进一步的减少，普遍小于单一ZFFT的估计误差，其最大误差由ZFFT估计的0．1 m减少到0．05 m，测距精度提高了50%。

结合探测系统的实际应用，考虑目标运动带来的多普勒频移的影响，在其运动速度较低时，如多普勒频移为20 k Hz时，由于其带来的测距误差在最大估计误差范围内，可不考虑其影响。在目标运动速度较高，多普勒频移较大时，在系统参数的选择上，可提高调制频率的大小使其满足fm＞fd，来减少多普勒的影响；同时，由于本系统采用三角波调制，根据调制前后半周正负斜率的特点，可采用相加对消的方法，来消除多普勒频移的影响。

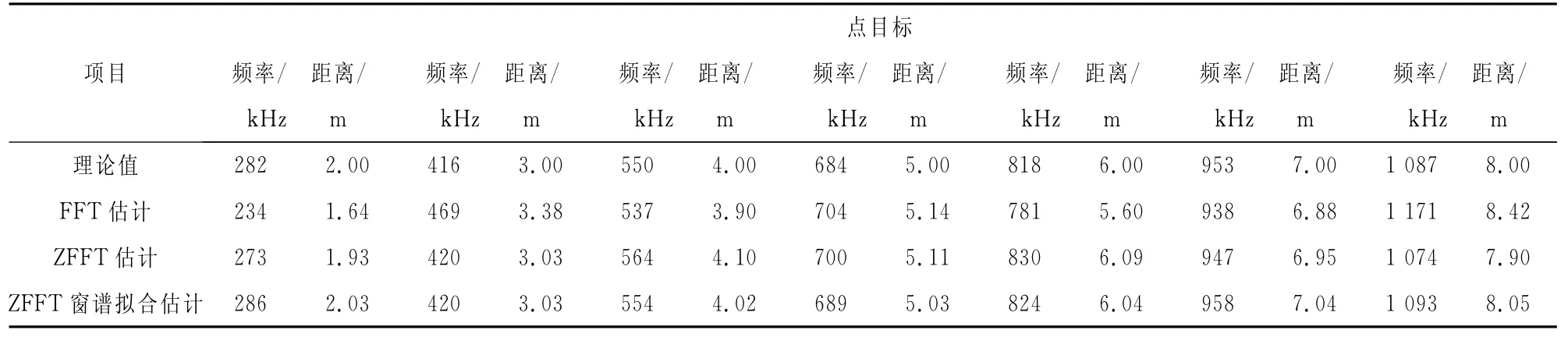
表1 实测数据FFT，ZFFT与ZFFT窗谱拟合估计结果Tab．1 Measured data FFT，ZFFTand ZFFT window Spectrum Fitting estimation

4 结论

对于毫米波调频探测系统的测距精度问题，本文提出了ZFFT窗谱拟合算法。在工程中采样数据一定，通过对差频信号进行加窗细化，再进行连续谱拟合估计，减少了细化倍数有限对频谱估计的影响，克服了栅栏效应，在计算量增加不多，满足探测系统实时性的情况下能更好地提高测距精度。实测数据结果显示了该算法比ZFFT能取得更好的效果。在实验验证中，由于系统采用对称三角波调制，目标运动带来的多普勒影响可通过正负对消的方法去除，从而转化为静止目标。对于其他调制系统，或对于多个复杂运动目标，需结合实际情况，做更进一步的研究。

［1］李兴国，李跃华．毫米波近感技术基础［M］．北京：北京理工大学出版社，2009．

［2］Kui Wang，Ran Tao，Tao Shan．Improved method of preweighed zoom FFT［C］／／9th international Conference on Signal Processing，2008．USA：Piscataway，NJ，IEEE：2008．

［3］丁康，潘成灏，李巍华．ZFFT与Chir p－Z变换细化选带的频谱分析对比［J］．振动工程，2001，14（1）：30－35．DING Kang，PAN Chenghao，LI Weihua．Spectr u m analysis comparison bet ween ZFFT and chir p－Z transfor m ［J］．Jour nal of Vibration and Shock，2001，14（1）：30－35．

［4］丁康，谢明，杨志坚．离散频谱分析校正理论与技术［M］．北京：科学出版社，2008．