基于累积差分的飞行测试数据同类段定义

艾冬生，张 珂，张 峰，卢一喆

（1．机电动态控制重点实验室，陕西 西安 710065；2．西安机电信息研究所，陕西 西安 710065）

0 引言

在现代飞行测试工程应用中，通常使用如遥测、外测等手段从不同的数据源获取海量数据，并通过专用的数据获取系统将数据存储于巨型文件中。飞行测试一般具有科目多、时间长等特点，测试过程中获取的多为海量数据。目前，针对海量飞行测试数据多采用高速计算机群进行处理。即使如此，在数据分析的过程中，在海量存储数据中查找满足特定条件的参数（例如查找参数P1≤13或是参数32≤P2≤40）仍会十分困难。

目前一般采用分段取平均的方法来处理上述问题，但在处理过程中会损失极值点的数据，导致段内有效数据信息的损失。针对上述不足，提出一种可适用于任意被测参数的基于累积差分的方法，用于定义参数P的同类段。

1 累积差分方法与同类段

1．1 累积差分方法

累积差分算法是一种简单且有效的针对同类数据段划分方法。它能在段内根据响应值及平均值得到累积差分的最大、最小边界曲线，其基本思想是：使用高斯分布模型来表征信号的概率分布，使用分段分割的方法将数据分段，在各段内使用一阶差分方程求得数据边界，并使用标准方差来断定数据的绝对偏移量，用平均值代替段内数据，从而降低数据量［1］。

如图1（a）所示为沿着x轴的3个独立段落和其对应的3个不同响应值（ri）。对段落中任意一点累积域Ax的计算，均可通过对响应函数沿着x轴进行积分获得：

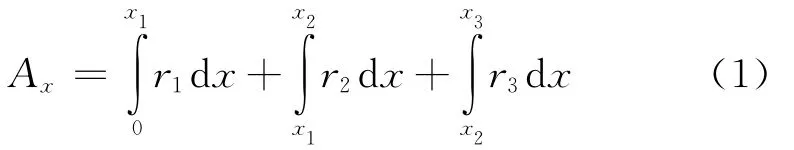
图1（b）所示为沿着x轴的响应值累积域，其中实线段为响应沿轴方向的累积域曲线，虚线段为响应平均值沿轴方向的累积域曲线。其中，实曲线的斜率变化反映了三个不同段落的响应值，虚线段的斜率反映了被积函数为沿着x轴响应变量累积域平均值时的情况。例如：∀x，如图1（b）所示，被积函数为响应函数的平均值时，累积积分域如下：

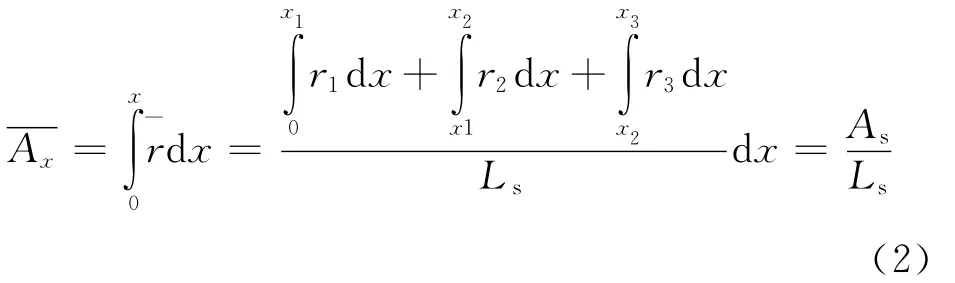
式（2）中，As为沿着x轴的累积域，Ls为段落长度。

图1 累积差分原理示意图Fig．1 Sketch map of cu mulative difference method

由式（2）可得，沿着x轴∀x的累积差分Zx可由式（3）表示：

式（3）中，Zx是实际值与平均值在 ∀x点的累积域值之差。如果将段落长度作为x轴，对应的累积差分Zx作为y轴，那么累积差分曲线斜率的正负变化的极值点位置就能够标识该段落的边界曲线。

1．2 飞行测试数据中的同类段

飞行测试应用中的被测参数多为缓变量，按照曲线斜率的正负变化极值对数据进行分段，用段内数据的平均值和标准方差作为因数［2］对同类段进行标识，这样对于原始飞行数据的存储就转化为对于包含同类段起始和结束边界值、范围内的平均值和标准方差等要素的数据存储。将这些要素作为索引存储于数据库中，会大幅提升数据检索速度，并且这一开销仅仅是存储所有数据开销的5%［3－4］。

2 基于累积差分的飞行测试数据定义同类数据段方法

在实际的飞行测试过程中，数据以帧为单位进行传输，对于等间隔采样的参数P，用于表征参数的存储数据可以被格式化为N 个点，记为N（ti，yi）（1≤i≤N），其中ti是数据采样起始时刻，yi是该时刻对应的值（yi是任意的实型数，如yi为非数据型，则用Na N予以标记），起始时刻t1和结束时刻tN用于标记段落长度。

计算格式化域中任意一点的累积域值Ax，那么基于N个格式化点得到N个累积域值，由此可以得到总区域和A，是累积域值Ax（1≤i≤N）的累加和。基于上述总区域和并结合段落长度（这里段落长度被本地化为起始时刻到结束时刻的时间长度），可计算出平均累积域值并代入式（3）可求得累加差分Zx。对于N个格式化点，可得出若干个Zx的值，累积差分曲线Zx随着斜率的代数符号发生变化时，将产生极大或极小值点，找出其极值点并将极值点所对应的ti时刻记录，由此可标识出各个段落的边界。

3 实例验证

下面以实际飞行测试中的取样数据来验证上述同类段定义方法，并对取样数据以取样时间进行段落划分。针对第一间隔距离数据段数据的计算，我们使用相邻间隔差分的计算方法，并通过将间隔距离起始点（或终止点）到当前点求累加来计算段落外的累积距离。对于间隔域的计算，可以通过式（2）用段落内的平均值乘以段落长度来获得，过程中采用统计平均的归一化公式将各段落值进行组合所得的结果作为段落内的平均值。统计量Zx由实测值Ax与其段落统计平均值AVG（Ax）做差得到。以实现线与虚线段中间的差分Zx为例（如图1（b）所示），其代数值由式（3）得到。

计算过程中将期望值与方差同时考虑，比单独使用期望值更加易于数据的统计分析，同时方差与标准差表明了数据点的置信水平，能够提升数据点的置信权重。将方差作为权值因子能够减小边界外数据点的影响，并能生成统计一致的归一化数值。如图2所示为实际测试数据应用累积差分算法给出的结果。可知，通过使用取值为2．85的标准差代替原始数据，从而使得在时间点为3．5时的峰值明显得到削减。

在完成累积差分计算后，采用用户自定义准则对均值进行运算，以进行统计相似段落的合并。图2示出了6 s样值区间中的几种同类段。可以看出，与使用原始样值（图中虚线所示）相比，使用段落划分能够有效压缩数据量，并且不损失原始数据信息。如果需要可将动态段落划分算法进行迭代使用，经过几次迭代计算，结果最终收敛于沿着控制域数据点的加权平均。

图2 实际测试样值数据的累积差分结果Fig．2 Conclusion of cu mulative difference according actual data

4 结论

本文提出基于累积差分的飞行测试数据中定义同类段的方法。该方法基于累积差分算法找出数据段中的极值点，由此确定同类段的边界。实例验证表明所述方法可用于定义飞行测试数据中的同类段。依据定义的同类段，计算出被测参数的统计数据（如平均值、标准方差等），采用统计值对原始存储数据进行替换，可在不损失数据信息的前提下有效压缩数据（对于二进制数据，压缩率为50%左右），并可根据同类段边界值对相关参数进行快速查找和处理。值得注意的是，在实际应用中，接收数据受传输信道误码影响会存在野值，可以在应用所述方法定义同类段之前将数据进行滤波处理，将数据中的奇异点去除或对数据进行平滑。

［1］Fridtjof Tho mas．Auto mated Road Seg mentation using a Bayesian Algorith m［J］．Journal of Transportation Engineering，2005，131（8）：591－598．

［2］Fridtjof Tho mas．Generating homogeneous road sections based on surface measurements：available methods［C］／／Proc．2nd European Pavement and Asset Management Conference．Ger many：Berlin，2004：21－23．

［3］Aashto．Guide f or Design of Pavement Str uctures［R］．A－merican Association of State Highway and Transportation Offices：Washington，DC，1986．

［4］Espeschit，Ant nio M．L，PENNA Sér gio D．A Web Search Engine to Flight Test Data［C］／／Proceedings of the 28th European Telemetry Conference．Ger many：Munique，2008：15－17 ．