多支点轴承同轴度和垂直度光学检测

朱 俊，韩春雷，谢仁富

(武汉第二船舶设计研究所，湖北 武汉 430064)

0 引言

用于支撑大型回转运动轴的多支点轴承系统，为了保证运动轴的回转精度，尽可能避免运动轴在回转时发生应力形变，各支点轴承必须具有很高的同轴度，同时要求运动轴的回转轴线相对基准面具有很高的垂直度。

根据同轴度的定义［1］，同轴度的公差带为一以基准轴线为轴线并包含被测要素轴线的圆柱体，圆柱体的直径即为同轴度。被测要素的轴线对基准轴线的同轴度误差由被测要素的轴线自身的直线误差、被测要素的轴线对基准轴线的偏离和被测要素的轴线对基准轴线的倾斜等3个部分组成。前者是由轴承零件本身的加工误差决定的，后两者则是由轴承系统的装调误差决定的。从工程实际来看，装调误差往往是主要的，是轴承系统同轴度误差的决定性因素。图1是2支点轴承系统同轴度误差简化模型示意图，两轴承的同轴度误差t=t1+t2，t1是两轴承轴线相对偏离量的情况，t2是两轴承轴线相对倾斜量及由角度量根据轴承间距折算而成的位移量。在轴承系统的同轴度测量和计算中，必须同时考虑轴承轴线对基准轴线的偏离量和倾斜量。

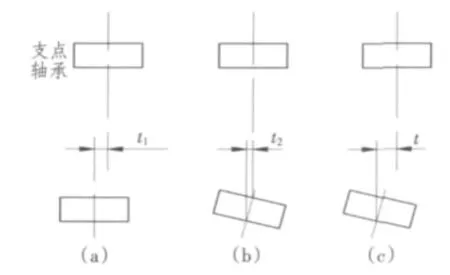
图1 同轴度装调误差简化模型Fig.1 Simplified model of coaxiality adjustment error

对大跨度长距离多支点轴承系统的同轴度及垂直度测量，传统的光学准直测量相对激光准直、激光干涉、光电成像等测量方法［2－4］具有稳定可靠、简便易行的特点。文献［5］详细讨论了同轴度光学检测方法、检测基准和同轴度装调控制要点，但其采用1台测微准直望远镜配合1台自准直光管进行测量，测量读数和数据处理都不考虑轴承轴线对基准轴线倾斜对同轴度的影响。本文采用2台测微准直望远镜相互准直测微，并提出根据读数计算出每个轴承轴线2个端点在测量坐标系中的坐标，求取各坐标点的拟合直线，即为各轴承的公共轴线，以此公共轴线作为计算同轴度的基准轴线，公共轴线对基准面的垂直度即为轴承系统的垂直度。最终计算结果同时包含了轴承轴线对基准轴线的偏离量和倾斜量。

1 检测原理和方法

1.1 光学准直测量原理

测微准直望远镜是用于光学准直测量的专用仪器，其光学系统主要由目镜、倒像镜、角度分划板、调焦镜、物镜、光学测微平板、位移分划板等组成。调节调焦镜可对45 cm到无限远聚焦。光学测微平板是用于测量微位移的重要部件，转动X，Y两个方向的测微鼓轮可分别带动测微平板在2个方向上转动，在鼓轮刻度盘上即可读出聚焦目标相对望远镜光轴的微位移量。位移分划板位于望远镜最前端，其中心在望远镜主光轴上，可以作为另1台望远镜的观测目标。

图2 2台测微准直望远镜相互准直测微Fig.2 Two micro alignment telescopes collimate each other

当2台望远镜相互瞄准对方位移分划板，如测微读数均为(0，0)，则表明2台望远镜主光轴重合。如光轴不重合，则可根据2望远镜测微读数计算出两光轴的位置关系，包括偏离量和倾斜量。以X方向为例，设望远镜A测望远镜B的位移分划板读数为dA，望远镜B测望远镜A位移分划板读数为dB，则望远镜B位移分划板中心偏离望远镜A光轴位移量为dA，望远镜B光轴与望远镜A光轴夹角

式中:L为2台望远镜位移分划板距离，需注意的是，通常θ为小角度，因此上式可以成立。

1.2 检测方法

利用测微准直望远镜测量轴承系统同轴度需要将望远镜临时安装到待测轴承的中心，以望远镜的光轴代替支点轴承的中心轴线。当测量精度要求很高时，通用的孔定心器难以满足定位精度，其固定方式也不够稳定，必须设计加工专用的定心轴，如图3所示。定心轴外圆与支点轴承内径相配和，内孔与望远镜镜管配合，并设计有专门的调整和锁紧机构。将望远镜和定心轴精密的装配起来，使定心轴外圆在标准V形块上转动，辅助定点参考目标，可将望远镜光轴与定心轴回转轴线调至很高的重合精度。此时将定心轴装入轴承，望远镜光轴即为待测轴承的中心轴线。在2个轴承中各装入1套带有准直望远镜的定心轴，互相瞄准测微，即可测出1轴承轴线相对另1条轴承轴线的偏离量和倾斜量。

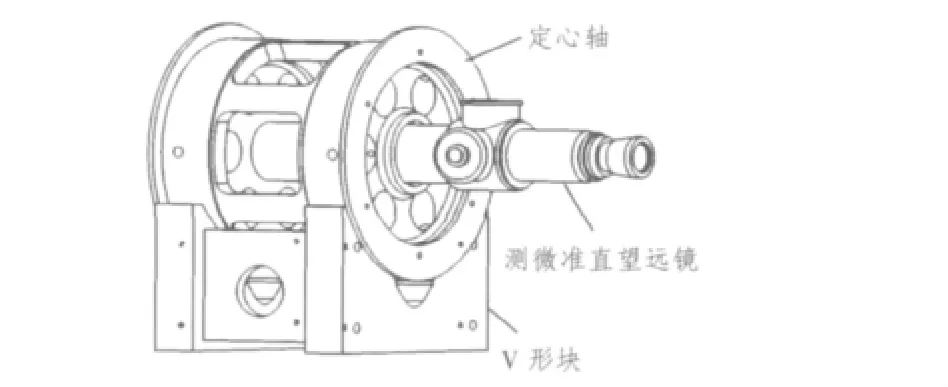
图3 精密检测工装Fig.3 Precise measuement assembly

但在实际应用时，按上述方法测量微位移，尤其在温湿度无法控制的恶劣环境中测量，常常出现读数变动较大的情况，每次装入定心轴测量的数据都会有较大的差别，甚至同一次装入定心轴，将定心轴在轴承内旋转1个角度，读数都可能发生很大的变化。这是因为在实际测量工程中，为了保证定心轴能装入轴承，定心轴外圆与轴承内孔需设计有一定的配合间隙，如0.02～0.05 mm。定心轴在轴承内转动时，望远镜光轴的位置并不固定，可能发生0.02～0.05 mm的跳动，虽然跳动量很小，但由于两轴承间距很大，从而给测量读数的结果带来很大的影响。

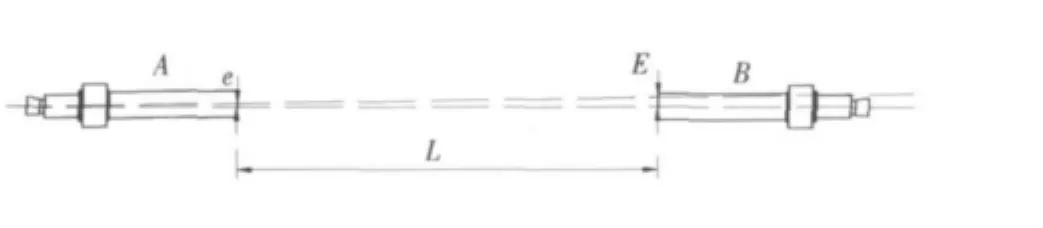
图4 配合间隙对测量的影响Fig.4 Influence of the fit clearance

如图4所示，通常情况下由于两轴承间距远大于轴承长度，当望远镜A的光轴发生微小变动量e时，望远镜A测望远镜B位移分划板的读数l和L分别是轴承长度和2个轴承的间距。例如，轴承长200 mm，2个轴承间距10 m，则望远镜读数相对实际偏移量e放大了50倍。由于定心轴与轴承内孔配合间隙的存在，间隙大小还受到温度影响，因此望远镜光轴的位置是不稳定的。若以某个望远镜光轴为计量基准，将很难得到稳定的观测数据。如果以此数据直接作为同轴度调整的依据，装调时无论如何调整，轴承系统同轴度可能也无法满足既定要求。因此，实际检测时应以各轴承的公共轴线作为同轴度的计量基准，检测方法如下:

测量前先调好仪器，将带有望远镜的定心轴装入待测轴承。以轴承系统某一侧的第1个轴承为测量时的基准轴承，装入其内的望远镜设为望远镜A，以垂直于望远镜A光轴的横切面为XoY平面，以望远镜A光轴为Z轴，建立测量坐标系，然后依次将望远镜B装入各个后续轴承，分别测量望远镜A与望远镜B之间的偏离量和倾斜量，根据轴承长度和各个后续轴承与基准轴承的间距，可以得到每个轴承轴线段2个端点在测量坐标系中的坐标，n个轴承可得到2n个坐标点，通过评价这2n个点的共线性来计算轴承系统的同轴度。虽然测量读数时是以某个轴承轴线为基准的，但计算同轴度时是以公共轴线作为计量的基准轴线，这样尽管每次测量读数受配合间隙影响可能相差较大，但最终的同轴度和垂直度计算结果是相对稳定的。同时，因为测量点包含了每个轴承轴线段的2个端点，因此既考虑了轴承偏离量也考虑了倾斜量对同轴度的影响。此外，通过计算公共轴线与轴承系统安装基准面的垂直度即可得到轴承系统的垂直度。

2 实验和数据处理

某三支点轴承支撑系统，1～3号轴承自上而下排列安装于垂直支架上，2号轴承、3号轴承与1号轴承的间距分别为 L12=1 m，L13=7 m，轴承长度l=200 mm，安装基准面为水准面。要求轴承系统装调同轴度不超过Φ0.2 mm，垂直度不超过30″。

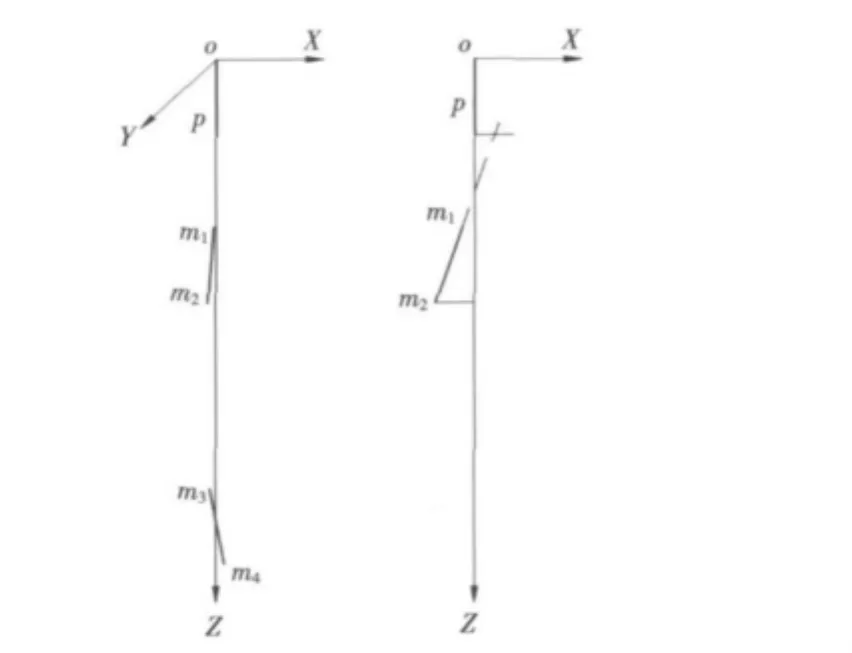
图5 测量示意图Fig.5 Measurement sketch

以最上方的1号轴承为测量基准，建立如图5所示的测量坐标系。图中线段op，m1m2，m3m4分别为各轴承轴线，测量时即为望远镜光轴。通过依次测量读数可得到6个测量点在坐标系XYZ中的坐标。显然，o，p 两点坐标分别为(0，0，0)、(0，0，l)。其余各点坐标通过望远镜测微读数计算得到。以点m1，m2在XZ面内的坐标计算为例，1号轴承望远镜测2号轴承望远镜位移分划板读数记为d12，2号轴承望远镜测1号轴承望远镜位移分划板读数记为d21，依此类推，读数应按统一的方向约定正负号。根据图5所示的位置关系可得m1和m2坐标:

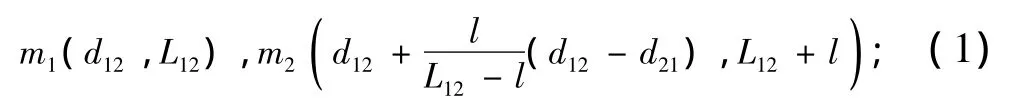
同理可得:

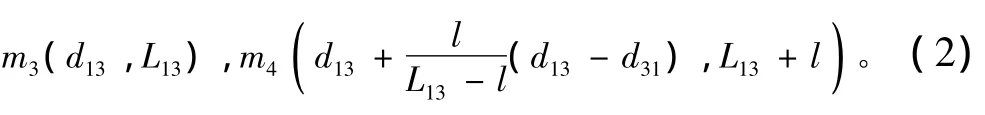
各点Y坐标的计算与上述方法完全相同。

得到6个点的坐标后，通过空间直线拟合求取3个轴承的公共轴线。空间直线方程可表示为:

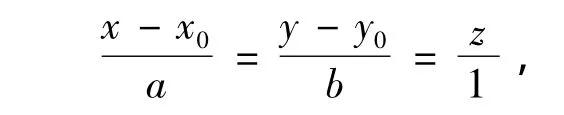
上式等价于

将方程组写为矩阵形式

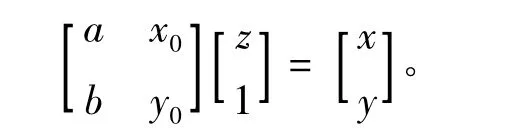
将n个测量数据点的坐标(xi，yi，zi)，i=1 ～ n带入上式可得

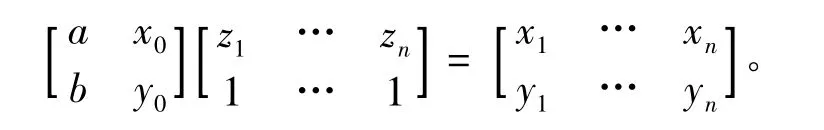
根据最小二乘法拟合得到

由上式可以解出拟合直线方程的系数:

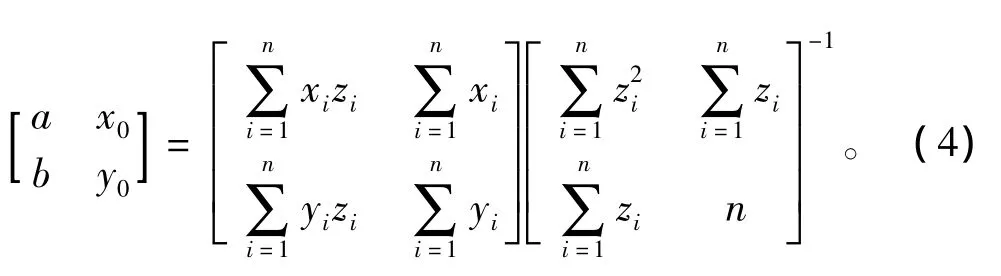
将测量数据点的坐标带入式(4)即可得到拟合直线方程。

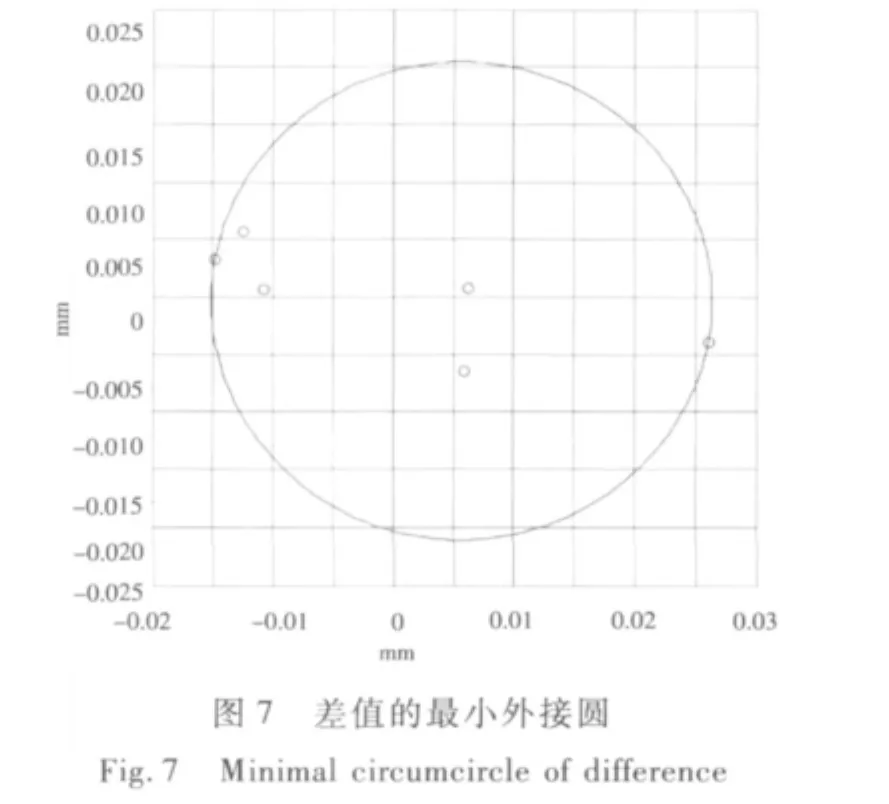
根据直线方程(3)可计算每个测量点的在X，Y方向的真值xia，yia，并求出相应的差值，

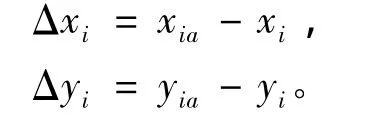
(Δxi，Δyi)的最小外接圆直径即为轴承系统的同轴度［6］。

表1是对三支点轴承系统某1次测量的原始读数，表2为数据处理计算结果，根据表2的计算结果求得的最小外接圆直径为0.04 mm，此数据即为轴承系统的同轴度。

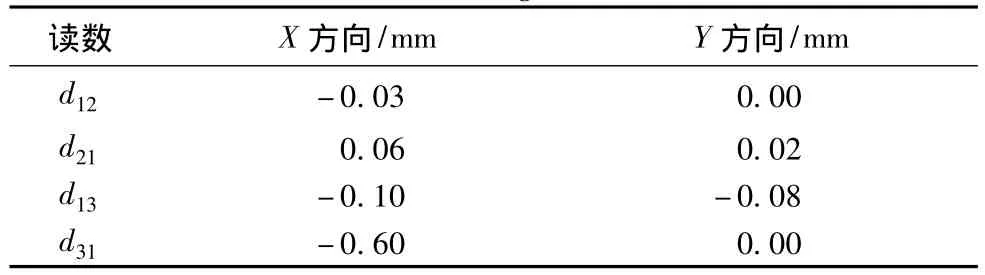
表1 原始数据Tab.1 Original data

表2 计算数据Tab.2 Calculated data

该轴承系统安装基准为水准面，为了检测轴承系统垂直度，可在1号轴承望远镜下方架设垂准镜或水银面，采用自准直测量法或自动反射测量法测出望远镜光轴对水准面的垂直度。1号轴承望远镜光轴即测量坐标系Z轴，只要计算出公共轴线与Z轴的夹角即可求得公共轴线对水准面的垂直度，即为轴承系统的垂直度。

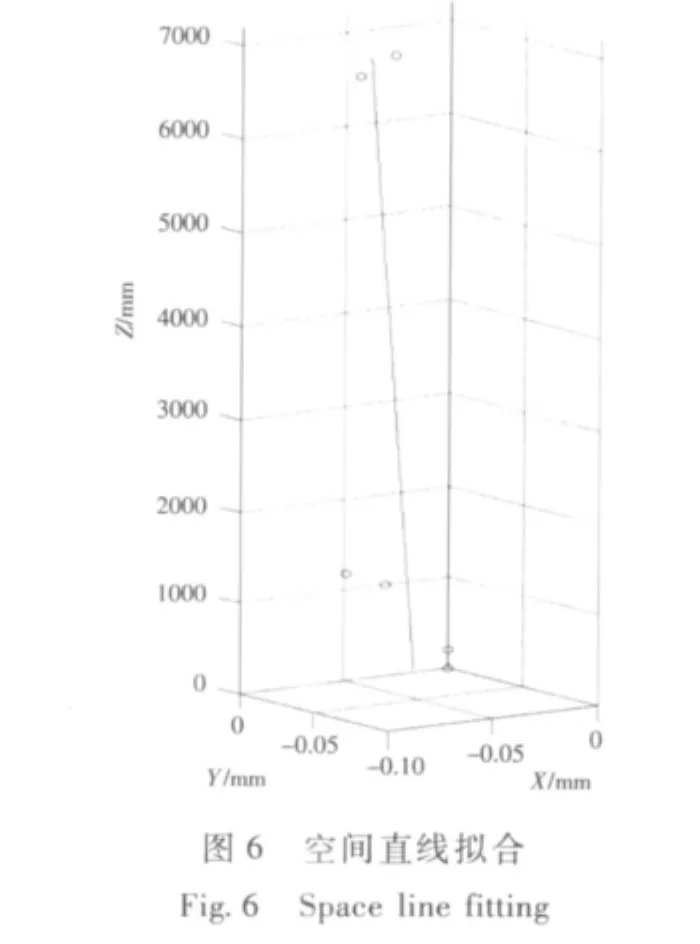
实测1号轴承望远镜光轴对水准面垂直度为(－0.06，－0.05)mm/m，计算公共轴线与Z轴夹角为(－0.012，－0.012)mm/m，计算轴承系统垂直度为(－0.072，－0.005)mm/m，换算成角度为19.6″。

在实际测量时，为了进一步提高检测数据的可靠性，尽可能减小定心轴与轴承间隙对同轴度检测的影响，还可将定心轴在轴承内转动一个角度，重复上面的测量和计算过程。典型的做法是每间隔90°测量1次，转动1周测量4次，n个支点的轴承系统可以获得4n组测量数据，如果每组数据计算出的同轴度和垂直度结果都在规定的公差范围内，表明轴承系统装调很好地满足要求。

3 结语

以各个支点轴承的公共轴线作为计算多支点轴承系统同轴度和垂直度的基准轴线，可以避免定心轴与轴承间隙对测量读数的影响，获得相对稳定的同轴度数据。公共轴线是通过对各个轴承轴线端点作空间直线拟合计算得到的。由于光学检测方法采用2台测微准直望远镜相互准直测微位移，这样可以获得每个轴承轴线段2个端点在测量坐标系中的坐标值，因此在直线拟合结果中既反映了各轴承轴线对公共轴线的偏离，也反映了各轴承轴线对公共轴线的倾斜。实验和数据处理结果表明上述方法在大型的多支点轴承系统同轴度、垂直度检测中稳定、可靠、精度高，具有广泛的工程应用价值。

［1］GB/T 1182-2008，产品几何技术规范(GPS)几何公差形状、方向、位置和跳动公差标注［S］.

［2］LU Nai-guang，DEN Wen-yi，YAN Bi-xi.et al.Laseralignment system used for coaxiality measurement of large scale holes［J］.SPIE，2000，(4222):383 －386.

［3］成相印，方仲彦，殷纯永，等.长距离同轴度测量方法及实验［J］.计量学报，1997，18(2):85 －89.CHENG Xiang-yin，FANG Zhong-yan，YIN Chun-yong，et al.Long distance coaxiality measurement system and experiments［J］.Acta Metrologica Sinica，1997，18(2):85 －89.

［4］汪亭玉.船舶柴油机主轴承同轴度测量系统误差分析［J］.船海工程，2008，37(2):59 －61.WANG Ting-yu.Error analysis of coaxiality measurement system for bearings of crank shaft of marine diesel engine［J］.Ship ＆ Ocean Engineering，2008，37(2):59 －61.

［5］宫经汉，陈琳.多支点同轴度检测方法研究［J］.舰船科学技术，2004，26(5):57 －60.GONG Jing-han，CHEN Lin.Testing method research of multi-pivot coaxiality［J］.Ship Sience and Technology，2004，26(5):57 －60.

［6］张镭，张玉.同轴度误差的解析评定法与仿真研究［J］.计量学报，1997，18(1):32 －37.ZHANG Lei，ZHANG YU.Analytic evaluation of coaxiality error and computer limitation research［J］.Acta Metrologica Sinica，1997，18(1):32 －37.