RBF神经网络的行车路径代价函数建模

陈亮，何为，韩力群

(北京工商大学计算机与信息工程学院，北京 100048)

RBF神经网络的行车路径代价函数建模

陈亮，何为，韩力群

(北京工商大学计算机与信息工程学院，北京 100048)

行车路线优化是城市智能交通系统的研究热点之一，对整个交通系统的优化起着重要作用.分析了影响行车时间的各种因素，结合图论中最短路径算法，建立了基于RBF神经网络的路径代价函数模型.基于该函数模型，可以计算出交通图中任意给定两地间的时间最优路径.将该模型应用于实际路况进行有效性验证，得到了有实用价值的结果，说明了该模型的正确性和有效性.

智能交通;路径代价函数;行车路线优化;RBF神经网络;图论

在城市智能交通系统中，行车路线优化对整个交通系统的优化起着重要作用，选取最优车辆行车路线，可以加快车流速度，减少拥堵发生，还能减少因为堵车而造成的交通车辆刮蹭等事故的概率，因此，该课题的研究具有重要的实用意义.

行车路线优化属于路径优化问题.目前关于路径优化的研究主要集中在如何找到最短路径，其中常见的一类方法是采用图论中的Dijkstra算法，具体实现算法有 A－star［1］、Bellman、Ford2Moore、Floyd 等［2］;另一类常用方法是基于蚁群算法的解决方法，如2007年Horoba等人提出的基于随机过程的改进蚁群算法最短路径寻优［3］，2009年Punyaslok提出的多网络流最优化框架，2010年Zakzouk提出的基于蚁群算法利用模糊约束解决最短路径问题［4］.

道路交通网络的实际情况非常复杂，每个路段的行车时间除了与距离有关外，还与路宽、路况、气候及行车时段等诸多因素相关，因此最短路径并不意味着最短行车时间，不能简单地用路径长度计算路径的代价值［5］.鉴于此，本文从实际情况出发，综合考虑了各种影响行车时间的主要因素，建立了较为实用的路段代价函数模型并进行了实验验证.

1 路径代价函数及其影响因素分析

图论中每个弧段都可用其代价函数值表示，2个给定点之间的路径代价函数值则可用构成该路径的所有弧段的代价函数值之和表示.2个给定点间的最优路径即指所有可达路线中代价函数值最小的路径［6］.

实际应用中，弧段对应于两相邻路口之间的路段，路径对应于出发地到目的地之间的行车路线，代价函数值则对应于行车时间代价.实际道路中，很多因素都会影响车辆通过路段的时间，表1列出了可能影响车辆通过路段时间的主要因素［7］.

表1 车辆通行时间的影响因素Table 1 The influencing factors of vehicle travel time

在诸影响因素中，可进一步筛选出相互独立的主要因素.经过深入调研，本文确定了5个相互独立的影响因素:实时交通路况、车道数(路宽)、道路长度、自助红绿灯数量以及车辆转向.

2 基于RBF网络的路段代价函数建模

在实际道路中，车辆通过路段的时间与其影响因素之间存在着严重的非线性和不确定性，因此很难用解析式来表达.人工神经网络适于处理非线性问题，利用神经网络建立路径代价函数模型，是一种可行的途径［8］.适合拟合非线性关系的神经网络主要有BP网络和RBF网络，经实验对比，采用效果较好的RBF网络进行建模［9］.

2.1 基于正交实验的训练集设计

RBF网络的输入是影响车辆通行时间的因素，教师信号是车辆通过路段的实际时间.本文所确定的影响因素包括:实时路况x1、车道数量x2、行人自助式红绿灯数量x3、路段长度x4、车辆在路口的转向方式x5.

可以看出，上述影响因素既有语言变量，又有数值变量.首先，对各影响因素进行数值化和离散化.其中:x1为语言变量，根据北京市交通管理局现有标准划分，共分为3种路况:“畅通”、“缓行”、“拥堵”，与3个语言值对应，x1取值分别为0、1、2;x2可直接采用实际车道数，分为1～2条、3条、4条3种情况，x2取值分别对应为0、1、2;行人自助式红绿灯数量x3，可直接采用实际数量，取值分别为0、1、2.路段长度x4可离散为3个区间，分别为小于500 m、500 ～1 000 m、大于1 000 m，对应的x4取值为0、1、2;x5也是语言变量，可分为“直行”、“左转、“右转”3 种情况［10］，分别用 0、1、2 表示.按照上述规定，5种影响因素的完全搭配可产生243个样本对，而每个样本对中的教师信号必须来自与输入条件相符的实际情况.为了减少工作量，采用正交实验设计法来构造样本集，其优点是:正交表能在保证采集数据均匀分布的前提下，大大减少训练网络所需的样本数.本文将每个影响因素分成3个水平，如表2所示.表2给出了水平因素表，x1～x5是对道路通行时间不同的影响因素，再将每一个影响因素具有的3个水平填入表中.

采用的正交试验如表3所示.将5个不同因素的不同水平分别排列组合得到的18种实验组合情况.虽然只给出了18种实验组合情况，但是用这个表设计的训练集保证了实验数据的代表性.

2.2 基于RBF网络的路段代价函数建模

由于采集到的输入输出数据取值范围差别很大，需进行归一化处理，将输入数据归一化到［－1，1］区间，教师信号的时间单位采用小时，归一化到(0，1］区间［11］.数据归一化后的情况如表 4 所示.

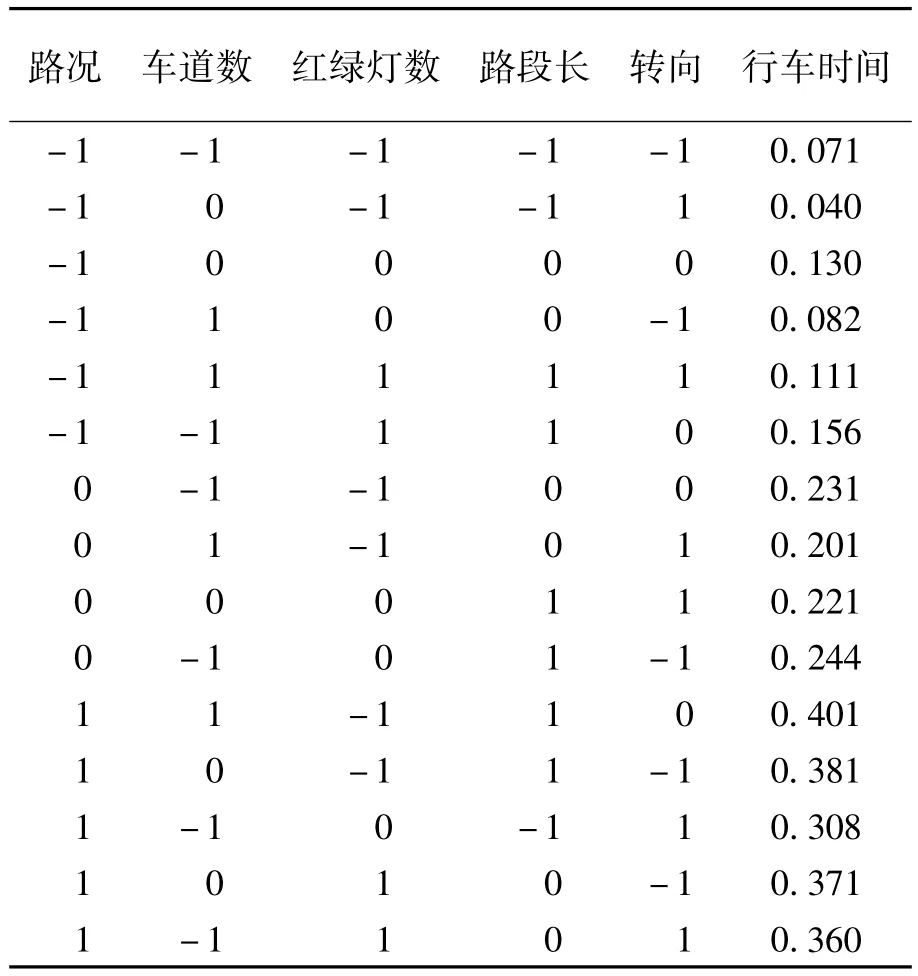
表4 数据归一化Table 4 Data normalization

表4根据x1～x5这5个影响行车时间因素的实际情况，依据表3，然后分别将其归一化，如x1～x4归一化的原则是本身对应的3个水平，将其归一化至［－1，0，1］，x5是时间，将其归一化至［0，1］.

RBF网络的设计与训练采用函数net=newrb(P，T，goal，spread)，其中，P 为 5 维输入向量，T为网络输出的行车代价值，训练误差目标值goal设定为0.01，spread为径向基函数的扩展系数，经调试取为 1.5［12］.

2.3 模型验证

由于特定路段的行车时间具有不确定性，采用上述方法建立的路段代价函数其输出并非准确的行车时间，而是行车代价值，其作用是通过比较不同可达路线的行车代价从而确定最优行车路线.本文用表5中的15组实际数据对模型进行验证，结果如表5的第7列所示.

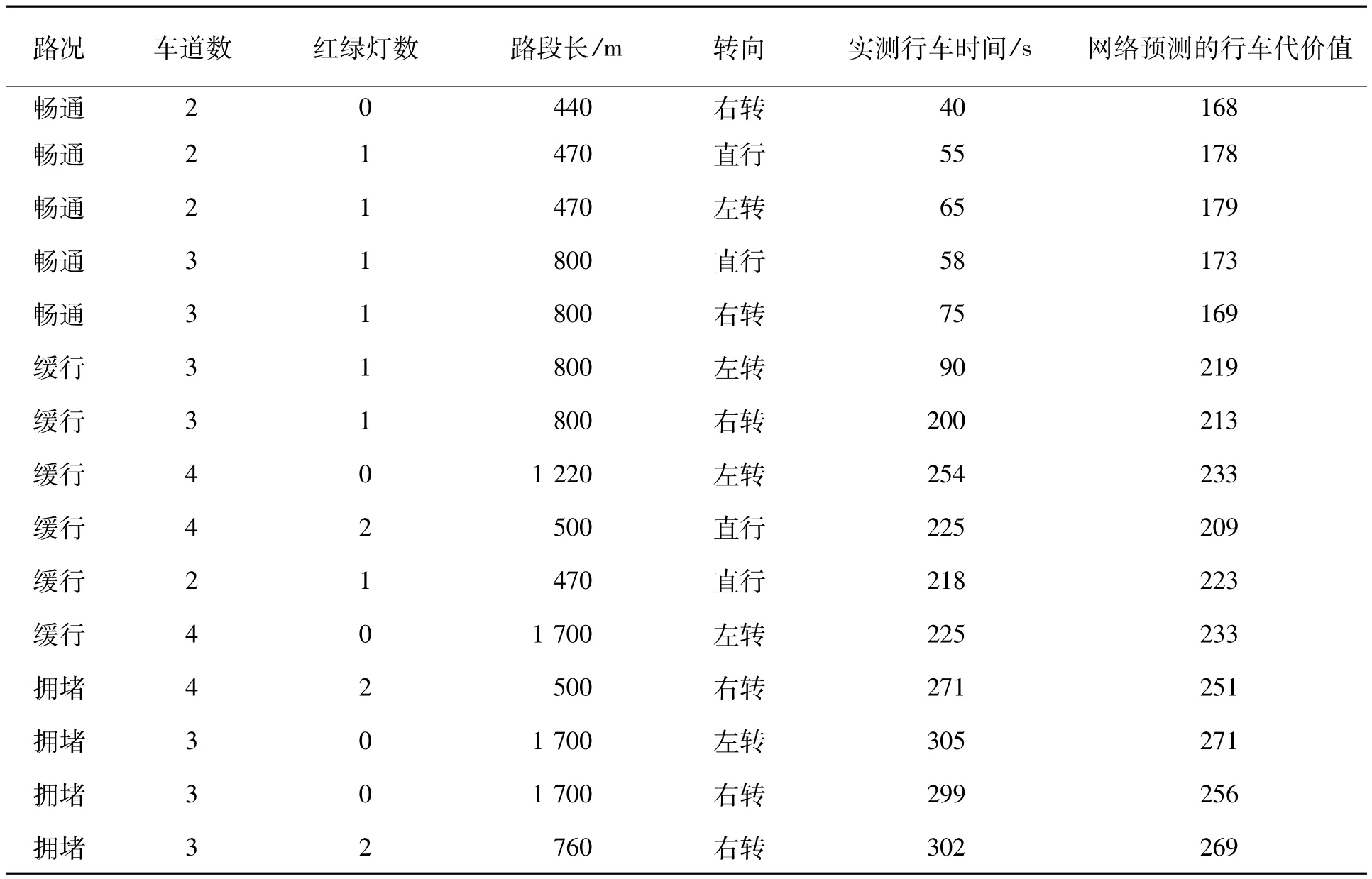
表5 仿真结果对比Table 5 Simulation results comparison

从表5可知，拥堵路段的网络预测代价值要明显大于畅通与缓行的值，说明实际道路路况是影响车辆行驶时间的主要因素，当其他因素相同时，转向会影响所用的时间，如左转比直行和右转花费的时间都多，这与日常常识是相符的.5个影响因素中的x1、x3、x4都是正向关因素，即水平越高，所花费时间越长，网络的预测值同样也越大，而x2是反相关因素.仿真结果如图1所示，同样也可以看出，神经网络的仿真预测结果与实测结果趋势一致，表明所设计的路段行车代价函数模型可靠.图1中需要说明的是，实际行车路线是以秒为单位计时，而神经网络计算的行车代价值没有单位，不表示实际消耗的时间，表示的是车辆行驶在不同的路段所耗费时间多少的横向比较，并以此为依据，最终选择出最优路径.

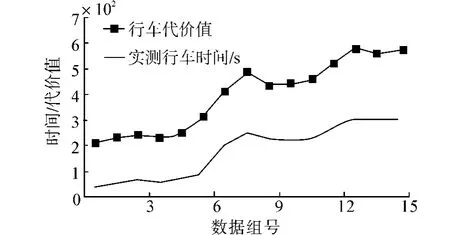
图1 仿真值与实际测量值Fig.1 Simulation and test values

3 应用实例

3.1 应用实例概述

本文应用实例是利用路段代价函数模型确定特定路况条件下，从航天桥至西单路口的最优路线，实际道路如图2.具体步骤是:首先将交通网络图抽象成为加权有向图［13］，找出连通起点和终点的所有可达路线，2个相邻交通路口之间是一个路段，从而可将各可达路线表示为一个路段系列，其中每个路段的实际情况可用一个5维向量进行描述，代入路段代价函数模型后可计算出该路段的行车代价值，所有路段的代价值之和即为路径的行车代价值，其中行车代价值最小的路径为最优路径［14］.

图2 实际交通道路Fig.2 Actual traffic roads

可达路径的搜索方法如下.

1)将图2中的交通图抽象为加权有向图，对不能提供实时路况信息的路段视为不可达，从而得到图3.图3中，1号节点为航天桥，15号节点为西单路口.

2)建立加权有向图的邻接矩阵.

3)根据邻接矩阵，从起始点开始找出下一节点;若下一个节点等于目标点，则返回2).

4)将起点到终点经过的全部节点串连起来，形成完整路径，将路径中经过点的权值相加，得到整条路径的权值［15］.

根据上述算法共得到92条可达路线［16］，略去情况近似的路径，选出差别较大的20条路径，根据距离长短对可达路线编号，如表6所示.

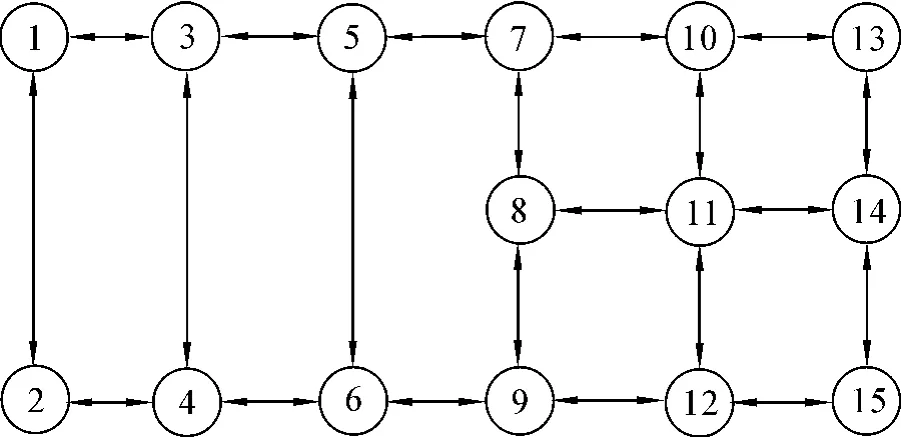
图3 加权有向图Fig.3 Weighted directed graph

表6 均匀抽出20条可达路线Table 6 Uniform extraction 20 paths

续表6

表6为所有可达路径中均匀抽取出的20条可达路径，按实际距离从小到大排序，可知，最短可达路线的距离为6.55 km，最长可达路线的距离为14.45 km.

3.2 确定最优行车路线

图4给出了早上7:00时上述路段的实时路况交通图，其中细线路段为畅通，粗线路段为缓行，粗虚线路段为拥堵.

结合图4中实际的交通路况，并利用路段行车代价函数模型计算表6中各可达路线的行车代价值，将得到的行车代价值从小到大排序，结果如表7所示.

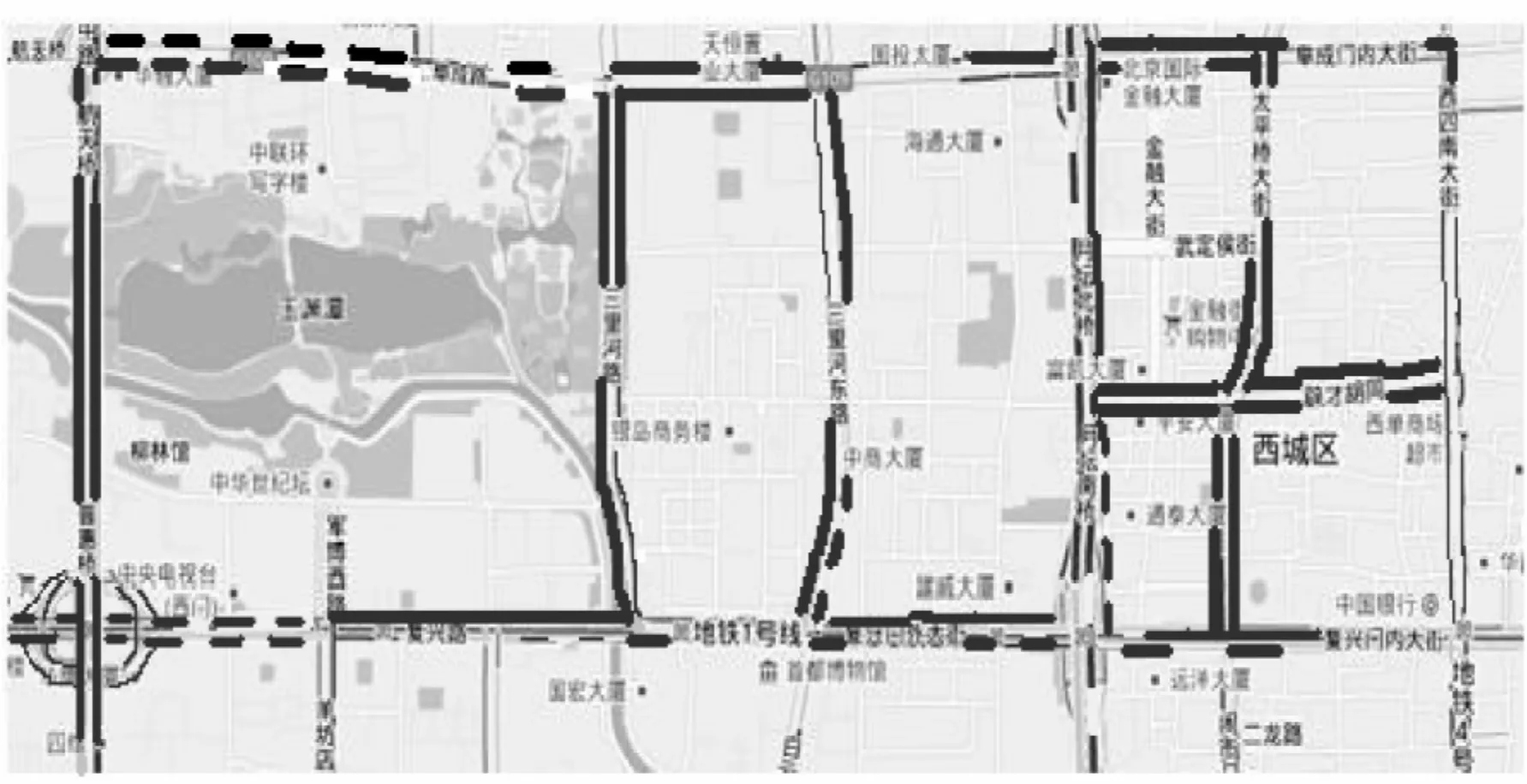
图4 实时交通路况Fig.4 Real time traffic

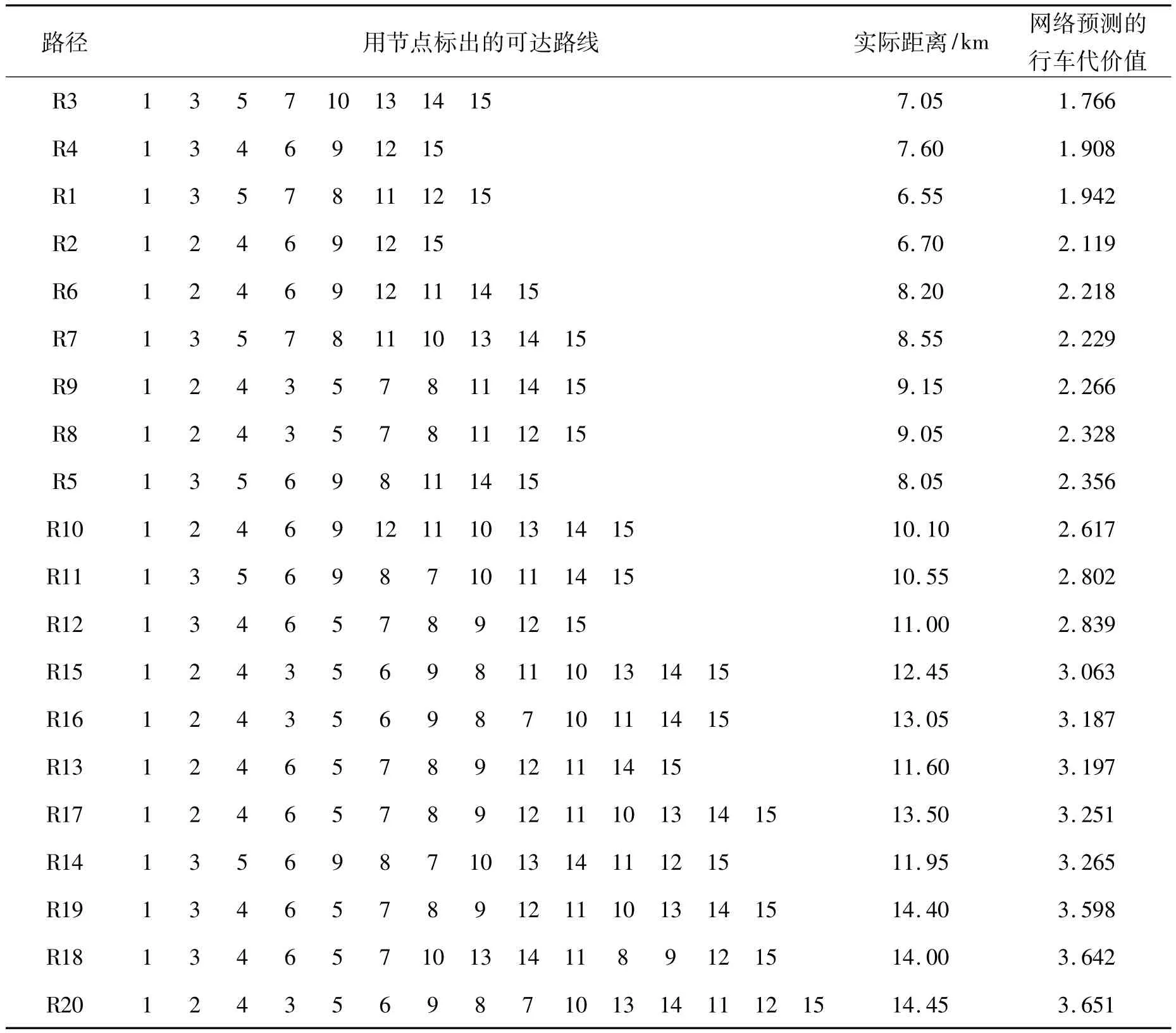
表7 最优路径排序Table 7 Optimal paths sort

从表7中可以看出，根据行车代价函数模型选出的最优路径R3并非距离最短的路径R1，虽然多走了500 m的路，但却有效地避开了拥堵路段，节约的时间大于绕路的时间代价.

3.3 可达路线生成算法的改进

根据上述算法共得到92条可达路线，其中很多“绕路”的情况不符合常识，如表7中的R20.一种改进的思路是，在计算可达路线时增加约束条件［17］.例如，按照“不走回头路”的要求，每个节点的选择方向必须与终点的2个方向分量一致，按照这样的条件，本例共选出9条长度近似的可达路线［18］，表8中列出了这9条可达路线的行车代价预测值.

表8 改进算法后的最优路径Table 8 Optimal paths by the improved algorithm

从表8可以看出，附加限制条件后，选出的可达路线即距离最短的前9条路径，当加上约束条件对最优路径的选择会产生一定影响，但却大大提高了计算效率，并能保证行车时间和距离双优化.可以看出，表8中的改进路径IR9和表7中的路径R3相同.

在根据常识设计约束条件时，也可考虑允许在某一个方向上“绕行”.例如，起点到终点在东西方向上的距离比南北方向的距离长，通常人们会选择在东西方向少走回头路，在南北方向上可视路况适当绕行，反之亦然.本例中，东西方向距离比南北方向距离长，当设定禁止向西行驶的约束条件时，得到的可达路线数为72;若附加条件为禁止向北行驶，则可达路线数为12.

3.4 有效性验证

本文从表7中选取R1、R3和R9 3条路径，请3位志愿者同时开车从航天桥出发，分别按照规定的路径前往西单，并记下行程时间.结果是:R9的行车时间为41 min，R1的行车时间为52 min，R3的行车时间为66 min.可以得出，RBF行车代价函数模型给出的行车路线排序与实际情况相同.

4 结束语

本文的特点是利用RBF神经网络建立最优路径代价函数模型，通过图论中的算法找到起点和终点的时间最优路径.在设计神经网络模型过程中，训练集的设计由正交实验法给出，训练出的网络模型测试结果较好，最后将模型应用到实例中，从最优路径代价函数模型给出的最优路径排序中选取差异较大的3条路径，经实际验证取得了较好结果.本次研究的不足在于，诸如天气因素(风、雨、雪、雾4类天气)并没有加入到网络的训练集中，原因在于这些因素在研究过程中较难采集，在以后的时间范围内将继续观察采集并加入这些因素的数据，将神经网络的训练集丰富完善，使其能够更加真实地反映出交通网络路径的代价函数值，更加贴近实际情况.

［1］张渭军，王华.城市道路最短路径的Dijkstra算法优化［J］.长安大学学报:自然科学版，2005，25(6):62－65.

ZHANG Weijun，WANG Hua.Optimation Dijkstra arithmetic for shortest path of urban traffic net［J］.Journal of Chang’an University:Natural Science Edition，2005，25(6):62－65.

［2］姜桂艳，郑祖舵.基于记忆机制的动态交通路径优化算法［J］.吉林大学学报:工学版，2007，37(5):1043－1048.

JIANG Guiyan，ZHENG Zuduo.Dynamic traffic path optimization algorithm based on mnemonic mechanism［J］.Journal of Jilin University:Engineering and Technology Edition，2007，37(5):1043－1048.

［3］HOROBA C，SUDHOLT D.Ant colony optimization for stochastic shortest path problems［C］//Proceedings of the 12th Annual Genetic and Evolutionary Computation Conference.New York，USA:ACM，2008:1465－1472.

［4］ZAKZOUK A A A，ZAHER H M，EL－DEEN R A Z.An ant colony optimization approach for solving shortest path problem with fuzzy constraints［C］//2010 The 7th International Conference on Informatics and Systems.Cairo，E－gypt，2010:1201－1208.

［5］王泉啸，蔡先华.动态最佳路径算法研究［J］.城市勘测，2009，73(1):73－75.

WANG Quanxiao，CAI Xianhua.Study on the algorithm of dynamic optimal route［J］.Urban Geotechnical Investigation＆ Surveying，2009，73(1):73－75.

［6］徐俊明.图论及其应用［M］.3版.合肥:中国科学技术大学出版社，2010:21－53.

［7］刘海燕.智能交通系统的车辆行驶最佳路径算法［J］.北京工商大学学报:自然科学版，2006，24(1):53－55.

LIU Haiyan.Best running path arithmetic of vehicles in intelligent transport system［J］.Journal of Beijing Technology and Business University:Natural Science Edition，2006，24(1):53－55.

［8］韩力群.人工神经网络教程［M］.北京:北京邮电大学出版社，2006:127－143.

［9］马君，刘晓东，孟颖.基于神经网络的城市交通流预测研究［J］.电子学报，2009，37(5):1092－1094.

MA Jun，LIU Xiaodong，MENG Ying.Research of urban traffic flow forecasting based on neural network［J］.Acta Electronica Sinica，2009，37(5):1092－1094.

［10］朱文兴，贾磊，丁绪东，等.城市交通网络中的路径优化研究［J］.山东大学学报:工学版，2005，35(1):74－77.

ZHU Wenxing，JIA Lei，DING Xudong，et al.Research on the route optimization in urban traffic network［J］.Journal of Shandong University: Engineering Science，2005，35(1):74－77.

［11］韩力群.人工神经网络理论、设计及应用［M］.2版.北京:化学工业出版社，2007:164－191.

［12］傅荟璇，赵红.MATLAB神经网络应用设计［M］.北京:机械工业出版社，2010:62－63.

［13］刘张雷，史忠科.城市动态时间最短路径诱导系统实现研究［J］.控制工程，2010，17(3):351－355.

LIU Zhanglei，SHI Zhongke.Implementation of urban tmie－dependent shortest route guidance system［J］.Control Engineering of China，2010，17(3):351－355.

［14］罗嵩，王坚.智能交通系统的最优路径搜索算法的研究与实现［J］.机电产品开发与创新，2008，21(2):10－12.

LUO Song，WANG Jian.Optimal path search study and practice based on the intelligent transportation systems［J］.Development and Innovation of Machinery and Electrical Products，2008，21(2):10－12.

［15］PETTIE S，RAMACHANDRA V.A shortest path algorithm for real－weighted undirected graphs［J］.SIAM Journal of Computing，2005，34(6):1398－1427.

［16］王海英，黄强，李传涛，等.图论算法及其MATLAB实现［M］.北京:北京航空航天大学出版社，2010:12－18.

［17］王晓丽，杨兆升，吕旭涛，等.平行四边形限制最短路径算法及其在交通网络中的应用［J］.吉林大学学报:工学版，2006，36(1):123－127.

WANG Xiaoli，YANG Zhaosheng，LV Xutao.Shortest path algorithm based on limiting parallelogram［J］.Journal of Jilin University:Engineering and Technology Edition，2006，36(1):123－127.

［18］魏二虎，贾满，李林燕.最短路径算法的改进方法研究［J］.测绘信息与工程，2007，32(4):40－42.

WEI Erhu，JIA Man，LI Linyan.On improvements for shortest path algorithm［J］.Journal of Geomatics，2007，32(4):40－42.

陈亮，男，1986年生，硕士研究生，主要研究方向为人工神经网络、智能交通.

何为，男，1953年生，高级工程师，IEEE会员，中国人工智能学会理事、智能产品与产业工作委员会秘书长，中国计量测试学会高级会员.主要研究方向为非电量检测技术、计算机测控技术、嵌入式技术应用，主持或参与国家科技攻关、火炬计划、省部级、横向等各类科研项目30余项，发表学术论文30余篇，获国家发明专利3项.

韩力群，女，1953年生，教授，中国人工智能学会副理事长.主要研究方向为智能信息处理与图像工程技术，主持各类科研项目30余项，获国家发明专利3项、北京发明创新大赛银奖1项.发表学术论文120余篇，出版专著10部.

Radial basis function neural network modeling of the traffic path cost function

CHEN Liang，HE Wei，HAN Liqun
(College of Computer and Information Engineering，Beijing Commercial and Industrial University，Beijing 100048，China)

Vehicle route optimization is one of the hot topics in research on urban intelligent transportation systems(ITS)，and it plays an important role in the optimization of the entire transportation system.This paper analyzed various factors that affect the travel time and established a path cost function model with an radial basis function neural network，based on the shortest paths algorithms in graph theory.By this function model，the time－oriented optimal path between any two given places on a traffic map can be calculated.The model was applied to actual traffic to validate the effectiveness，and its results are of practical value，showing the correctness and validity of the model.

intelligent transportation;path cost function;vehicle route optimization;radial basis function neural network;graph theory

TP391.4

A

1673－4785(2011)05－0424－08

10.3969/j.issn.1673－4785.2011.05.006

2011－04－22.

陈亮.E－mail:newboy_01@163.com.