高斯过程及其在高光谱图像分类中的应用

姚伏天，钱沄涛

(1.浙江大学计算机学院，浙江杭州 310027;2.浙江大学人工智能研究所，浙江 杭州 310027)

高斯过程及其在高光谱图像分类中的应用

姚伏天1，2，钱沄涛1，2

(1.浙江大学计算机学院，浙江杭州 310027;2.浙江大学人工智能研究所，浙江 杭州 310027)

高光谱遥感图像分类是高光谱成像信息处理的研究热点，高光谱成像的内在特点对于分类器设计具有直接影响.高斯过程是近年来发展迅速的一种新的机器学习方法，具备容易实现、超参数可自适应获取以及预测输出具有概率意义等优点，比较适合于处理图像分类问题.首先对高斯过程的基本概念及其主要的分类算法进行了简要介绍，然后在对高光谱图像分类的特点和高光谱图像分类的研究现状的分析基础上，讨论了基于高斯过程的高光谱图像分类的基本思想，提出了基于空间约束的高斯过程分类和基于半监督高斯过程分类等适合高光谱图像分类的新方法.最后对基于高斯过程的高光谱图像分类研究的发展趋势进行了展望.

高斯过程;高光谱图像;机器学习;图像分类

高斯过程(Gaussian process，GP)是近几年发展起来的一种机器学习技术，是目前国际上机器学习研究的热点领域，常被成功应用于处理回归与分类问题.与人工神经网络(artificial neural network，ANN)和支持向量机(support vector machine，SVM)相比，GP的突出优点是在不牺牲性能的条件下容易实现，其超参数可在模型构建过程中自适应获得，具有严格的统计基础，并且其预测输出具有清晰的概率解释.

GP预测的思想可以追溯到20世纪40年代［1］.众所周知，GP预测在地理统计学中被称为 Kriging［2－3］.Thompson［4］和 Daley［5］将其引入气象学中，Whittle［6］将该方法用于空间预测，Ripley［7］和 Cressie［8］将GP预测用于空间统计.随后人们逐渐意识到GP预测可用于通用回归问题，文献［9－11］中将GP用于计算机实验数据分析，文献［12－13］基于机器学习理论重新描述了GP回归和分类.

基于GP的分类器设计近年来受到越来越多的关注［14－16］.分类问题定义为给定输入向量 x，通过预测概率值P(c|x)来给输入向量x指定类别c.传统分类方法中，分类面由一组加权基函数组合而成，通过训练数据求得每个基函数的系数，从而确定分类面;但是，对于高维数据，因基函数和待求系数过多，易引起过拟合问题.由于GP不是将约束加在一系列的基函数上，而是直接对函数空间加上Bayes先验，即通用的平滑性约束;因此该模型中没有大量的参数，取而代之的是GP先验中协方差函数(核函数)的超参数，这就将模型转化为非参数Bayes模型，从而解决了过拟合问题.

高光谱遥感成像(hyperspectral remote sensing)［17］是光谱分辨率在10～20 nm 的光谱遥感，可获得几百个地物波段的光谱信息，具有波段数众多、非线性、空间相关性和谱间相关性共存、难以获得样本标记等特点.遥感图像分类是遥感地理信息系统中的关键技术之一，快速、高精度的遥感图像自动分类算法是实现环境的动态监测、评价、预报的关键.如何把新的模式分析和图像处理理论运用于高光谱影像分类是当前的研究热点之一.

本文首先介绍GP的基本理论及其发展;然后分析了高光谱图像的特点及其当前常用的分类方法;在此基础上结合笔者的研究成果，重点讨论用于高光谱图像分类的GP算法及其各种改进;最后给出了今后可能的一些关键研究问题.

1 GP基本理论

GP是在Bayes框架中对函数f(x)进行推理，故对函数f(x)在函数空间概率分布的可能形式给出先验.在GP模型中，假设这样的先验分布符合GP:

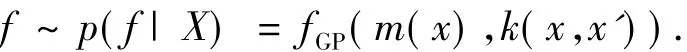
式中:fGP由均值函数m(x)和协方差函数k(x，x')完全确定，即m(x)=E［f(x)］，k(x，x')=cov［f(x)，f(x')］.而且，对于由任何x所对应的函数值的集合中的任意子集，也假设服从多元高斯分布，其均值和方差可以直接由均值函数m(x)和协方差函数k(x，x')分别计算出来.

GP的先验意味着在观察训练样本以前，就相信函数f(x)的可能形式是从先验p(f)中随机采样而实现的，根据训练数据D，函数f的先验可以更新成后验分布p(f|D).

1.1 高斯过程回归(Gaussian process regression，GPR)

回归问题的定义为:给定训练数据D={(xi，yi)，i=1，2，…，n}，对于新输入x*，预测其输出y*.

GP是把多元高斯分布推广到无限多个随机变量的形式.假设数据服从GP先验，则数据集合中的任意有限长的子集都服从联合多元高斯分布，其核函数为K，则

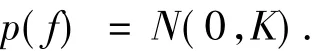
目标是求得p(y)的边缘分布，可用如下积分:

式中协方差矩阵C中的元素如下:

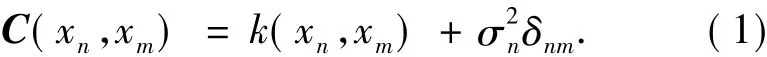
要预测y*，需要求出分布p(y*|yN).这里yN表示N个数据向量(y1，y2，…，yN)T，同理 yN+1表示(y1，y2，…，yN，y*)T.根据 GP 假设，联合分布为

式中:CN是N×N的协方差矩阵，其元素由式(1)而得;向量K有N个元素k(xn，xN+1)组成，其中n=1，2，…，N;C 的元素c=k(xN+1，xN+1)+

根据高斯分布性质，p(y*|yN)也是高斯分布，其均值和方差分别为:

根据Bayes决策论，损失函数最小化值为预测分布的中值，这里预测分布p(y*|yN)为高斯分布，故可用其均值来作为y*的预测值.

1.2 高斯过程分类(Gaussian process classification，GPC)

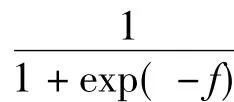
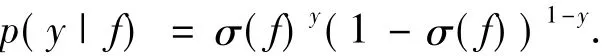
将f(x1)，f(x2)，…，f(xN)，f(x*)记作向量 fN+1.对于fN+1，GP的形式为

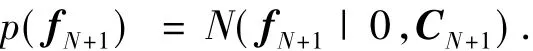
式中:CN+1定义和式(2)中一致.

对于分类问题，其实就是求p(y*=1|y)的分布，该分布形式为

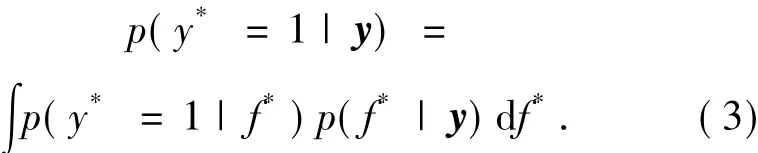
由于式(3)中被积分函数中2个分布函数不是高斯分布的乘积形式，求不出解析解，因此通常可以用 Laplace 法［14］、变分法［15］、MCMC［16］、EP［18］和其他近似算法［19－20］求解.

1.3 GP的核函数

在机器学习领域中，协方差函数通常称为核函数［21］.核函数具有超参数 θ，表示为k(x，x';θ).一般地，假设均值函数m(x)=0，则选择核函数类型并确定超参数就可以将GP确定下来.

GP是基于核函数的方法.核函数是GP预测和分类的关键因素，集成了待学习函数的假设.函数要成为有效核函数的充分必要条件是，矩阵元素为k(xm，xn)构成的Gram矩阵K必须是半正定矩阵［21］.GP核函数可以是多种函数形式，如高斯核函数、神经网络核函数、多项式核函数等，也可以通过2个核函数的相加、相乘、卷积等运算来构造新的核函数.

1.4 GP超参数的训练

超参数求解方法的思想来自于求出使得似然函数p(y|θ)取最大值的GP超参数θ.最简单的方法是通过求最大对数似然函数来求出θ的点估计，该求解过程可以通过类似于共轭梯度法或其他基于梯度的优化算法来完成［22－23］.GP 的对数似然函数形式为

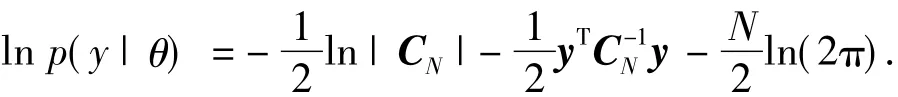
将对数似然函数对于超参数θ求梯度，得到

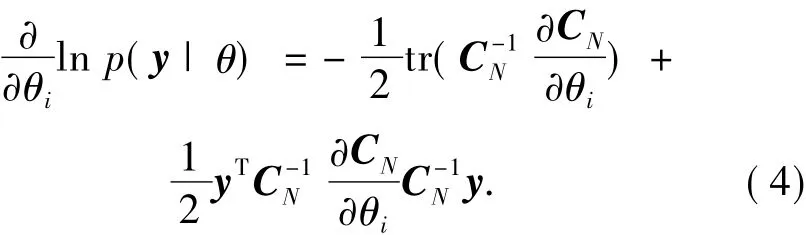
这样可以根据训练样本集D求得式(4)中的最大值而得到最优的超参数^θ.

1.5 带约束的GP

目前，有一些学者对于带约束的GP进行了一些研究.通常，约束通过判别高斯过程隐变量模型(discriminative Gaussian processeslatentvariable model，D－GPLVM)加在低维数据流形上.

R.Urtasun［24］指出只要数据存在低维流形，DGPLVM可以在训练样本很少而数据维数很高的情况下分类，并得到较好的分类精度.D－GPLVM方法通过在高斯过程隐变量模型(GPLVM)的数据隐空间中加上判别式先验，就可以通过判别的方式来学习GP分类器的协方差矩阵，从而达到提高分类精度的目的.该判别式先验标准可以是广义判别分析(generalized discriminative analysis，GDA)［25］，也可以是局部费舍尔判别分析(local Fisher discriminative analysis，Local FDA)［26］或者其他判别函数.Grochow在文献［27］中通过尺度化高斯过程隐变量模型(scaled GPLVM)，从低维空间上给人体姿态进行约束，对于人体的姿态进行插值，从而对人的动作进行预测.

另外，可以通过在GP中加载稀疏性约束来获得大数据集上GP的近似解.L.Csató在文献［28］中提出利用约束GP来求得真实后验稀疏近似解.该方法通过增加参数的数量使得GP可以突破计算限制用于任意大的数据集，该近似解法基于最小化原始GP和带约束GP之间的KL距离，带约束GP的约束指的是，整个训练样本中只有很少量的子集用来表示GP，该约束导致稀疏性.

1.6 基于半监督学习的GP

GP可与半监督学习相结合，这时半监督可以看成是加在GP上的一种特殊的平滑性约束.

半监督学习可以利用少数带标记样本加上大量无标记样本，从而提高分类和预测精度.半监督学习方法最初基于几何直觉，对于许多现实问题，无标记样本经常可以识别出整个数据的结构，如数据聚类或低维流型，这些知识可以帮助进行推理.例如，人们常期望在一个聚类中的数据点间或者在一个流形中相近的数据点间的类别有很强的相关性，这就是半监督学习中的聚类假设和流形假设.

最近，有一些学者提出多个基于图集成无标记训练样本的半监督GP算法.文献［29］中提出基于图先验知识的直推式高斯过程(transductive GP)，其核心概率模型只是定义在带标记样本和无标记样本的有限训练集合上，但需要额外的过程将模型扩展到未知的测试样本中.

文献［30］中提出的半监督高斯过程方法中，将无标记数据的空间属性和基于图的半监督核函数结合起来，建立了在整个空间上的GP模型，提供了天然的样本之外数据的预测能力.正则化算子加在图顶点上的平滑性被转换成为定义在整体数据空间上的再生核希尔伯特空间(reproducing kernel Hilbert spaces，RKHS).通过该RKHS核函数，标准的监督核方法可以用来进行半监督推理.

Zhu在文献［29］中指出高斯随机场(Gaussian random field，GRF)和半监督学习中的谐能量最小化函数框架可以看成是协方差矩阵源自图Laplace的GP，从半监督学习的角度指出了GRF与GP在概率框架中的联系.

综上，GP作为一种核方法，可用于分类和回归，其超参数可由训练得到，GP模型加上约束后可以有较多变形算法，这为GP在实际问题中的应用提供了较强的理论基础.

2 高光谱图像

2.1 高光谱遥感图像的特点

2.1.1 高维非线性

高光谱遥感图像由卫星或飞机上携带传感器记录而成.图像数据包含像素的2种误差:辐射误差和几何误差［17］.数据记录仪器、太阳辐射对波长的依赖和大气影响都可能产生辐射误差.图像几何误差产生是多方面的，如平台、扫描仪与地球的相对运动可能导致图像的扭曲，传感器本身非理想特性、地球曲率以及遥感平台在位置和姿态方面无法控制的变化都可能导致不同程度的几何误差.

辐射误差可以通过某些计算方法进行补偿.而几何误差由于其产生因素较复杂，很难完全去除其影响，这就使得高光谱图像不同程度上具有非线性的特性，造成图像很难进行线性拟合，也难以用线性分类器对高光谱图像进行正确分类.

2.1.2 空间相关性和谱间相关性共存

空间相关性是指每个谱段内某一像素与其相邻像素之间的相似性.谱间相关性是指每个谱段光谱图像的同一空间位置像素具有相似性.高光谱图像中，相邻像素之间在空间上总存在一定联系.首先，传感器在对该像素成像时，同时吸收了周围像素的一部分能量;其次，某一地物类别在地面所占的实际面积与一个像素的实际面积相比也大得多.例如，一个农业区域，已知某一像素代表小麦，那么它周围的像素是小麦的概率比不是小麦的概率要大很多.相邻像素点之间的空间相关性的强弱主要取决于传感器的空间分辨率和地表自然、人文区域的规模大小［17］.

高光谱图像的谱间相似性的产生原因有2点:一是光谱图像的每个波段图像的像素值，是相同区域地物在各个波段的反射值，它们是具有相关性的，其相关性的强弱在很大程度上取决于光谱分辨率;二是由于不同波段的图像所涉及的地面目标相同，它们具有相同的空间拓扑结构.

2.1.3 训练样本标记难以获得

目前用于高光谱遥感图像的有监督分类算法，由于波段数量巨大，需要大量正确的训练样本.然而，获得样本标记不仅费时费力，而且在许多情况下，很难对样本进行标记，例如森林大火、山体滑坡、洪水和地震，获得标记的训练样本是不可能的.

另一方面，根据Hughes的研究结果［31］，随着特征空间维数的增加，类别可分性提高，但由于遥感中常用的监督分类方法首先要顾及样本的分布函数或者分布函数中的一些参数，随着空间维数的增加，待估计参数的急剧增加，在训练样本数量一定的条件下，导致分类精度在特征空间的维数增加到一定数量后，反而会随着维数的增加而下降.为了保持分类精度，通常有2种措施，一是在分类前对原始光谱空间进行降维预处理，得到一个保持了原始空间全局和局部特征结构的低维子空间，然后在低维子空间中进行分类判别［32］;二是尽可能增加训练样本的数量，由于带标记的训练样本难以获得，因此这点通常难以做到.

2.2 高光谱遥感图像分类

高光谱遥感图像分类方法以统计模式识别方法占主流，包括传统遥感图像分类方法、基于核函数分类方法和其他分类方法.

1)传统遥感图像分类主要分为有监督分类和非监督分类.监督分类包括:最大似然分类法、Bayes分类法、最近邻分类法、KNN分类法、费舍尔判别分类、多尺度自回归［33］等.这些方法在对高光谱图像分类时往往无法获得足够的训练样本，容易引起Hughes现象.非监督方法主要是聚类法，按照图像的光谱特征的分布规律，以某种相似性测度自动聚集成类，其分类结果只是对不同类别进行了区分，主要包括K均值法、ISODATA法、分级聚类等.

2)核函数方法通过非线性映射，将输入空间的样本映射到高维特征空间中，在高维空间中构造分类判决面进行分类.核函数方法包括:SVM、GP、核主成分分析、核函数费舍尔判别法(kernel Fisher discriminant，KFD)、核投影寻踪法等，这些方法都在高光谱图像处理中得到了应用.

3)其他分类方法主要包括神经网络分类法［34］、决策树分类法等.

在高光谱遥感图像分类上，核函数方法占有一定优势，原因在于:一方面，高光谱图像的波段数一般较大，线性分类器通常很难将其有效分开，核函数方法可以将输入空间映射到高维空间，在高维空间更易于找到有效的线性分类器，通常可以取得较好的分类效果;另一方面，核函数方法为非参数方法，只需要对少数几个超参数进行学习，速度较快，也比较简单，而其他参数方法通常要学习很多参数，学习过程较长，也比较复杂.

SVM因具备能有效处理较多输入波段，鲁棒地处理带噪声样本，产生稀疏解等优点，近几年被成功应用于高光谱遥感图像分类［35－36］.但 SVM 本身也存在着一些问题，如:特定问题中核函数的选取、核函数的参数选择、如何选取合适的惩罚项来防止过拟合、SVM的估计输出不具有概率意义.

另外高光谱图像的空间相关性可以为分类提供很多有用的信息，正确的使用上下文空间信息可以纠正由于噪声影响或者分类器缺陷引起的孤立像素错分，从而提高分类精度.关于遥感图像的上下文分类，很多学者做了有用的探索［37－38］，典型的方法有Kriging［39］、MRF［40］、条件随机场(conditional random field，CRF)方法［41］等.CRF是 Lafftery于2001年新提出的方法［42］，Kumar［43］于 2003 年将其有效地运用于图像的人工建筑物检测，Zhong［41］将其用于高光谱遥感图像的目标检测.

3 基于GP的高光谱图像分类

GP和SVM一样，也是基于核函数的方法，具有核函数方法分类的优势.与SVM不同的是，GP具有完全的Bayes公式化表示，所以能够明确地进行概率建模，使结果更易于解释.更重要的是，GP的Bayes学习提供了一个范式，根据训练样本，从先验分布到后验分布的转换，可以对核函数的超参数进行推理，而SVM对超参数的选择却通常只能采用经验法或者交叉验证方法.

高光谱图像具有高维非线性、空间相关性和谱间相关性共存以及训练样本难以获得的特点;故使用GPC时，应充分针对上述特点，将GP进行改进，使其更适用于高光谱图像分类.

GP的核函数可以有多种不同的形式，如线性核函数、多项式核函数、高斯核函数、指数核函数等.高光谱图像中多个谱段的像元之间近似服从高斯分布，故采用高斯形式核函数的GP来对高光谱图像进行分类较为合理.

标准GPC只利用高光谱图像的谱间相关性，并没有利用空间相关性.CRF利用高光谱图像的空间相关性，可以根据邻域像元将错分类孤立像元类别纠正.构造CRF和GP相结合的GPCRF分类器进行高光谱图像分类，能够进一步提高图像分类精度.

由于高光谱图像的训练样本难以获得，在少量训练样本下进行监督GPC，将给参数估计带来较大误差，导致分类精度严重下降.考虑在遥感图像上可以获得大量的无标记的训练样本，在GP中引入半监督学习思想，充分利用大量无标记样本所蕴含的信息辅助分类，构造半监督高斯过程(semi－supervised Gaussian process，SSGP)分类器，能够有效克服高光谱图像训练样本少的问题.

3.1 实验数据集

下面将详细介绍几种笔者提出的改进的GPC算法，并给出相应的高光谱图像分类实验结果.首先介绍一下实验采用的高光谱遥感数据.

1)高光谱遥感实验数据一是AVIRIS传感器于1992年拍摄的220个波段印第安纳州西北区域高光谱遥感图像，图像大小为145×145，取其中非耕犁玉米地、最小耕犁玉米地、牧草、禾木、干草、非耕犁大豆地、最小耕犁大豆地、完全耕犁大豆地和林地9个不同类别做实验，见图1.

图1 印第安纳AVIRIS第25波段Fig.1 Hyperspectral image of AVIRIS in Indiana 92，Band 25

2)高光谱遥感实验数据二是HYDICE传感器拍摄的华盛顿特区的某区域，该子图有500×307个像元，210个波段，由屋顶、道路、水、草、树、人造建筑和阴影7个类组成，见图2.

图2 华盛顿特区HYDICE第80波段Fig.2 Hyperspectral image of HYDICE in Washington D.C.，Band 80

在基于GP的高光谱遥感分类中，图像数据表示成D={xi，yi}，xi为某个特定像元，yi为像元xi的类别标签，矢量x表示高光谱像元的波段矢量，若遥感数据光谱波段为n维，则每个xi都是n维数据.

3.2 基于非线性核函数GP的高光谱图像分类

高光谱图像具有高维非线性的特性，而GP是一种非线性Bayes核函数方法，通过采用非线性核函数，比如高斯核函数GP可以较好地解决高光谱遥感图像的非线性问题.这里用线性核函数和高斯核函数分别做实验进行比较.

线性核函数形式为

高斯核函数形式为

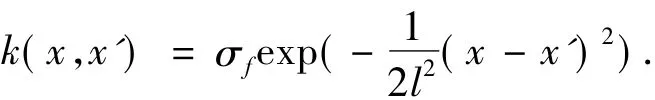
式中:σf和l均为超参数.用线性核函数高斯过程分类方法和高斯核函数高斯过程分类方法其训练时间都为O(n3)，测试时间都为O(mn2)，其中n为训练样本的个数，m为测试样本的个数.这2种分类方法的实验结果如图3.根据实验结果可以看出，2幅不同的高光谱遥感图像，高斯核函数GPC精度均明显优于线性核函数GP.因此可以得出结论，高斯核函数的GP更适合于高维非线性高光谱图像分类.

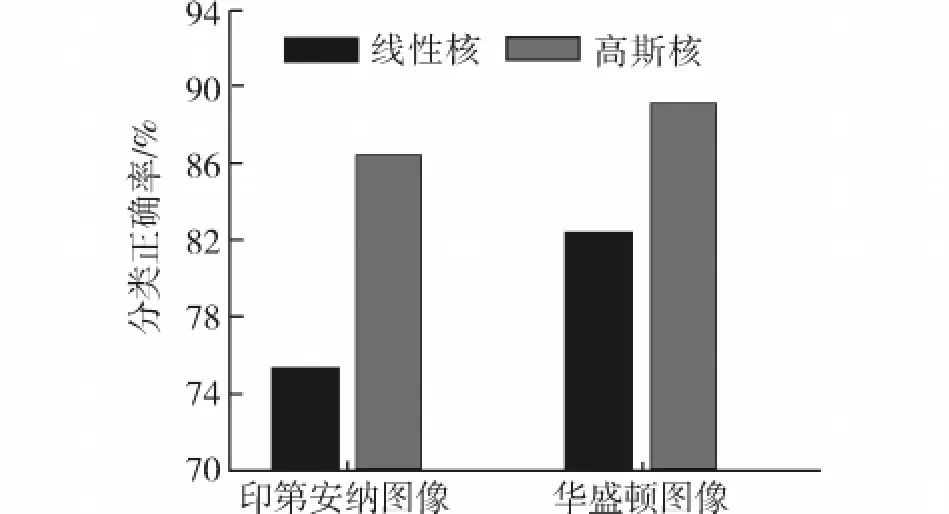
图3 2种不同核函数GP高光谱图像分类对比Fig.3 Comparing results of linear kernel GP and SE kernel GP classification

3.3 基于GPCRF的高光谱图像分类

结合高光谱图像特点，可以在GPC加上空间相关性约束，把GP分类框架和CRF框架结合起来，先通过GP框架求出每个像元的隐函数值，再将隐函数值代入到CRF框架中，通过求最大后验法则求出整幅图像的类别.

3.3.1 GPCRF模型

用于图像分析时，CRF可以写成如下形式:

式中:x是观察值;y是像素点的类别标签;Ai称为联合势能，Iij称为相互作用势能，Ai仅与单个变量xi有关，Iij则与一对相邻变量有关;Ni为变量i的邻域，但它们都与观察量y而不仅仅与yi有关系，这里可看出CRF能利用丰富的特征建模.

GP和CRF组合构成的GPCRF分类器，可以利用高光谱图像中的光谱和空间的相互作用，通过用GP中的隐函数f来代替式(4)中的联合势能，可得式(5):

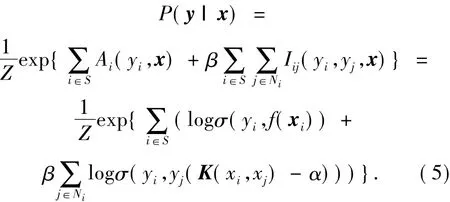
式中:Z称为配分函数，实际为所有y的取值情况之和.式(5)表示在已知整幅高光谱图像像元的光谱信息条件下整幅图像类别的条件概率.根据最大后验法则，整幅图像类别y最佳取值为使得条件概率最大时y的取值，故求解时应通过估计算法求出后验概率最大值时的y值，就可对整幅图像所有像元都加上该类别标签.

GPCRF分类方法的训练时间为O(MNn3)，测试时间为O(MNn2)，其中n为训练样本的个数，m为测试样本的个数，M为整幅图像的像素点个数，N为邻域内像素点个数.

3.3.2 实验结果及分析

在印第安纳遥感图像和华盛顿特区遥感图像上均进行了GP分类实验和GPCRF分类实验.图像数据一中训练样本与测试样本数目比例近似于1:1，图像数据二中训练样本与测试样本比例为1:4，其中的GP模型采用Laplace法近似，GPCRF采用ICM(iterated conditional modes)法来计算最大后验.

图4 印第安纳图像不同邻域阶数GP与GPCRF分类比较Fig.4 Comparing results of Indiana classification accuracy GP and GPCRF in different order numbers

图5 华盛顿特区图像不同邻域阶数GP与GPCRF分类比较Fig.5 Comparing results of Washington D.C.classification accuracy GP and GPCRF in different order numbers

图4和图5表明了2个数据集在不同的邻域阶数下GPCRF方法的平均分类正确率，同时为了进行比较，也给出了GP方法的分类结果.从实验结果可以看出，分类正确率基本上随着邻域阶数的提高而提高.另外，GPCRF方法的计算时间并没有随着邻域阶数的提高而增加太多.根据实验结果，可以得出2点结论:1)被分错的数据零散地分布在每个类中，并且随着邻域的阶数提高，GPCRF方法中的空间相关性越来越重要;2)当训练样本的比例相对高的时候，GPCRF可以对高光谱图像分类得到较好的结果.

3.4 基于半监督GP的高光谱图像分类

高光谱遥感图像分类之前，为了避免Hughes现象，应先对图像进行特征选择.针对高光谱图像特征选择，目前有很多相关研究工作［44－46］.然而即使进行了特征选择，由于高光谱遥感图像难以获得大量训练样本标记，分类依然是一个小样本的问题，这就会导致参数估计带有大的方差，以致于分类错误率较高，而高光谱遥感图像上大量的无标记的样本可用来进行辅助分类［47］.

3.4.1 SSGP数学模型

标准GP由其核函数惟一决定.SSGP通过在数据低维流形上加平滑性约束来构造半监督核函数，通过半监督核函数来对测试样本进行分类.SSGP中半监督核函数构造公式如式(6):

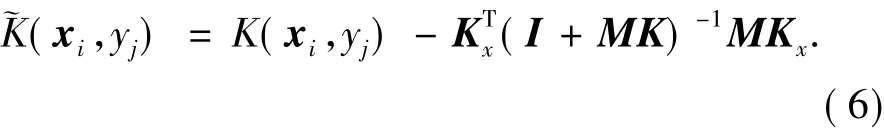
从式(6)可以看出，构造半监督核函数的关键是如何选择M矩阵，以反映我们对于数据几何特性的直觉，该直觉可以来自于无标记数据的边缘分布.在文献［48］中，采用图拉普拉斯(graph－Laplacian)来描述数据的结构，实现了边缘分布几何结构平滑的假设.

SSGP分类方法的训练时间为O(l2n3)，测试时间为O(lmn2)，其中n为训练样本的个数，m为测试样本的个数，l为未标记训练样本的个数.

3.4.2 实验结果及分析

在印第安纳遥感图像和华盛顿特区遥感图像上均进行了标准GP的分类实验和SSGP的分类实验.在实验数据一中随机选取853个像元作为带标记训练样本，在实验数据二中随机选取1 400个像元作为带标记训练样本.然后分别在2幅图像中任意取若干比例的像元作为无标记训练样本，剩下的像元作为测试样本.通过M=L形式构造M矩阵.实验结果如图6和图7所示.

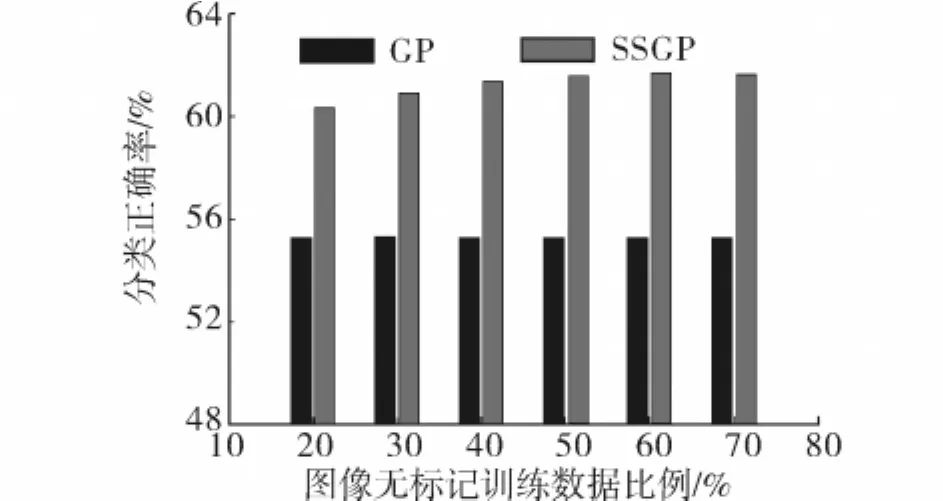
图6 印第安纳图像GP与SSGP分类比较Fig.6 Comparing results of Indiana classification accuracy GP and SSGP

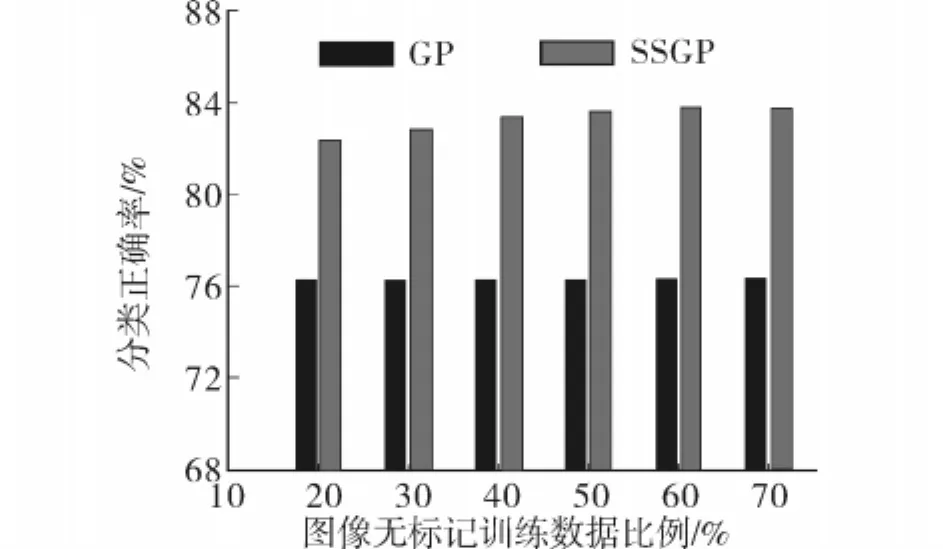
图7 华盛顿特区图像GP与SSGP分类比较Fig.7 Comparing results of Washington D.C.classification accuracy GP and SSGP

从这2个数据集的实验结果中，不难发现，SSGP方法与有监督GP相比，在少量训练样本的情况下，分类精度有了较大的提高.因此，空间约束的半监督GP通过引入未标记数据信息，使得分类算法性能得到提升，充分显示了SSGP算法的有效性.

另外，可以看出，当无标记的训练样本数量增加到某个程度后，再提高无标记训练样本数量，对于分类精度的提升几乎没有帮助.这体现了空间流形假设仅在一定邻域范围内有效，超出该邻域范围，基于空间流形假设的半监督学习将不再有效.

4结论

本文总结了基于GP的高光谱图像分类技术近年来的研究进展，重点讨论了高光谱图像本身的特点，以及针对以上特点，将GP适当变形，进一步提高分类精度的一些算法.基于GP的高光谱遥感图像分类，仍需要进一步的发展和完善，未来的研究方向如下:

1)高光谱数据在空间上和波段上存在着大量冗余.如何针对这一特点来进行GP训练样本的选择，有效减少训练样本数目而又不影响GP预测和分类精度，这是一个重要的研究目标.

2)高光谱图像波段数较多，地物的光谱曲线连续，可利用地物物理光学性质的光谱曲线进行地物识别.如何将GP分类方法与基于光谱曲线的匹配方法结合起来，进一步提高分类精度，有很大的实用价值.

3)基于GP的高光谱图像分类往往先做特征选择，再进行分类，这2个步骤是割裂的，相互之间几乎没有联系.如何将特征选择和GP分类有机结合起来，使得特征选择的结果更适用于分类，也是值得研究的一个问题.

［1］WIENER N.Extrapolation，interpolation，and smoothing of stationary time series，with engineering applications［M］.Cambridge，USA:MIT Press，1949:102－106.

［2］MATHERON G.The intrinsic random functions and their applications［J］.Advances in Applied Probability，1973，5(3):439－468.

［3］JOURNEL A G，HUIJBREGTS C J.Mining geostatistics［M］.New York，USA:Springer－Verlag，1978:304－310.

［4］THOMPSON P D.Optimum smoothing of two－dimensional fields［J］.Tellus，1956，8(3):384－393.

［5］DALEY R.Atmospheric data analysis［M］.Cambridge，UK:Cambridge University Press，1993:99－107.

［6］WHITTLE P.Prediction and regulation by linear leastsquare methods［M］.London，UK:English Universities Press，1984:58－69.

［7］RIPLEY B D.Spatial statistics［M］.Hoboken，USA:Wiley－IEEE，2004:44－50.

［8］CRESSIE N.Statistics for spatial data［J］.Terra Nova，1992，4(5):613－617.

［9］O’HAGAN A，KINGMAN J F C.Curve fitting and optimal design for prediction［J］.Journal of the Royal Statistical Society:Series B(Methodological)，1978，40(1):1－42.

［10］SACKS J，WELCH W J，MITCHELL T J，et al.Design and analysis of computer experiments［J］.Statistical Science，1989，4(4):409－423.

［11］SANTNER T J，WILLIAMS B J，NOTZ W.The design and analysis of computer experiments［M］.New York，USA:Springer－Verlag，2003:61－65.

［12］WILLIAMS C K I，RASMUSSEN C E.Gaussian processes for regression［M］.Cambridge，USA:MIT Press，1996:25－37.

［13］RASMUSSEN C E，WILLIAMS C K.Gaussian processes for machine learning［M］.Cambridge，USA:MIT Press，2006:15－30.

［14］WILLIAMS C K I，BARBER D.Bayesian classification with Gaussian processes［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1998，20(12):1342－1351.

［15］GIBBS M N，MACKAY D J C.Variational Gaussian process classifiers［J］.IEEE Transactions on Neural Networks，2000，11(6):1458－1464.

［16］NEAL R.Regression and classification using Gaussian process priors［J］.Bayesian Statistics，1998，6(10):475－501.

［17］CHANG C I.Hyperspectral imaging:techniques for spectral detection and classification［M］.New York，USA:Kluwer Academic Plenum Publishers，2003:8－16.

［18］MINKA T P.A family of algorithms for approximate Bayesian inference［D］.Cambridge:Massachusetts Institute of Technology，2001:36－48.

［19］GIBBS M N，MACKAY D J C.Variational Gaussian process classifiers［J］.IEEE Transactions on Neural Networks，2002，11(6):1458－1464.

［20］SEEGER M.Bayesian model selection for support vector machines，Gaussian processes and other kernel classifiers［M］//SOLLA S A，LEEN T K，MULLER K L.Advances in Neural Information Processing Systems.Cambridge，USA:the MIT Press，2000:603－609.

［21］SHAWE－TAYLOR J，CRISTIANINI N.Kernel methods for pattern analysis［M］.Cambridge，UK:Cambridge University Press，2004:48－57.

［22］FLETCHER R.Practical methods of optimization:constrained optimization［M］.Hoboken，USA:John Wiley＆Sons Inc，1984:87－94.

［23］NOCEDAL J，WRIGHT S J.Numerical optimization［M］.New York，USA:Springer－Verlag，1999:53－64.

［24］URTASUN R，DARRELL T.Discriminative Gaussian process latent variable model for classification［C］//International Conference on Machine Learning.Corvallis，USA，2007:934－937.

［25］BAUDAT G，ANOUAR F.Generalized discriminant analysis using a kernel approach［J］.Neural Computation，2000，12(10):2385－2404.

［26］SUGIYAMA M.Local Fisher discriminant analysis for supervised dimensionality reduction［C］//International Conference on Machine Learning.Pittsburgh，USA，2006:905－912.

［27］GROCHOW K，MARTIN S L，HERTZMANN A，et al.Style－based inverse kinematics［J］.ACM Transactions on Graphics，2004，23(3):522－531.

［28］CSAT L.Gaussian processes:iterative sparse approximation［D］.Birmingham，UK:Aston University，2005:26－34.

［29］ZHU Xiaojin，GHAHRAMANI Z，LAFFERTY J.Semi－supervised learning using Gaussian fields and harmonic functions［C］//Proceedings of the 20th International Confer－ence on Machine Learning.Washington，DC， USA，2003:912－914.

［30］SINDHWANI V，CHU W，KEERTHI S S.Semi－supervised Gaussian process classifiers［C］//International Joint Conference on Artificial Intelligence.Hyderabad，India，2007:1059－1064.

［31］HUGHES G.On the mean accuracy of statistical pattern recognizers［J］.IEEE Transactions on Information Theory，1968，14(1):55－63.

［32］QIAN Y，YAO F，JIA S.Band selection for hyperspectral imagery using affinity propagation［J］.IET Computer Vision，2010，3(4):213－222.

［33］贺霖，潘泉，邸韦华，等.高光谱图像高维多尺度自回归有监督检测［J］. 自动化学报，2009，35(5):509－518.

HE Lin，PAN Quan，DI Weihua，et al.Supervised detection for hyperspectral imagery based on high dimensional multiscale autoregression［J］.Acta Automatica Sinica，2009，35(5):509－518.

［34］熊桢，童庆禧.用于高光谱遥感图象分类的一种高阶神经网络算法［J］.中国图象图形学报，2000，5(3):196－201.

XIONG Zhen，TONG Qingxi.High－rank artificial neural network algorithm for classification of hyperspectral image data［J］.Journal of Image and Graphics，2000，5(3):196－201.

［35］MELGANI F，BRUZZONE L.Classification of hyperspectral remote sensing images with support vector machines［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42(8):1778－1790.

［36］刘春红.超光谱遥感图像降维及分类方法研究［D］.哈尔滨:哈尔滨工程大学，2005:86－94.

LIU Chunhong.Research on dimensional reduction and classification of hyperspectral remote sensing image［D］.Harbin:Harbin Engineering University，2005:86－94.

［37］KITTLER J，PAIRMAN D.Contextual pattern recognition applied to cloud detection and identification［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，23(6):855－863.

［38］姚伏天，钱沄涛.用于高光谱遥感图像分类的空间约束高斯过程方法［J］.南京大学学报:自然科学版，2009，45(5):665－670.

YAO Futian，QIAN Yuntao.A spatial Gaussian process method for hyperspectral remote sensing imagery classification［J］.Journal of Nanjing University:Natural Sciences，2009，45(5):665－670.

［39］ROSSI R E，DUNGAN J L，BECK L R.Kriging in the shadows:geostatistical interpolation for remote sensing［J］.Remote Sensing of Environment，1994，49(1):32－40.

［40］DENG H，CLAUSI D A.Advanced Gaussian MRF rotation－invariant texture features for classification of remote sensing imagery［C］//Computer Society Conference on Computer Vision and Pattern Recognition.Madison，USA，2003:685－689.

［41］ZHONG Ping，WANG Runsheng.A multiple conditional random fields ensemble model for urban area detection in remote sensing optical images［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45(12):3978－3988.

［42］LAFFERTY J，MCCALLUM A，PEREIRA F.Conditional random fields:probabilistic models for segmenting and labeling sequence data［C］//Proceedings of the Eighteenth International Conference on Machine Learning.Williamstown，USA，2001:282－289.

［43］KUMAR S，HEBERT M.Discriminative random fields［J］.International Journal of Computer Vision，2006，68(2):179－201.

［44］LI Jiming，HU Zhenfang，QIAN Yuntao.Hyperspectral data classification using margin infused relaxed algorithm［C］//International Conference on Image Processing.Hong Kong，China，2009:1669－1672.

［45］LI Jiming，QIAN Yuntao.Regularized multinomial regression method for hyperspectral data classification via pathwise coordinate optimization［C］//Digital Image Computing:Techniques and Applications.Melbourne，Australia，2009:540－545.

［46］YAO Futian，Qian Yuntao.Band selection based Gaussian processes for hyperspectral remote sensing images classification［C］//International Conference on Image Processing.Hong Kong，China，2009:2845－2848.

［47］VATSAVAI R R，SHEKHAR S，BURK T E.A semi－supervised learning method for remote sensing data mining［C］//International Conference on Tools with Artificial Intelligence.Hong Kong，China，2005:205－211.

［48］BELKIN M，NIYOGI P，SINDHWANI V.Manifold regularization:a geometric framework for learning from labeled and unlabeled examples［J］.The Journal of Machine Learning Research，2006，7:2399－2434.

姚伏天，男，1976年生，博士研究生，主要研究方向为模式识别、机器学习、高光谱成像信息处理，发表学术论文20余篇.

钱沄涛，男，1968年生，教授，博士生导师，中国计算机学会人工智能与模式识别专业委员会委员、模糊逻辑与多值逻辑专业委员会委员.主要研究方向为模式识别、机器学习、信号处理，承担多项国家自然科学基金项目、国际合作基金项目和省部级重点科技项目，发表学术论文70余篇.

Gaussian process and its applications in hyperspectral image classification

YAO Futian1，2，QIAN Yuntao1，2
(1.College of Computer Science，Zhejiang University，Hangzhou 310027，China;2.Institute of Artificial Intelligence，Zhejiang University，Hangzhou 310027，China)

Hyperspectral image classification is one of the hotspots in the field of remote sensing applications.The classification performance is affected by the inherit characteristics of hyperspectral imaging.Gaussian process(GP)is a recently developed machine learning method which enables explicitly probabilistic modeling and makes results easily interpretable.Furthermore，hyper－parameters of GP can be learned from training data，which overcomes the difficulties of fixing model parameters in most classifiers.This paper introduced the basic concept of GP and some GP－based classification methods.After analyzing the characteristics of hyperspectral imaging and the existing classification methods for hyperspectral images，GP based classification for hyperspectral images was discussed，and some new GP－based classification methods such as GP with spatial constraints and semisupervised GP methods were proposed.Finally，several future research trends of GP and hyperspectral image classification were given.

Gaussian process;hyperspectral imaging;machine learning;image classification

TP181

A

1673－4785(2011)05－0396－09

10.3969/j.issn.1673－4785.2011.05.003

2010－10－19.

国家自然科学基金资助项目(60872071).

钱沄涛.E－mail:ytqian@zju.edu.cn.