主路优先无信号交叉口次要道路通行能力分析＊

丁 川 谢秉磊 张昕明

（哈尔滨工业大学深圳研究生院 深圳 518055）

无信号交叉口是最普遍的交叉口类型，它往往是路网中交通流的瓶颈，无信号交叉口的通行能力严重影响着整个路网的通行能力，在城市道路网中具有非常重要的作用.当一个无信号交叉口运行状况不良时，可能会导致所连接路段的拥挤，甚至波及整个路网和运输系统的运行.因此，对于无信号交叉口通行能力的研究具有重要意义.

主路优先无信号交叉口次要道路通行能力的计算方法包括理论法与经验法.理论法是基于条件假设，推导出计算通行能力的公式模型，进而精确定量分析.经验法则是根据交通调查数据，进而统计分析所得，结果精度不高.无信号交叉口次要道路通行能力的研究一直是热点，很多学者对此作了研究，也取得了丰硕的研究成果.D.P.Sullivan［1］证明了 M3分布能更好地拟合城市道路上交通流车头时距的实际情况，R.J.T.Rout beck给出了当主路车流的车头时距服从交通流流量为q（pcu／h）的M3分布，次要道路上的车辆为理想的单一车型时次要道路的通行能力［2］.目前主路优先无信号交叉口次要道路通行能力的计算研究主要采用可接受间隙理论和概率论方法，一些学者也用此方法建立了多转向多车型的混合车流情况下次要道路通行能力模型［3－10］.本文对理想条件下次要道路通行能力模型进行推导分析，运用随机过程的马尔可夫理论建立考虑多转向多车型的混合车流情况下次要道路的通行能力模型.

1 无信号交叉口次要道路通行能力理想计算模型

1.1 无信号交叉口的特征

平面交叉口的通行能力受到平面交叉口的形状、渠化、进口道的车道宽度等几何构造的影响，同时也受到交通组成、交通流速度等因素的影响，因此有必要分析无信号交叉口的特征.

几何特征 交叉形式一般为十字型，主要道路较次要道路宽，各方向进口道的坡度为零，而且行车视距良好.

车速特征 车辆运行速度不高，主要道路的行车速度较次要道路快.

车辆组成 车辆构成比较复杂，交通流中小车型比例很大，可将通过交叉口车辆分为3类，见表1.

表1 车辆分类 m

1.2 理想模型的推导

1.2.1 可插车间隙理论 可插车间隙理论指的是，主要道路车流优先通过交叉口，不产生延误，次路车流必须在交叉口前等待，只有当主要道路车流出现足够大的间隔，次要道路车辆才能通过［11］.由此可知，在可插间隙理论中最重要的两个参数是临界间隙时间（次要道路车流中驾驶员所能够接受的最小间隙时间）和次要道路车流中的随车时距.

计算机软件的发展虽然时间较短，其作用却不容忽视，直接影响着计算机未来的发展和进一步应用，因此，对计算机软件开发技术的研究就显得尤为重要了。计算机软件的开发技术是一个不断演变和发展的过程，虽然在应用过程中取得了一定的成效，但是要不断适应人们的生活和经济的发展，这就需要相关软件开发技术人员能够顺应时代的发展和要求，从长远角度出发，实现不断创新计算机软件开发技术。

首先推导理想条件下，只有2股车流情况下的次要道路通行能力（见图1）.

1.2.2 条件假设 （1）主要道路的车辆到达服从泊松分布；（2）次要道路穿越主要道路所能接受的临界间隙 和通过间隙时次要道路上车流的车头时距tf均为常数；（3）每股车流有稳定的流量，波动不大.

1.2.3 模型推导 设主要道路上单向交通量为q（pcu／h），λ＝q／3 600（pcu／s）主要道路上车流的车头时距概率密度为f（t），当主路上车流的间隙为t时，次要道路上可以穿越的车辆数为g（t），则次要道路的通行能力为次要道路穿越主要道路情况分析见表2.

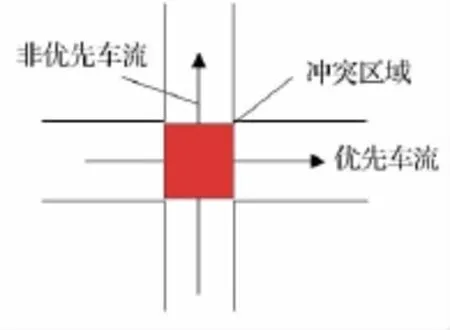
图1 理想条件下两股车流示意图

表2 次要道路穿越主要道路情况分析

所以，主要道路车头时距允许次要道路穿越的平均总车辆数为

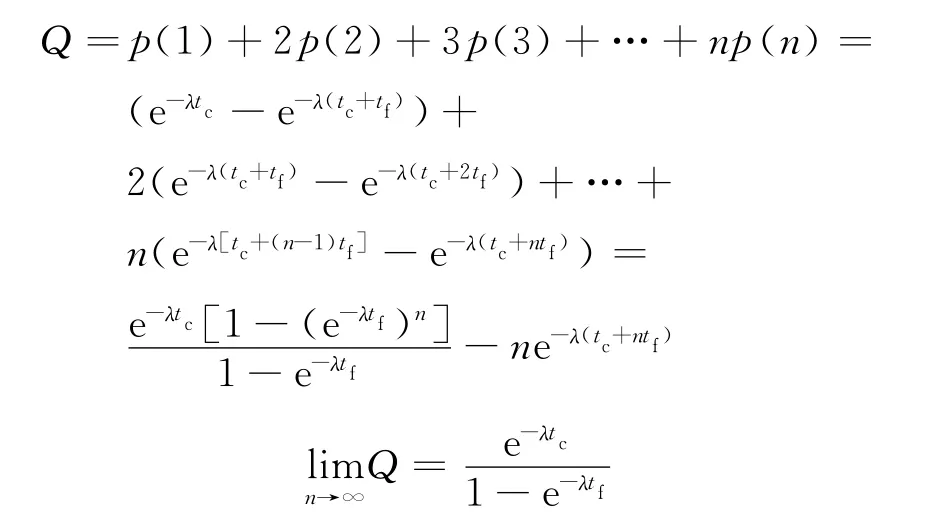
主要道路交通量为q，则每h主路上提供q个车头时距可穿越，所以次要道路的通行能力为

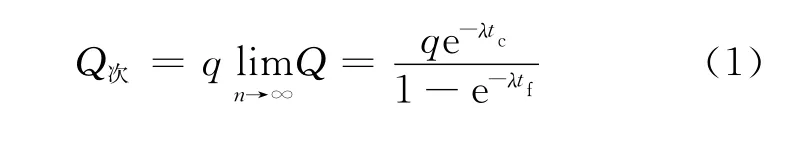
2 对理想模型的分析与修正

在模型的推导假设中，临界间隙时间tc和次要道路上的车头视距tf都取固定值，这与实际是不相符的.由于不同类型车辆所需的最小间隙时间是不同的，而且次要道路上的车辆类型存在差异，因此车头视距也不会是固定值.其次，两股车流的情况只是理想模型，在实际中也是几乎不存在的，实际中更为常见的是多车流多转向的形式.

基于理想模型中的不足，分析建立考虑车辆类型及其转向的主路优先无信号交叉口次要道路通行能力.根据主要道路和次要道路交叉口的实际情况，次要道路进口道最常见的形式是一条右转车道，一条直、左共用的车道，见图2.

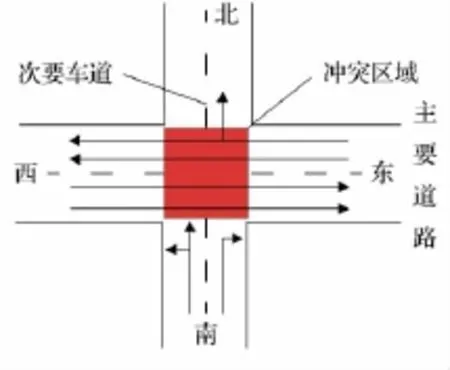
图2 常见十字型交叉口示意图

主要道路为双向4车道：西进口道为2条直行车道；东进口道有1条直行、右转合用车道，1条直行车道.次要道路为单向2车道：南进口道有1条右转车道，有1条直行、左转合用车道.主要道路的中央分隔带有足够的宽度供车辆停靠.

2.1 条件假设

2.2 修正模型推导

马尔可夫过程理论 若某随机过程｛X（t），t∈T｝在某时刻tk所处的状态已知，过程在时刻t（t＞tk）所处的状态只会与过程在tk时刻的状态有关，而与过程在tk以前所处的状态无关，这种特性即称为马尔可夫性.

次要道路排队头车车型为j的出现与所考察的初始时间无关，这正好满足马尔可夫性，因此次要道路排队头车车型的出现就是一个齐次的马尔可夫链.由马尔可夫过程的计算方法可求得次要道路上排队头车车型为j的转移概率zij以及次要道路上排队头车车型为j的平稳分布，进而求得当排队头车的车型是j的出现概率为πj时，次要道路混合车流有k辆车通过交叉的概率pk为

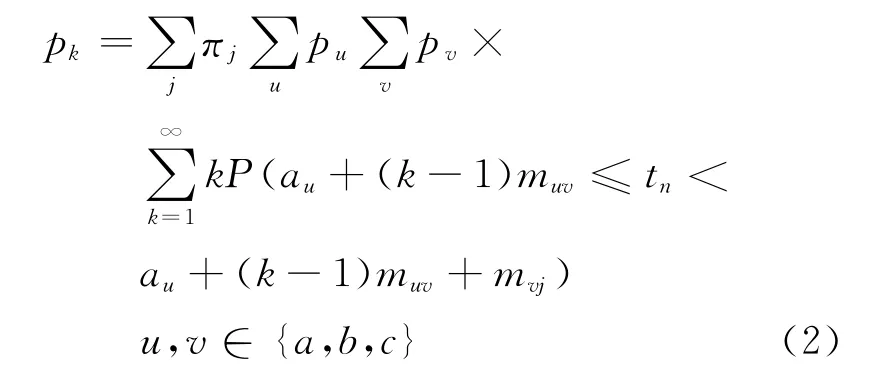
由图2可知，次要道路有左转、直行和右转3路车流.

1）右转情况 当主要道路的西进口道外侧车道提供的可插间隙大于临界间隙时间时，次要道路的车辆即可汇入主要道路.

2）直行情况 当主要道路的西进口道内外侧车道和东进口道内外侧车道同时提供可插间隙均大于临界间隙时间时，可穿越主要道路；当主要道路的西进口道内外侧车道提供可插间隙大于临界时间，而东进口道内外侧车道的车头时距小于临界时间时，车辆在主要道路中央分隔带处停下来等待东进口道内外侧车道可插间隙时间的出现.

3）左转情况 当主要道路的西进口道内外侧车道和东进口道内侧车道同时提供可插间隙均大于临界间隙时间时，可汇入东进口道内侧车道；当主要道路的西进口道内外侧车道提供可插间隙大于临界时间，而东进口道内侧车道的车头时距小于临界时间时，车辆在主要道路中央分隔带处停下来等待东进口道内外侧车道可插间隙时间的出现.

在实际中，左转和直行穿越主要道路的临界间隙时间是不同的，计算该车道的通行能力时，应据概率论按直、左车各占比例进行分析.由于左转车辆对于道路通行能力的影响比较大，下面首先分析左转的通行能力.

西进口道内外侧车道和东进口道内外侧车道同时出现可供k辆车穿越的概率pk1为

西进口道内外侧车道出现可插间隙，而东进口道外侧车道不提供可插间隙的概率pk2为

主要道路西进口道的到达率为λ1，东进口道到达率为λ2，右转车比例为γ，因此左转的通行能力为

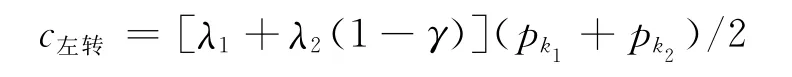
假定次要道路左侧车道车流中，左转车辆与直行车辆的比例为α∶（1－α），则左转的通行能力与直行的通行能力具有如下关系

由次要道路进口道车流到达实际情况，有专家提出在计算次要道路通行能力时，只要知道右转车辆占次要道路车辆的比例即可［12－13］.若假设次要道路上右转车辆占次要道路车流量的比例为β，右转车辆数为x，则有所以x＝因此次要道路的最大通行能力为

由式（3）可知，次要道路的通行能力是与左转车的比例成反比，与右转车的比例成正比，这是因为左转车辆对于直行车辆的影响比较大，而右转车辆在右转专用车道上对直行车辆没有太大影响，正好与实际相符合的.

3 计算实例

某一无信号主路优先控制的交叉口，主要道路车辆的到达符合泊松分布，西进口道到达率为600 pcu／h，东进口道到达率为600 pcu／h，东进口道右转车占该进口道的比例为10%.次要道路现有直左合用车道和右转专用车道两类车道组，通过调查发现各车道组的进口道参数如表3所列.

表3 次要道路进口道车辆构成比例

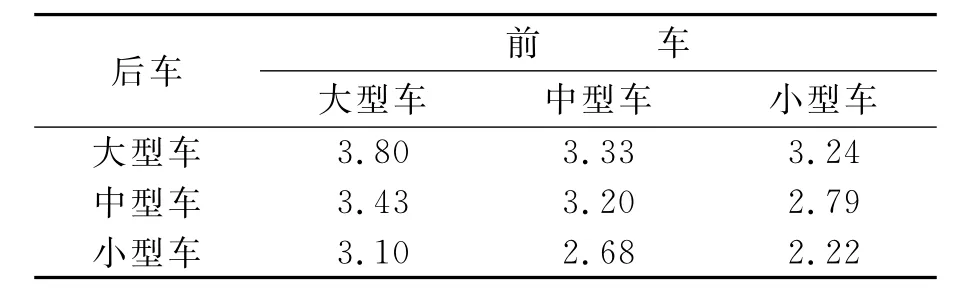
表4 次要道路各种前后车车型组合直行随车时距s

表5 次要道路各种车型多转向临界间隙时间 s

首先，运用理想条件下原模型计算，假设次要道路上的车辆所需穿越的临界车头时距tc＝6 s，车辆跟驰行驶的车头时距tf＝3 s，那么

然后，运用修正后的模型，利用调查参数计算出pk1，pk2和α，代入模型得出直左合用车道的通行能力

当主路交通量增加至2 500 pcu／h时，重新计算pk1和pk2，得出次要道路的通行能力降为37 pcu／h.对不同主路交通量进行计算，理想模型计算值与修正模型计算值的对比情况如表6所列.

次要道路通行能力随主要道路交通流量的变化曲线如图3所示.

表6 理想模型与修正模型计算值的比较 pcu／h

图3 修正模型下主路交通流量对次路通行能力的影响曲线图

由图3可知，在主路交通流量比较小和比较大的情况下，理想模型与修正模型的计算值比较接近，这是因为当主路交通流量很小时，次路车辆穿越交叉口受主路的影响较小；当主路交通流量比较大时，主路的拥挤情况较为严重，供次路车辆穿越交叉口的机会很少.当主路的交通流量在800～2 000 pcu／h时，与理想模型条件下得出的次要通行能力相比较，修正后模型得出的结果更加符合实际情况，这是因为修正模型考虑了不同车型以及次要道路的直左混合车流对于通行能力的影响.

4 结束语

基于可插间隙理论和概率论方法，对理想条件下只有两路车流的主路优先无信号交叉口的次要道路通行能力模型进行了推导，并且运用随机过程的马尔可夫理论，对无信号交叉口主路为双向四车道，次路为直行车、左转车、右转车混合交通流，同时考虑不同车型的次路通行能力进行了理论推导，得到了理论模型.通过计算实例，可发现修正模型得出的结果比理想模型更加符合实际情况，完善了无信号交叉口次要道路通行能力的计算理论.

［1］Sullivan D P，Troutbech R J.The use of cowan＇s M3 head way distribution for modeling ur ban traffic flow［J］.Traffic Engineering Contr ol，1994，27：2－5.

［2］Troutbect R J.Average delay at an unsignalized intersection with two major streams each having a dichotomized head way distribution［J］.Transportation Science，1986，20（4）：272－286.

［3］郭学琴，袁振洲.主路优先控制交叉口的通行能力分析［J］.山东理工大学学报，2006，20（6）：90－92.

［4］钟剑华，吴晓层，简金宝.无信号T型交叉口道路次要道路通行能力分析［J］.交通科技，2006，2：68－70.

［5］刘婷娟，何怀玉.多转向多车型车流通过主路的通行能力［J］.天津师范大学学报，2006，26（4）：62－64.

［6］张建旭，刘 伟.城区无信号交叉口次要道路通行能力计算模型［J］.重庆交通大学学报，2008，27（4）：626－629.

［7］陶经辉，朱翼隽，常玉林.公路无控交叉口混合车流的通行能力［J］.江苏理工大学学报，2001，22（4）：32－35.

［8］李文权，王 炜.无信号交叉口主车流服从移位负指数分布下支路多车型混合车流的通行能力［J］.系统工程理论与实践，2001（2）：122－128.

［9］王 炜，李文权，邓 卫.无信号交叉口多车型混合车流的通行能力［J］.中国公路学报，2000，13（2）：83－86.

［10］沈家军，王 炜，陆 峻.基于支路多车型车流的无信号交叉口等待延误模型研究［J］.土木工程学报，2008，41（4）：86－90.

［11］饭田恭敬.交通工程学［M］.邵春福，译.北京：人民交通出版社，1993.

［12］张起森，张亚平.道路通行能力分析［M］.北京：人民交通出版社，2000.

［13］王殿海.交通流理论［M］.北京：人民交通出版社，2002.