高速公路养护预算定额测定对象的优选方法
丛卓红,吴正莺,郑南翔,李小东
(1.长安大学道路施工技术与装备教育部重点实验室,陕西西安710064;
2.长安大学公路学院,陕西西安710064;3.重庆高速公路集团有限公司,重庆401121)
0 引言
预算定额的测定与编制主要是通过在施工现场中测定施工中消耗的工、料、机数量而实现。一个待测定的依托工程含有多个标段,每个标段同时存在多个施工队组作业。在实际的观测过程中,考虑到由于各施工队组劳动生产水平的差异可能导致结果的可用性差,为避免大量人力物力财力的浪费则需要在众多施工队组中选择合适的观测对象,这是测定定额数据之前必须解决的关键性问题,也是决定采集的数据有效性的重要步骤[1]。笔者采用基于层次分析的模糊综合评价法来进行养护定额测定对象的优选。
1 基于层次分析的模糊综合评价法
模糊综合评价法是一种基于模糊数学的综合评价方法,该综合评价法根据模糊数学隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决难以量化的、模糊的问题,适合各种非确定性问题的解决[2]。
层次分析法的主要思路是将所要分析的问题层次化,根据问题的性质和所要达到的总目标,将问题分解为不同的组成因素,并按照这些因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成一个多层次分析结构模型。最后将该问题归结为最低层相对最高层(总目标)的比较优劣的排序问题[2]。
结合高速公路养护定额测定对象特点,采用基于层次分析法的模糊综合评价法进行优选定额观测对象是一种科学、有效的评价方法。
2 模糊综合评价基本原理与方法步骤
选择的对象好与不好,一般情况下没有固定不变和绝对分明的界限,要从众多个测定对象中选择最优者作为目标,则需要通过多标准来衡量这个目标是否达到,模糊综合评价就是把模糊数学应用到判别事物和系统优劣领域的新方法。
2.1 确定评价对象的因素论域
评价因素即方案受评指标,评价因素论域为:

式中:U为评价因素论域;ui为评价因素(i=1,2,…,n)
测定对象的评价涉及到的因素很多,因此要根据养护单位的实际情况抓住主要因素。笔者通过对各养护公司的调研与专家讨论,确定的各养护分公司的评价因素有养护作业经验、养护机械设备情况、现场管理水平、工人技术水平4个主要方面,测定对象评选系统结构如图1。
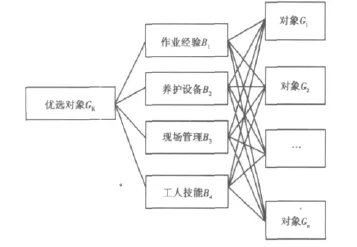
图1 最优对象评选系统结构图Fig.1 Optimal object selection system structure
2.2 确定评价因素的权重
以图1为例,采用层次分析法进行计算,先把评价因素进行两两对比,构成两两对比结果的判断矩阵[3-6]。即


其中:aij>0,aji=1/aij,aii=1(i,j=1,2,3,4,5),aij通常取 1,2,3,4,5,6,7,8,9 及其倒数。

表1 层次分析法因素重要性评判标度Tab.1 Importance evaluation scale of analytic hierarchy process factors
根据判断矩阵A计算其相应最大特征根λmax,ai,使之满足

式中:W 为评价因素的权重向量,W=(w1,w2,w3,w4)T采用和积法求解[6]。对判断矩阵A的每一列正规化:
将A=(aij)n×n按行加总,然后将上一步所得行和向量正规化,得权重向量n1,2,...,n ,再将,求得最大特征值λmax。其中:(AWi)表示A· W的第i个分量,A· W= λmax· W存在。
最后进行一致性检验。
只有当判断矩阵完全一致时,判断矩阵才存在λmax=n;而不一致时,λmax>n。故以λmax-n差值大小来判断一致性程度,用CI这一指标:

其中:λmax为矩阵最大特征根;n为矩阵阶数。CI越小说明一致性越好。同时,必须具有满意的一致性,要将CI与平均随机一致性指标RI比较,得出检验值 CR[5]:CR=CI/RI,RI值见表 2。

表2 平均随机一致性指标Tab.2 Random consistency index of exponential scale
若CR<0.10,视两两对比判断矩阵A的估计基本一致,即认为矩阵的一致性可以接受。若CR≥0.10,视两两对比判断矩阵A的估计不一致,需要重新调整阵A的值,重新估计。
2.3 确定测定对象评价等级
测定对象评价等级应理解为模糊等级,一般可取5个等级,好(Y1)、较好(Y2)、一般(Y3)、较差(Y4)、差 (Y5),其集合为 Y={Y1,Y2,Y3,Y4,Y5}[7]。
2.4 确定各测定对象的复合模糊子集
对于每一测定对象,分别确定其决策模型。

其中:tij为某一测定对象单因素评价下的隶属函数值
综合评价时,采用隶属频率值进行计算[8]。例如:有15位专家对某一养护单位的作业经验进行评价时,有9位评价好,3位评价较好,3位评价一般,则其隶属频率值分别为 0.6,0.2,0.2,0.0,0.0。如此进行可得某一测定对象T,则该测定对象的复合模糊子集为:

其中:p1,p2,p3,p4,p5为该测定对象的最终评价结果。
为了方便计算,引入虚拟分值,根据实际情况需要将各评价等级赋予相应的分值(f1,f2,f3,f4,f5),比如说对等级 Y1,Y2,Y3,Y4,Y5分别赋予(5,4,3,2,1)的分值。则可计算出各测定对象的评价结果虚拟总分如下:

2.5 测定对象的选择
定额编制要满足平均先进性原则。平均先进水平是指在正常的施工条件下,大多数施工队组和大多数生产者经过努力能够达到和超过的水平。一般说它应该低于先进水平,而略高于平均水平,它是编制定额的理想水平。
选择其作业经验、养护设备、现场管理、工人技能等方面的综合模糊评价水平满足平均先进水平的养护单位为养护定额测定对象,由此测定编制的定额水平使先进者感到一定的压力,使处于中间水平的工人感到定额水平可望可及,对于落后工人不迁就,使他们意识到必须花大力气去改善施工条件,提高技术操作水平。按照基于层次分析的模糊综合评价法得到各测定对象的最终评价结果,分别计算量化成的虚拟分值,最后采用二次平均法进行最佳选择,根据实际情况需要,选择若干个与最优测定对象水平相当的养护单位为测定对象。最优对象选择具体步骤如下:
2)将分值高于平均分的测定对象选出(U1,U2,…,Uk),k<n,计算其平均值 h1;
3)计算二次平均值h1=(h+h1)/2;
4)计算Δhi=|hi-h1|,选择满足Δhi最小的对象Gi即为最优测定对象。
3 实例计算
为方便说明,将本例中各养护站分别记为G1,G2,G3,G4。
1)每个养护站的评价因素为作业经验、养护设备情况、现场管理水平、工人技术水平,即评价因素层为Ai=(A1,A2,A3,A4)=(作业经验,养护设备,现场管理,工人技能)。
2)采用层次分析法确定权重。结合实际,通过专家或者决策者来决定判断矩阵的值。各评价因素两两对比,构成两两对比结果的判断矩阵如下:
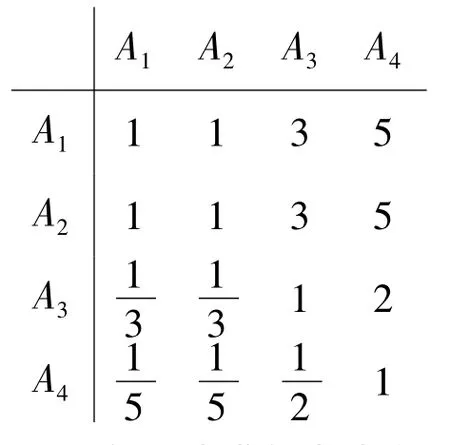
采用和积法求解判断矩阵,计算评价因素的组合权重和最大特征值并进行一致性检验。具体做法是首先求出判断矩阵各列元素之和,再用各列元素分别除以本列元素之和,得出标准化矩阵,然后求出此标准化矩阵各行的平均值,即为该评判因素的权重。λmax的计算是将所得权重与判断矩阵相应列元素相乘,所得矩阵的行和分别与权重相除,所得商的平均值即为特征值。也可以采用MATLAB软件直接计算。得到权重向量为:
W=(0.393 5,0.393 5,0.137 6,0.075 4)T
则λmax的计算过程如表3。

表3 λmax计算过程Tab.3 Calculation process of λmax
则 λmax=(4.007+4.007+4.002+4.000)/4=4.004
最后进行一致性检验:

所以该判断矩阵满足一致性检验,可以接受。
3)确定各测定对象的复合模糊子集
对各分公司 G1,G2,G3,G4,其模糊决策模型见表4。其中隶属函数值的确定针对各个分公司不同的实际情况,收集相关调查资料,通过主观权重法(AHP)和客观权重法(变异系数法)组合赋权决定[9]。

表4 模糊决策模型Tab.4 Fuzzy decision-making model
4)计算综合评价

同理,可计算:


分组,计算 h1=(4.336+4.476)/2=4.406
计算二次平均值:h1=(4.193+4.406)/2=4.299 5
可知 U2-h1=4.336-4.299 5=0.036 5 最小,故,在此选对象2为最优对象。

5)计算虚拟总分

同理,可计算:
U2=4.336,U3=4.173,U4=4.476
6)确定最优对象——计算平均分值
4 结语
在众多的养护单位中如何选择合适的测定对象是测定定额数据之前必须解决的关键问题,也是决定采集的数据有效性的重要步骤[1]。选择合适的高速公路养护定额测定对象对定额编制有着重大的意义。
笔者全面考虑影响优选养护单位的各种因素,建立了评价测定对象的因素论域,运用层次分析法确定了评价对象因素论域中各因素的权重,较好地保证了权重系数的准确性,结合模糊综合评价法,确定各测定对象的复合模糊子集,确定最优对象,选择测定对象范围。应用模糊综合评价法,可以在数据不充分条件下体现评价因素和评价过程的模糊性,同时可以减少因个人主观臆断而带来的弊端,比一般的评价方法更符合客观实际,能够比较客观地评定养护定额各测定对象的实际施工情况,使我们对各测定对象的评价由定性到定量,具有较强的科学性,对实际工程具有一定的指导意义。
[1]李林轶.模糊综合评价在桥涵补充定额编制中的应用研究[D].西安:长安大学公路学院,2009.
[2]汪应洛.系统工程理论、方法及应用[M].北京:高等教育出版社,1998.
[3]慕金波.层次分析法在评定最优环境工程方案中的应用[J].环境科学进展,1997(4):33-40.MU Jin-bo.Application of analytical hierarchy process method for selecting the optimal environmental engineering science[J].Advances in Environmental Science,1997(4):33-40.
[4]孙东生,朱懿,周水兴.基于指数标度的层次分析法在桥梁评定中的应用[J].重庆交通大学学报:自然科学版,2010,29(6):867-870.SUN Dong-sheng,ZHU Yi,ZHOU Shui-xing.Application of exponential scale of AHP in bridge evaluation[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(6):867-870.
[5]Saaty T L.An exposition of the AHP in reply to the paper remarks on the analytic hierarchy process[J].Management Science,1990,36(3):259-268.
[6]曾蓉,陈洪凯,李俊业.熵权模糊综合评价法在公路洪灾危险性评价中应用[J].重庆交通大学学报:自然科学版,2010,29(4):587-591.ZENG Rong,CHEN Hong-kai,LI Jun-ye.Fuzzy comprehensive evaluation method based on entropy in road flood risk assessment[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(4):587-591.
[7]王旭,霍德利.模糊综合评价法在煤矿安全评价中的应用[J].中国矿业,2008,27(5):75-78.WANG Xu,HUO De-li.Application of fuzzy comprehensive evaluation in coal safety assessment[J].China Mining Magazine,2008,27(5):75-78.
[8]何夕平.模糊综合评价在选择最优施工方案中的应用[J].合肥工业大学学报:自然科学版,2000,23(6):1050-1054.HE Xi-ping.Application of fuzzy comprehensive evaluation to selecting the optimal construction plan[J].Journal of Hefei University of Technology:Natural Science,2000,23(6):1050-1054
[9]李玉琳,高志刚,韩延玲.模糊综合评价中权值确定和合成算子选择[J].计算机工程与应用,2006,23(5):38-43.LI Yu-lin,GAO Zhi-gang,HAN Yan-ling.The determination of weight value and the choice of composite operators in fuzzy comprehensive evaluation[J].Computer Engineering and Application,2006,23(5):38-43.

