钢箱拱肋吊杆锚固结构受力分析

吕成林，安永日，郑 罡

(1.重庆交通大学土木建筑学院，重庆400074;2.招商局重庆交通科研设计院有限公司，重庆400067)

下承式钢箱系杆拱桥，因具有良好的受力性能、跨越能力大、工期短、施工方便等优点，在桥梁建设中得到广泛的应用。该桥型在跨越高等级公路、铁路及河流的桥梁中具有较好的优越性。又因造型美观，也常用于城市、风景区的桥梁建设。

目前，国内学者已对下承式钢箱系杆拱桥进行了一些研究。如:孟杰［1］研究了系杆拱桥的结构体系;顾安邦，等［2］分析了中、下承式拱桥短吊杆结构行为;曾德荣，等［3］研究了拱肋内倾角对提篮式拱桥横向稳定性影响;郭建勋，等［4］分析了结构形式和设计参数;甘进［5］分析了结构动力特性及其抗震性能;刘山洪［6］研究了系杆拱桥系杆锚下有效索力;叶梅新［7］、余山川［8］研究了拱脚局部结构;屈志峰［9］对该种桥做了 1∶8全桥模型试验研究;叶梅新［10］、王月［11］研究了该类桥的稳定性;王月［11］对拱脚、吊杆与拱肋连接处、吊杆与系梁、横梁连接处等关键部位进行了局部受力分析。

以上学者虽然对该种桥梁的整体受力特性及关键部位做了大量研究，并阐明了整体结构及局部构造的受力性能，但是针对钢箱拱肋吊杆锚固结构研究比较少，其受力机理尚不明确。笔者结合江津滨江新城滨州路一号桥，采用有限元软件，对不同构造形式的吊杆锚固结构进行了数值模拟分析。通过分析，了解了各种不同吊杆锚固结构的受力机理以及传力特性。结果表明，吊杆与拱肋中心线夹角的变化对锚固结构的极限承载力影响微小，其刚度变化趋势基本相同，而圆管与拱肋底板连接形式对其影响较大。

1 工程概况

江津滨江新城滨州路一号桥是重庆市江津区滨洲路上的一座重要的城市桥梁。其桥型为主跨120 m的下承式钢箱系杆拱桥。拱肋为钢箱结构，跨径120 m，计算矢高37.2 m，矢跨比 1/3.2。拱肋截面如图1。截面为箱型等截面，拱肋高2.8 m，宽1.8 m。顶、底板厚度均为32 mm，腹板厚度为24 mm。吊杆与拱肋中心线夹角从44～90°变化。吊杆与拱肋锚固连接处由拱肋顶板、底板、腹板，横隔板、加劲肋，圆管等组成。

图1 拱肋截面Fig.1 Arch rib cross-section

2 局部模型与计算方法

2.1 局部模型

局部模型取受力最不利的节段，即拱脚处第1根吊杆以及拱顶处的吊杆锚固结构。为了提高计算效率对结构进行适当简化，钢箱拱肋计算长度取标准长度8 m。

钢箱拱肋吊杆锚固结构模型如图2。根据吊杆与拱肋中心线夹角不同和圆管与底板有无连接，将局部模型分为4种。

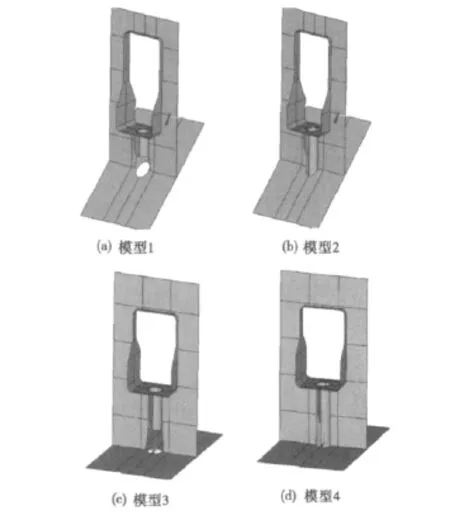
图2 局部模型Fig.2 Partial model diagram

计算模型类型如表1。模型1是吊杆与拱肋中心线成44°，圆管与拱肋底板未连接;模型2是吊杆与拱肋中心线成44°，圆管与拱肋底板连接;模型3是吊杆与拱肋中心线成90°，圆管与拱肋底板未连接;模型4是吊杆与拱肋中心线成90°，圆管与拱肋底板连接。

表1 计算模型分类Tab.1 Computational model classification

数值模拟计算软件采用 ANSYS，单元采用SHELL181板壳单元。材料采用Q345D钢材，其弹性模量取 2.1 ×105MPa，泊松比取 0.3，屈服强度345 MPa，硬化率为 0。

2.2 计算方法

计算方法采用材料弹塑性以及几何非线性理论，应用弧长法进行计算。

2.3 边界条件以及加载方法

计算模型以拱肋轴向为x轴，横桥向为y轴，竖向为z轴。其模型边界条件为:约束拱肋前端部截面的x、y、z轴方向位移及绕x轴转角，约束拱肋后端部截面的y轴方向位移，z轴方向位移。

加载方法为锚垫板与螺母重叠处节点与圆管中心节点刚臂连接，并在圆管中心节点上施加吊杆方向的荷载。

3 计算结果

3.1 极限承载力

吊杆锚固结构局部模型极限承载力计算结果如图3。图中x轴表示锚固结构加载点的位移，y轴表示加载点的荷载与最大索力的比值。

图3 吊杆锚固结构加载点荷载/索力－位移Fig.3 Load and cable force displacement of the loading point

1)考察4个模型的极限承载力，模型1的极限承载力为最大索力的2.33倍，模型2的极限承载力为最大索力的2.83倍，模型3的极限承载力为最大索力的2.33倍，模型4的极限承载力为最大索力的2.90倍，其值均大于公路桥涵钢结构与木结构设计规范［12］中的安全系数 1.7。

2)比较模型1与模型2，其结果如图3(a)。模型2的极限承载力为模型1的1.21倍，大于模型1。其主要原因为模型2圆管与供肋底板连接成整体，拱肋底板多承担了部分荷载，而模型1圆管与底板未连接，底板承担的荷载小。再比较两者的刚度，在弹性阶段，模型1与模型2刚度基本相等。随着荷载的持续增加，模型1的刚度退化比模型2快。其原因为模型2中圆管与底板连接成整体，底板多承担了部分荷载。

3)比较模型1与模型3，其结果如图3(b)。两者的极限承载力基本相等。由此可见，吊杆与拱肋中心线夹角的变化对吊杆锚固结构的极限承载力影响不大。再比较两者的刚度，在弹性阶段，模型1的刚度比模型3略大，随着荷载的持续增加，结构逐渐进入塑性阶段，模型1的刚度退化比模型3稍微早点。其原因为模型1吊杆与拱肋中心线的夹角为44°，拱肋底板承担了部分荷载，而模型3夹角为90°，底板不承担荷载，所以模型1初始刚度比模型3大。

4)比较模型3与模型4，其结果如图3(c)。模型4的极限承载力是模型3的1.25倍，大于模型3。其原因为模型4圆管与底板连接成整体，拱肋底板多承担了部分荷载，而模型3圆管与底板未连接，所以其极限承载力比模型4小。再比较两者的刚度，在弹性阶段，模型3与模型4刚度相差不大;随着荷载的持续增加，模型3的刚度退化比模型4快。其原因为模型4中圆管与底板连接成整体，底板多承担了部分荷载。

5)比较模型2与模型4，其结果如图3(d)。模型4的极限承载力是模型2的1.03倍，两者相差微小，与图3(b)中模型1和模型3的趋势基本相同。

3.2 应力分布

局部模型计算结果的von Mises应力分布变形图分别如图4、图5。图4是荷载达到最大索力时应力分布情况，图5是加载结束时的应力分布情况。

1)比较模型1与模型2，荷载达到最大索力时其应力分布如图4(a)、(b)。模型1的最大等效应力为324 MPa，出现在锚垫板边上以及下方横隔板的小部分截面上，其他大部分截面的应力均小于容许应力209 MPa。模型2的最大等效应力为337 MPa，比模型1略大，出现的位置与模型1相同。其他大部分截面的应力均小于容许应力209 MPa。模型1、模型2拱肋底板与横隔板连接区域应力为10～75 MPa，应力水平均较低。

比较模型1与模型2，加载结束时的其应力分布如图5(a)、(b)。模型1锚垫板、圆管部分截面以及周边横隔板部分截面及其加劲肋部分截面已经屈服。模型2的应力分布趋势与模型1基本相同，只是塑性区域比模型1大。此外，两者底板的应力分布不同。模型2中圆管与拱肋底板连接区域的截面也已经屈服。

2)比较模型1与模型3，荷载达到最大索力时其应力分布如图4(a)、(c)。模型3的最大等效应力为344 MPa，比模型1大，出现的位置与模型1相同。其他大部分截面的应力均小于容许应力209 MPa。两者拱肋底板与横隔板连接区域应力为10～77 MPa，应力水平均较低。

比较模型1与模型3，加载结束时的应力分布如图5(a)、(c)。模型3的应力分布趋势与模型1基本相同，只是两者底板的应力分布不同。

3)比较模型3与模型4，荷载达到最大索力时其应力分布如图4(c)、(d)。模型4的最大等效应力为324 MPa，比模型3小，出现的位置与模型3相同。其他大部分截面的应力均小于容许应力209 MPa。两者拱肋底板与横隔板连接区域应力为13～77 MPa，应力水平均较低。

比较模型3与模型4，加载结束时的应力分布如图5(c)、(d)。模型4的应力分布趋势与模型3基本相同，只是塑性区域比模型3大。此外，两者底板的应力分布不同。

4)比较模型2与模型4，荷载达到最大索力时其应力分布如图4(b)、(d)。模型2的最大等效应力为337 MPa，模型4为324 MPa，比模型4略大。两者最大等效应力出现的位置基本相同，而其他大部分截面的应力均小于容许应力209 MPa。两者拱肋底板与横隔板连接区域应力均低72 MPa，应力水平较低。

比较模型2与模型4，加载结束时的应力分布如图5(b)、(d)。模型2、模型4的应力分布趋势基本相同，只是两者底板的应力分布不同。模型2圆管与拱肋底板连接区域的截面也已经屈服。

3.3 结构变形

加载结束时，4个模型结构的变形如图5。

1)比较模型1与模型2，模型1吊杆锚固位置处横隔板两侧的加劲肋向内侧屈曲变形，拱肋腹板也向内屈曲变形，拱肋底板向下发生屈曲变形。模型2结构变形的趋势与模型1基本相同，但是拱肋底板与圆管连接处屈曲变形大，圆管下端受压发生膨胀变形。模型2的变形比模型1大。

2)比较模型1与模型3，模型3结构变形的趋势与模型1基本相同，两者的变形差不多，只是模型3拱肋底板发生微小褶皱变形。

3)比较模型3与模型4，模型4结构变形的趋势与模型3基本相同，但是拱肋底板与圆管连接处屈曲变形大，圆管下端受压发生膨胀变形。模型4的变形比模型3大。

4)比较模型2与模型4，模型2结构变形的趋势与模型4基本相同，两者的变形差不多，只是模型4拱肋底板发生微小褶皱变形。

4 结论

通过对不同构造形式吊杆锚固结构的数值模拟分析得到以下结论:

1)4个模型的极限承载力与最大索力的比值，均大于公路桥涵钢结构与木结构设计规范中安全系数 1.7。

2)比较吊杆与拱肋中心线角度44°的锚固构造的极限承载力，圆管与拱肋底板相连构造为无连接构造的1.21倍。其原因为圆管与拱肋底板相连接，底板多承担了部分荷载。

3)比较吊杆与拱肋中心线角度90°的锚固构造的极限承载力，圆管与拱肋底板相连构造为无连接构造的1.25倍。其原因为圆管与拱肋底板相连接，底板多承担了部分荷载。

4)比较圆管与拱肋底板相连构造与无连接构造的屈服区域和变形，相连构造大。

5)吊杆与拱肋中心线夹角的变化对锚固结构极限承载力的影响微小。

6)比较吊杆与拱肋中心线角度44°的锚固构造的刚度变化，在初始阶段圆管与拱肋底板相连构造与无连接构造基本相同。随着荷载的持续增加，无连接构造的刚度退化的比有连接构造早。

［1］孟杰.系杆拱桥结构体系研究［D］.长沙:湖南大学，2002.

［2］顾安邦，徐君兰.中、下承式拱桥短吊杆结构行为分析［J］.重庆交通学院学报，2002，21(4):1-3.GU An-bang，XU Jun-lan.Behavior analysis of short boom structure of half-through and through arch bridge［J］.Journal of Chongqing Jiaotong University，2002，21(4):1-3.

［3］曾德荣，张庆明.提篮式拱桥拱肋内倾角对横向稳定性的影响［J］.重庆交通学院学报，2006，25(增刊1):4-5.ZENG De-rong，ZHANG Qing-ming.The influence on lateral stability of the inclination angle of arch rib of basket arch bridge［J］.Journal of Chongqing Jiaotong University，2006，25(supp1):4-5.

［4］郭建勋，袁明，陈列，等.福厦铁路钢箱系杆拱桥设计构思与研究［J］.桥梁建设，2006(增刊2):97-100.GUO Jian-xun，YUAN Ming，CHEN Lie，et al.Concept design and research on steel-box tied arch bridge of Fuzhou-Xiamen railway［J］.Bridge Construction，2006(supp2):97-100.

［5］甘进.钢箱系杆拱桥动力特性及抗震性能分析［D］.武汉:武汉理工大学，2007.

［6］刘山洪.系杆拱桥系杆锚下有效索力研究［J］.重庆交通学院学报，2007，26(1):1-4.LIU Shan-hong.Effective cable force when the tie rod anchored of tied arch bridge［J］.Journal of Chongqing Jiaotong University，2007，26(1):1-4.

［7］叶梅新，李一可.下承式钢箱系杆拱桥拱脚局部受力分析［J］.西部探矿工程，2007(7):165-169.YE Mei-xin，LI Yi-ke.Partial stress analysis at abut of through arch steel-box tied bridge［J］.West-China Exploration Engineering，2007(7):165-169.

［8］余山川.武广客运专线140m钢箱系杆拱桥拱脚模型试验研究［D］.长沙:中南大学，2009.

［9］屈志峰.武广客运专线大跨度下承式钢箱系杆拱桥试验研究［D］.长沙:中南大学，2008.

［10］叶梅新，王月，周德.横向连接系对下承式钢箱系杆拱桥稳定性的影响［J］.黑龙江科技信息，2008(30):225-227.YE Mei-xin，WANG Yue，ZHOU De.Influence on stability of through arch steel-box bridge for horizontal connections［J］.Heilongjiang Science and Technology Information，2008(30):225-227.

［11］王月.140m下承式钢箱系杆拱桥关键部位局部受力分析［D］.长沙:中南大学，2009.

［12］JTJ 025—86公路桥涵钢结构及木结构设计规范［S］.北京:人民交通出版社，1988.