用波浪辐射动量应力分析波浪减水现象

张耀屹，徐绩青，许锡宾

(重庆交通大学河海学院，重庆400074)

波浪辐射应力的概念是由Longuet-Higgins和Stewart提出的，他们在牛顿流体力学定理和速度沿水深均匀分布假定的基础上，将波浪辐射应力定义为由于波浪现象而产生的动量超通量［1］;可见辐射应力只是一种通俗的称谓，它是被平均在水深上的力，并不能完全体现流场中流体具体某一点的应力。

雷诺输运方程表明:一个物质体系内某种流体广延量的增长率，等于体系在该时刻所占的那个空间区域中同一物理量的增长率加上单位时间内由区域边界流出的该物理量的总通量;进而雷诺输运方程导出的流体动量方程探索出:在空间的一个固定区域中，单位时间内流体总动量的增加，等于该时间内通过区域边界面进入区域的动量(包括由于流体进出该区域所携带的动量的净增量和由于表面力作用传递到区域内的动量)，加上在外场力作用下引起的区域内流体动量的改变［2］。

通过对以上2组概念的对比，不难看出可以运用雷诺输运方程求出由于波浪现象而产生的动量超通量，进而表示出波浪的辐射应力张量。

1 辐射动量应力的产生

1.1 传统辐射应力张量的表达式及应用［3－5］

1.1.1 传统辐射应力张量的表达式

通常，辐射应力的张量表达式为:

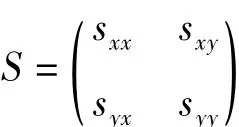
式中:sxx表示作用在垂直于x轴平面的x方向的剩余动量流，称作辐射应力在x方向上的主分量;syy表示作用在垂直于y轴平面上的y方向的剩余动量流，称作辐射应力在y方向上的主分量;sxy表示作用在垂直于x轴平面上的y方向动量流，称作辐射应力在垂直于x轴平面上的切向分量;syx表示作用在垂直于y轴平面上的x方向的动量流，称作辐射应力在垂直于y轴平面上的切向分量。以不同的波理论的水质点速度及波压力公式可以计算得到不同的辐射应力表达式。据微幅波理论，波向角为α时辐射应力的张量形式表达式为:

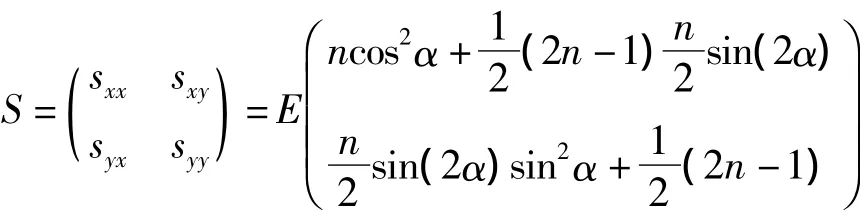
1.1.2 传统辐射应力张量推导的减水方程

用传统的辐射应力公式求得规则波的减水方程为:

式中:A为波浪振幅;k为波数;h为水深。

1.2 “辐射动量应力”张量的表示

1.2.1 理论探讨

Longuet-Higgins和Stewart将作用于单位面积水柱体的总动量流的时均值减去无波浪作用时的静水压力定义为波浪剩余动量流，又称作辐射应力［1］。而实际上，由雷诺输运方程出发推出动量流ρvivj才是真正的应力张量。沿整个控制体的外表面做曲面积分，得到的是一个合力，这才是“辐射应力”的本质特征。由于:

1)动量流的周期时均值仍然是一个张量(其变换法则不受时间的影响);

根据传统辐射应力的概念，结合雷诺输运方程，定义:辐射动量应力=-动量流+反向应力;由此可见:辐射动量应力是一个真正的应力张量。其表达式可表示为:

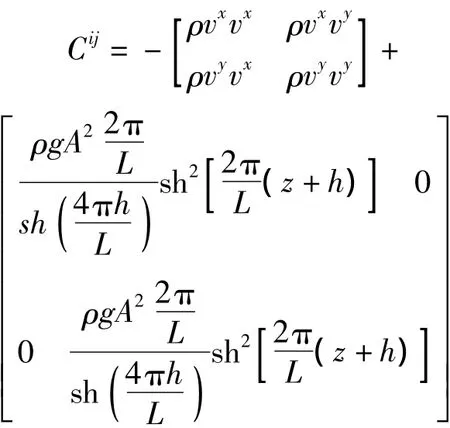
即:

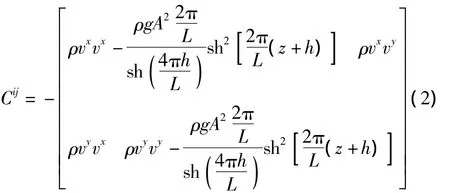
式中:ρvivj为动量流的应力张量分量为反向应力的张量表达式。

1.2.2 公式证明［2，6-7］

静水压力的曲面积分(对坐标)已与控制体的重力抵消，对于二阶斯托克斯波的作用，静水压力曲面积分等于控制体的重力，如图1。

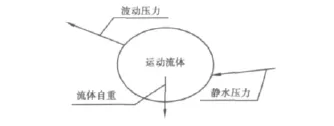
图1 任意运动流体质点受力Fig.1 Arbitrary exercise fluid particles stress

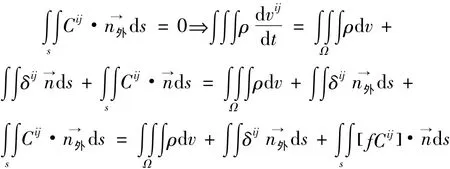
从动量流出发得到的该方程符合积分形式的动量方程，还可变为微分形式的运动方程，从而得出“辐射动量应力”张量表达式(2)，式(2)在流体中的确发挥的是辐射应力的作用。

2 用“辐射动量应力”求解减水方程

“辐射动量应力”在海岸动力学中的应用，即波浪增减水方程的求解。

波浪增减水方程可以看成沿岸流方程的特例，沿x方向(见图2)的沿岸流方程:

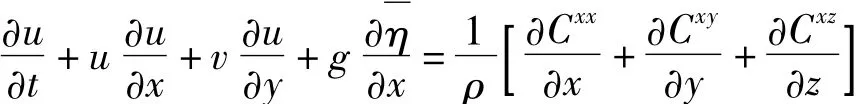
其中:Cij为“辐射动量应力”，对应二阶斯托克斯波(pij为反向应力)。

这时，假定u=0，平直海岸情况下波高在沿岸方向均匀一致，即u与项均为0。沿岸流方程可简化为:

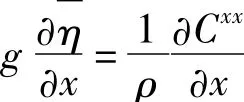
因为，波浪沿x方向传播，即Cxy=0，Cxz=0，那么此方程在本质上仍然表现为波浪正向传播时所产生的增减水作用，即

因为，二阶斯托克斯波的时均水面下降η*，所以波动压力的时均值取z'为坐标原点，即:

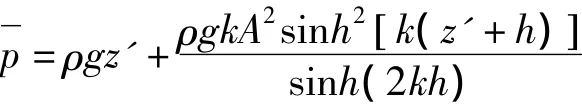
破波带外:

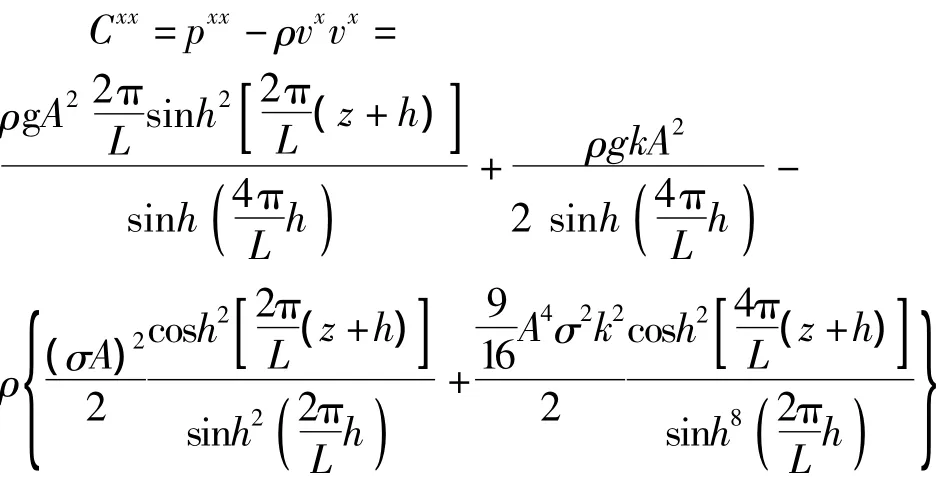
整理得:

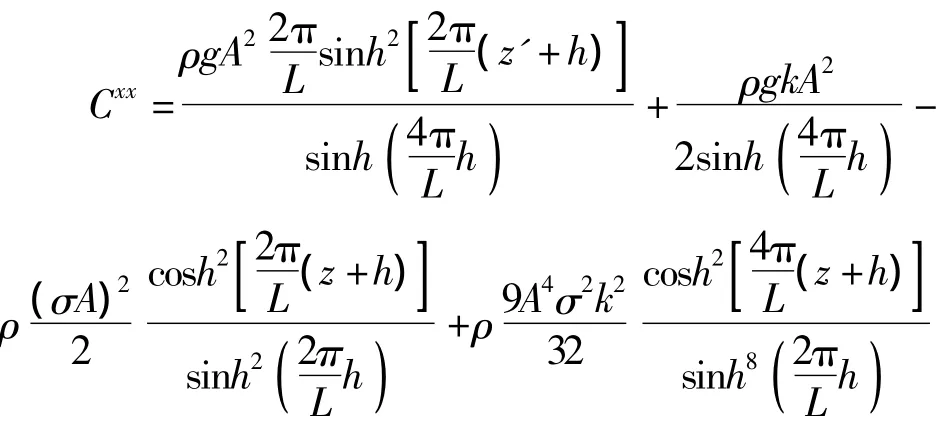
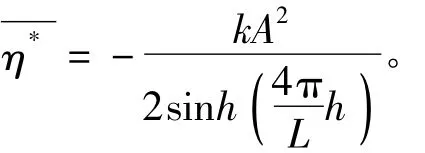
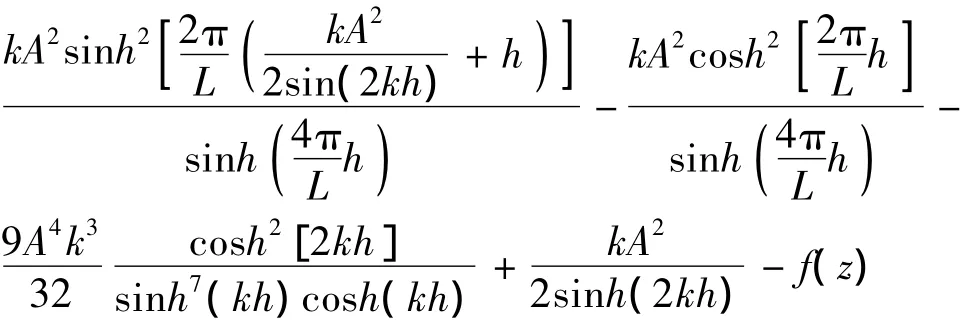
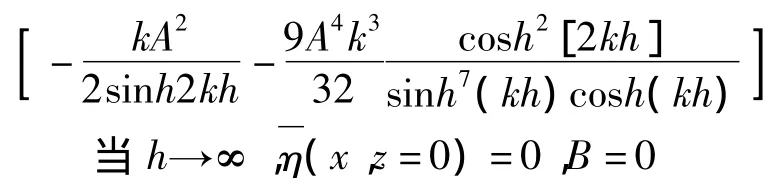
综上所述:

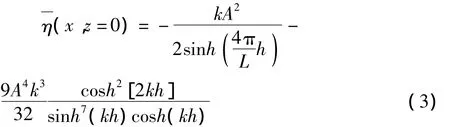
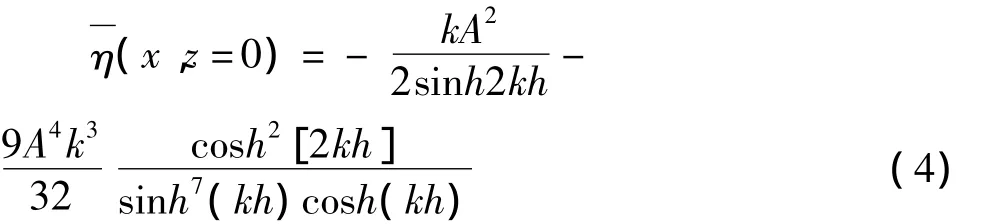
由此可见，以上用“辐射动量应力”求解的减水方程的结果式(4)忽略掉高阶无穷小量后与用传统辐射应力张量算出的减水方程的结果式(1)形式上是一致的;另外，式(4)比式(1)多了一个高阶无穷小的修正量值，理论上增强了运算结果的可靠性。

3 结论

1)用波浪辐射动量应力分析波浪减水现象，推导出的减水方程与传统辐射应力张量计算出的结果基本吻合，具有可靠性。

2)相对于传统概念的“辐射应力”，“辐射动量应力”具有明显的优越性。它体现的是真正的应力张量;张量各分量沿水深的变化一目了然;作用力的计算比较简单;概念非常清楚，体现了力学本源;拓展了辐射应力的适应范围，传统的辐射应力概念在牛顿流体力学定理和速度沿水深均匀分布假定的基础上建立的，而本表达式没有相关的限制。

3)运用辐射动量应力还可来求解波浪的增水方程和探寻沿岸流的生成机理。

［1］Longuet-higgns M S，Stewartr W.Radiation stresses in water waves:a physical discussion with application［J］.Deep Sea Resarch，1964，11(5):529-562.

［2］庄礼贤，尹协远，马晖扬.流体力学［M］.合肥:中国科学技术大学出版社，1991:83-89.

［3］马锡超，卜令涛，王璇.辐射应力理论在近岸区的应用及其研究进展［J］.海岸工程，2008，27(1):73-77.MA Xi-chao，BU Lin-tao，WANG Xuan.Radiation to the application in the stress theory and its research progress inshore coastal engineering［J］.Coastal Engineering，2008，27(1):73-77.

［4］邹志利.海岸动力学［M］.北京:人民交通出版社，2010:107-122.

［5］温秀媛.波浪辐射应力计算及其对低频波浪的影响［D］.大连:大连理工大学，2009.

［6］郑永红，沈永明，邱大洪.结合抛物型缓坡方程计算波浪辐射应力［J］.海洋学报，2000，22(6):110-116.ZHENG Yong-hong，SHEN Yong-ming，QIU Da-hong.Combined wave radiation stress calculation with Parabolic mild-slope equation［J］.Acta Oceanologica Sinica，2000，22(6):110-116.

［7］郑金海，严以新.波浪辐射应力张量的垂向变化［J］.水动力学研究与进展，2001，16(2):246-253.ZHENG Jin-hai，YAN Yi-xin.The Wave radiation stress tensor vertical change［J］.Journal of Hydrodynamics，2001，16(2):247-254.

［8］李孟国，王正林，蒋德才.近岸波浪传播变形数学模型的研究与进展［J］.海洋工程，2002，20(4):43-57.LI Meng-guo，WANG Zheng-lin，JIANG De-cai.Offshore wave propagation of deformation mathematical model research andprogress［J］.Maritime Engineering，2002，20(4):43-57.

［9］林祥，尹宝树，侯一筠，等.辐射应力在黄河三角洲近岸波浪和潮汐风暴潮相互作用中的影响［J］.海洋与湖沼，2002，33(6):615-621.LIN Xiang，YIN Bao-shu，HOU Yi-jun，et al.Radiation stress in the Yellow River delta offshore wave and tidal storm surge of interaction effects［J］.Oceanologia and Limnologia Sinica，2002，33(6):615-621.

［10］蔡晓禹，凌天请，唐伯明，等.波浪对散体岸坡冲刷破坏的机理［J］.重庆交通学院学报，2006，25(2):73-76.CAI Xiao-yu，LING Tian-qing，TANG Bo-ming，et al.The waves to scour the damage mechanism of Loose material accumulation［J］.Journal of Chongqing Jiaotong University，2006，25(2):73-76.