电站锅炉声学测温中扫频信号声源特性研究
安连锁, 李庚生, 张世平, 沈国清, 冯 强, 邓 喆
(华北电力大学电站设备状态监测与控制教育部重点实验室,北京 102206)
现代电站燃煤锅炉参数的日益提高,对炉内燃烧状况的监测提出了更高的要求.获得准确的炉内温度场对精确监测锅炉的燃烧与运行状况具有十分重要的意义.国内外的学者对温度场监测的方法进行了研究和探索,声学法作为其中一种非接触性测温方法,能适应高温、腐蚀和多尘的恶劣环境,并且可以实现连续实时监测[1].对于电站锅炉这种大空间、强噪音的工作环境,声源的选择至关重要.在声波飞渡时间的测量中,张晓东等[2]提出了基于互相关的方法,并对扫频信号的互相关性做了简单研究;杨祥良等[3]对电声源做了试验研究,表明电声源因其构造简单、技术成熟的优势可以用于声学测温.笔者借助声学测温实验台,在实验室条件下对不同频段的扫频信号进行了研究,并且在国内某300 MW电站锅炉上进行了热态试验.
1 声学测温原理
图1为单路径声学测温示意图.声波信号由炉膛左侧测点的声波发生器发出,被左右两侧的接收器测到,通过声波飞渡时间的测量,可以用来确定声波在传播路径上的平均速度.根据平面波的运动方程、平面波的波动方程以及气体状态方程推导出声波测温的原理方程[4-5]如下:

式中:τ为声波飞渡时间,s;L为测点距离,m;c为介质中声波的传播速度,m/s;R为理想气体普适常数,J/(mol◦k);t为气体温度,℃;γ为气体的绝热指数(定压比热容与定容比热容之比值);m为气体分子量,kg/mol.

图1 单路径声学测温示意图Fig.1 Schematic diag ram of the one-path acoustic temperature measurement
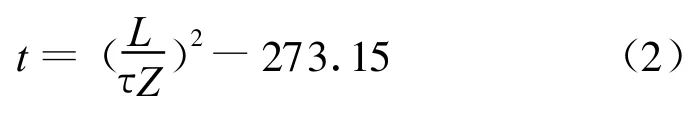
2 扫频信号及互相关时延估计法
2.1 扫频信号
扫频信号的形式通常有三种,分别是对数扫频、线性扫频和二次扫频,表1给出了三种扫频信号的数学模型.表1中:f0为0时刻点扫频信号的瞬时信号频率;f(τg)为τg时刻点扫频信号的瞬时频率;[0,τg]为信号的持续时间.
扫频信号可以对最大旁瓣值产生抑制,其相关函数具有很好的尖锐性,能有效降低互相关最大值点的错误判断,提高测量的准确性.
罗振[6]对不同的扫频信号进行了仿真研究,表明线性扫频信号在不同的信噪比下测量的误差最小,优于对数扫频信号和二次扫频信号,因此笔者采用线性扫频信号作为声源信号.

表1 三种典型的扫频信号Tab.1 Mathematical models for three typical chirp signals
2.2 互相关时间延迟估计法
声波飞渡时间的测量采用互相关时间延迟估计法.两通道的信号模型为[7]:

式中:s(n)为信号函数;n1(n)和n2(n)为噪声函数;D为两通道间的时间延迟;A表示衰减系数.直接互相关函数为[8-9]:

时间延迟估计为:
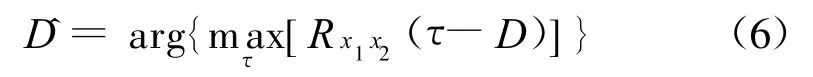
间接法互相关函数为:
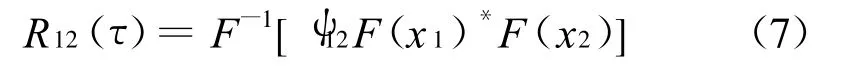
式中:ψ12为频域处理的加权函数;F为傅里叶变换;F-1为傅里叶逆变换;*表示共轭.本文中采用间接法求互相关函数,取加权函数为1.
3 实验室试验结果与分析
笔者在实验室条件下,对不同频段的扫频信号进行了试验研究.首先由主机中的SpectraLAB软件发出线性扫频信号,经声卡转换为模拟信号后,再经过功率放大器放大输出至扬声器,驱动扬声器发射出测温声波信号.信号采集和分析系统为NI公司多通道数据采集卡,软件系统采用LABVIEW和MAT LAB软件进行混合编程.传声器采用的是1/2英寸预极化驻极体无指向性测量传声器MPA201(灵敏度50 mV/Pa),属电容式结构.
从文献[10]可以看出,互相关函数测量声波飞渡时间,产生误差与锅炉背景噪音、采样点数及采样频率有关.在具体的工程应用中,由于测量距离比较大,采样频率可取在104量级以上.文献[11]表明,当采样点数取512,1024和 2048时,只要采样频率满足条件,都能有效测得精确的飞渡时间.
取采样频率为102400 Hz,采样点数为65536,试验温度15℃,测得当地声速为340.5 m/s.两只传声器之间的距离为2.96 m,则计算得到的声波飞渡时间为8.6931 ms.实验室处于相对安静的环境,无明显噪声影响.
3.1 扫频信号频率区间的选择
首先采用扫频周期为0.1 s,设定起始频率为500 Hz,选取了10组不同截止频率X的线性扫频信号发声进行声波飞渡时间的测量,每组测量20次.
表2和图2给出了声波飞渡时间测量值与计算值的平均绝对误差MAE和相对均方根误差RRMSE,其计算公式如下:
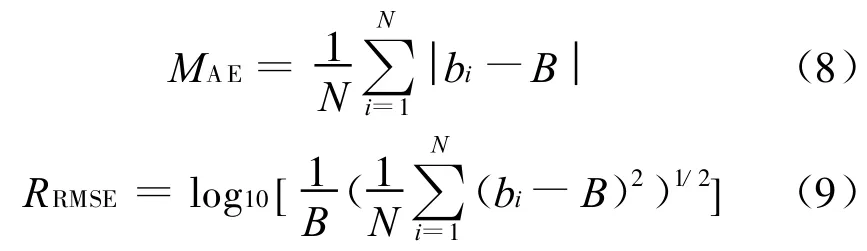
式中:N为试验次数;bi为第i次试验得到的测量值;B为理论计算值.
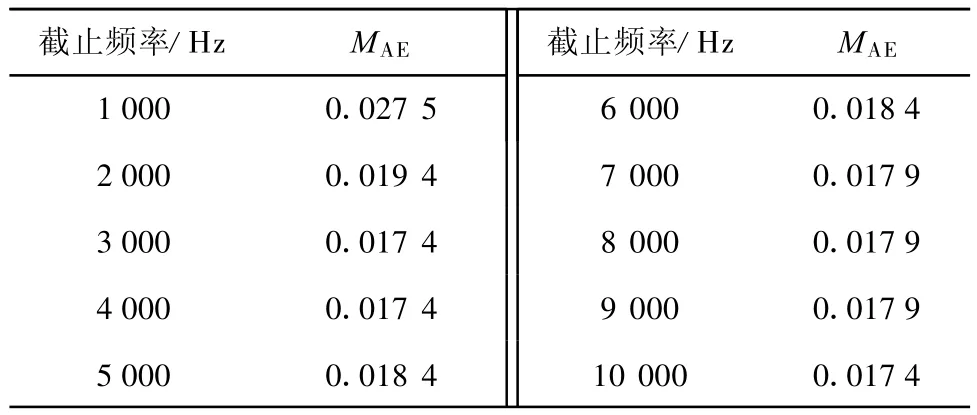
表2 起始频率500 Hz,不同截止频率时的 MAE(单位:ms)Tab.2 MAEof calculated results and actual measurements for chirp signals with frequency(Hz)from500 to X
图2给出了测量值与计算值的相对均方根误差及误差趋势线.可以明显看出,随着截止频率X增大,相对均方根误差递减.
图3给出扫频区间(Hz)为[500,8000]时的互相关图,其互相关函数具有明显峰值.研究表明,随着X的增大,对应的互相关图中互相关函数的峰值越来越尖锐,测量效果越来越好.

图2 起始频率500 Hz,不同截止频率时的 RRMSEFig.2 RRMSEbetween calculated results and actual measurements for chirp signals with frequency from 500 to X(Hz)

图3 扫频区间(Hz)为[500,8000]时的互相关图Fig.3 Cross correlation chart of chirp signal with frequency from 500 to 8000(Hz)
取扫频周期为0.1 s,截止频率设为8000 Hz,选取7组不同起始频率Y对声波飞渡时间进行测量.表3和图4为测量值与计算值的平均绝对误差MAE和相对均方根误差RRMSE.
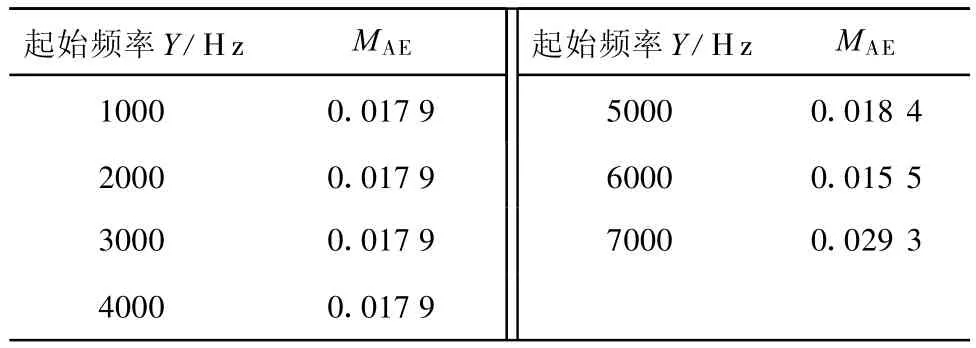
表3 截止频率8000 Hz,不同起始频率时MAE(单位:ms)Tab.3 MAEbetween calculated results and actual measurements for chirp signals with frequency(Hz)fromY to 8000

图4 截止频率8000 Hz,不同起始频率时的相对均方根误差Fig.4 RRMSEbetween calculated results and actual measurements for chirp signals with frequency(Hz)from Y to 8000
从图4可以看出,扫频区间(Hz)为[Y,8000],随着Y的增大,RRMSE有增大的趋势.试验表明,随着起始频率的升高和区间间隔的减小,其互相关函数图的峰值变得不再明显.图5给出了扫频区间(Hz)为[7000,8000]时的互相关图,此区间内峰值已基本无法分辨.

图5 扫频区间采样点为[7000,8000]Hz时互相关图Fig.5 Cross correlation chart of chirp sig nal with frequency from 7000 Hz to 8000 Hz
选取扫频周期0.1 s,扫频区间间隔为3000 Hz,分别对其声波飞渡时间进行测量.图6给出了部分测量得到的互相关图.分析可知,随着频率的增高,相同区间间隔互相关图中互相关函数的峰值越来越不明显.

图6 扫频区间间隔为3000 Hz部分互相关图Fig.6 Cross correlation charts of chirp signals with a frequency interval of 3000 Hz
3.2 扫频周期的选择
选取扫频区间(Hz)为[500,8000],扫频周期(s)分别取 0.01、0.05、0.06、0.07、0.08、0.09、0.10、0.20、0.30 、0.40 、0.50 、0.60 和 0.80,计算其平均绝对误差,结果见表4.
图7给出了不同扫频周期下线性扫频信号的相对均方根误差.从图7可以看出,0.05 s到0.80 s的扫频周期中,相对均方根误差变化不大,0.10 s和0.20 s附近具有较小的RRMSE.

表4 不同扫频周期下的平均绝对误差(单位:ms)Tab.4 MAEbetween calculated results and actual measurements for chirp signals in different cycles(unit:ms)

图7 不同扫频周期下测量值与计算值的相对均方根误差Fig.7 RRMSEbetween calculated results and actual measurements for chirp signals in different cy cles
4 300MW锅炉现场试验研究
4.1 热态试验
在国内某300 MW锅炉机组34.5 m平台上安装声学测温系统,在其前墙和后墙布置测点,测点距离为13.59m.定义发声端传声器所在通道为通道1,接受端传声器所在通道为通道2.设置采样频率为102400 Hz,采样数为65536,发声频率(Hz)为[500,8000],此时锅炉负荷为230 MW.
图8给出了锅炉热态测量的波形图,图中纵坐标PSD为功率谱密度.可以明显看出,在没有滤波的情况下,通道2接收的扫频信号波形严重失真,这主要是由于锅炉本底噪声很大,声源信号完全淹没于其中.图8(c)和图8(d)给出了通道1和通道 2接收到的声源信号和炉膛本底噪声信号混合频谱图,混合声的能量大部分集中在500~3000 Hz频率段,线性扫频信号能量也主要集中在低频段,高频段能量相对较小.大量研究表明,锅炉炉膛本底噪声主要集中在1000 Hz以下,设置滤波区间为[1000,5000]Hz,通过滤波处理,通道2的扫频信号波形显现出来.图8(h)给出了滤波后通道2的信号频谱图,这时的声音能量主要集中在[1000,3000]Hz区间,3000 Hz以上的声音几乎衰减殆尽.
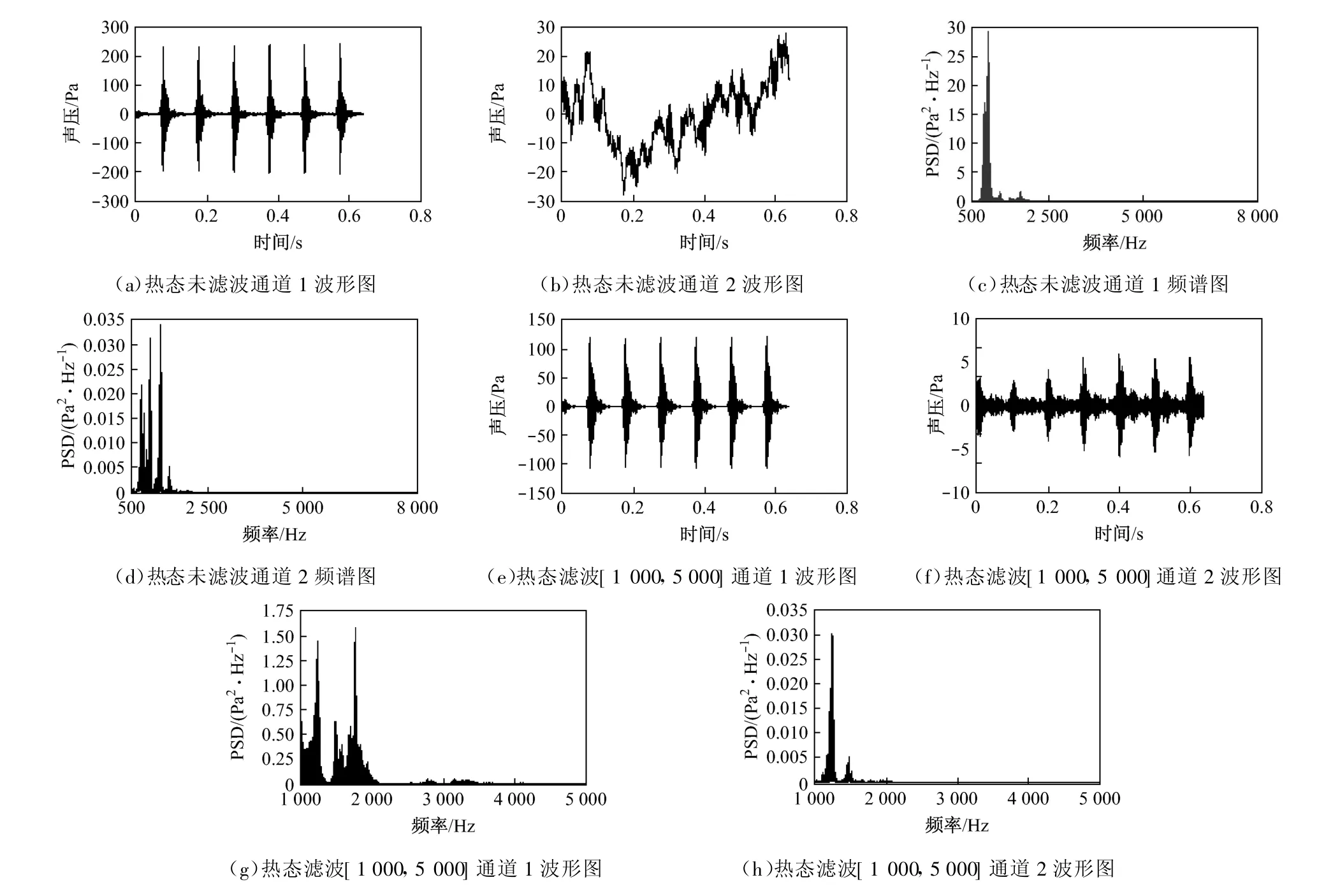
图8 300MW锅炉热态试验时部分波形图Fig.8 Wavefo rms obtained in hot-state experiments for a 300 MW boiler
综合冷态试验分析,最后确定扫频发声区间取为[500,3000]Hz,扫频周期为0.1 s,滤波区间为[1000,3000]Hz,利用声学法对烟气温度进行测量,测量结果见表5.

表5 声学法测量得到的烟气温度Tab.5 Actual measurements of gas temperature by acoustic pyrometry ℃
图9给出了热态测量时的互相关图,峰值较为明显也相当稳定.测量结果中,第6次和第8次发生明显错误,第1、2、3、4、7和9次的测量数据相对准确.为了证实测量的准确性,在测量的同时采用热电偶进行标定.
4.2 温度标定
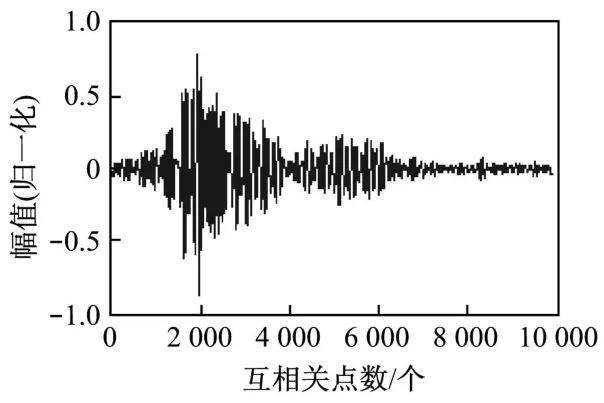
图9 300M W锅炉热态滤波[1000,3000]Hz互相关图Fig.9 Cross correlation chart of chirp signals with filtering frequency from 1000 to 3000(Hz)

图10 热电偶温度标定示意图Fig.10 Schematic diagram of temperature measurement with thermocouple
定制加工了长约5 m的k型加厚不锈钢铠装热电偶,精度为±1 K,测量示意图见图10.分别将热电偶从声波发射端、声波接收端插入炉膛,改变不同的插入深度,每个测点20 min左右达到热平衡.炉墙外侧温度200℃左右,炉墙内侧450℃左右.热电偶插入深度超过0.5 m时,温度梯度较大,从200℃直接上升到1000℃;超过0.5 m以后,基本稳定在1000~1200℃.热电偶分别从发射端和接收端插入,温度值由热电偶读数表读出,冷端补偿自带.
图11为热电偶测量温度变化图.整个测量路径的平均温度为1072℃,与采用声学测温得到的结果基本相同,表明声学测温系统测量的温度满足要求.

图11 热电偶测温标定温度图Fig.11 Temperature distribution measured with thermocouples
5 结 论
(1)线形扫频信号作为电站锅炉声学测温的声源信号是完全可行的.
(2)在相同的扫频间隔中,起始频率和截止频率越高,效果越差.
(3)扫频信号随着扫频周期的变化有着不同的测量效果,研究表明扫频周期取0.1 s为宜.
(4)电站锅炉温度场声学监测中,声源扫频信号区间间隔越小,效果越差,考虑到热态的衰减效应,声源信号扫频区间取[500,3000]Hz为宜.
(5)在锅炉热态中,噪声基本上淹没了接收端声源信号,但是噪声频率较低,可以通过滤波滤除,滤波区间根据锅炉情况加以选择.热态混响影响较小,滤波后有较好的测量效果,但测量不是非常稳定.热态声波衰减规律及时间延迟算法还待进一步研究.
[1]田丰,邵富群,王福利.基于声波的工业炉温度场测量技术[J].沈阳航空工业学院学报,2001,18(3):10-11.TIAN Feng,SHAO Fuqun,WANG Fuli.An introduction to measuring technique on temperature field for industrial boiler based on acoustic wave[J].Journal of Shenyang Institute of Aeronautcal Engineering,2001,18(3):10-11.
[2]张晓东,高波,宋之平.互相关函数法在声学测温技术中的应用研究[J].中国电机工程学报,2003,23(4):185-188.ZHANG Xiaodong,GAO Bo,SONG Zhiping.The research of acoustic measuring of gas temperature employing cross-correlation algorithm[J].Proceedings of the CSEE,2003,23(4):185-188.
[3]杨祥良,安连锁,沈国清,等.单路径声学高温计实时监测锅炉炉膛烟温的试验研究[J].动力工程,2009,29(4):379-383.YANG Xiangliang,AN Liansuo,SHEN Guoqing,et al.Experimental study on real-time monitoring of flue gas temperature in boiler furnace by one-path acoustic pyrometer[J].Journal of Power Engineering,2009,29(4):379-383.
[4]KLEPPE J A,NENO R.New method and apparatus for measuring acoustic wave velocity using impulse:USA,5349859[P].Sep 27,1994.
[5]沈国清.声学方法重建炉内温度场的算法研究[D].保定:华北电力大学能源动力与机械工程学院,2004.
[6]罗振.炉膛燃烧噪音环境下声波飞行时间测量方法研究[D].沈阳:沈阳航空工业学院,2006.
[7]陈昶,陈玮,邓则名,等.管道泄漏检测中自适应时间延迟估计方法的设计[J].工业仪表与自动化装置,2003,(6):26-28.CHEN Chang,CHEN Wei,DENG Zeming,et al.The design of adaptive time delay estimation algorithm for pipeline leak detection[J].Industrial Instrumentation&Automation,2003(6):26-28.
[8]周洁,袁镇福,岑可法,等.光信号互相关测量两相流中颗粒流动速度的研究[J].中国电机工程学报,2003,23(1):185-187.ZHOU Jie,YUAN Zhenfu,CENG Kefa,et al.Measurement of particle velocity in two-phase flow by optical cross-correlation method[J].Proceedings of the CSEE,2003,23(1):185-187.
[9]向阳.基于互相关延时估计的波速估计方法[J].武汉理工大学学报(信息与管理工程版),2003,25(5):63-66.XIANG Yang.An evaluation method for wave speed in concrete based on a cross-correlation function[J].Journal of Wuhan Automotive Polytechnic University,2003,25(5):63-66.
[10]张波,安连锁,沈国清,等.互相关函数在声学测温系统中的误差分析[J].电力科学与工程,2006(1):45-47.ZHANG Bo,AN Liansuo,SHEN Guoqing,et al.Error analysis of acoustic pyrometer based on crosscorrelation method[J].Electric Power Science and Engineering,2006(1):45-47.
[11]刘立云,田丰,李治壮,等.基于互相关技术的声波飞行时间测量系统的设计与实现[J].沈阳航空工业学院学报,2005,22(1):57-60.LIU Liyun,TIAN Feng,LI Zhizhuang,et al.Design and realization of the acoustic waves flight time measurement system based on cross-correlation method[J].Journal of Shenyang Institute of Aeronautcal Engineering,2005,22(1):57-60.

