移动平均线在合肥市肺结核疫情监测预警中的应用

陈伟

移动平均法就是将数据按照时间排列,以一定的跨越期进行移动平均得出平均值进行预测的一种方法。该方法能够消除时间序列中的偶然因素对预测结果的影响,突出反映趋势性和周期性的变动,适用于一年期等短期预测,现已被广泛应用于各种疾病及医院统计预测中。本研究探讨如何采用Excel函数的方法计算移动平均数(预测值),并绘制移动平均线,进行肺结核疫情预警分析。

资料与方法

一、数据来源

疾病监测信息报告管理系统中,报告日期为2006—2009年以及2010年上半年,报卡中患者现住址为合肥市(统计对象不限制患者户籍所在地)的肺结核数据。

二、方法

1.基础数据处理

将已收集的报告日期为2006—2009年以及2010年上半年报卡现住址为合肥市的肺结核报告数据进行整理,去除已删除卡、结核性胸膜炎及其他疾病,保留疾病诊断为涂阳、菌阴、未痰检3类肺结核已终审卡数据。

在传染病监测预警分析中,目前一般以周为单位,步长采用2(即数据统计时变动范围为前后2周)为宜[1]。因此,对整理后的2006—2009年数据,按照报告日期,划分为全年52周,列出每周报告肺结核患者数,形成基础数据表。

2.指标分类和意义

根据基础数据表数据,按照周次和每周患病数,将2006—2009年4年数据形成患病数数列,利用Excel函数,计算该数列的残差、标准差和回归曲线方程(W=(其中W 为预测值为截距,μα为斜率,Si为预测年份累积周次),利用得到的回归方程,代入预测年份(第5年)的累积周次,即第 209～260周(1年有52周,第5年为209～260周),得出的数据,即是预测年每周的预测患病数,并继续计算2倍标准差(预警值)、3倍标准差(行动值),根据数据绘制相应的线图。

正常情况下,实际预测年份每周患病数应在预测值的上下进行波动。当实际值超过预警值时,提示该周患者数超过预期,应予以关注,分析导致病例突然增高的原因,实施干预;当实际值超过行动值时,应立刻分析原因,判断是否局部疫情暴发,立即采取干预措施,控制疫情的发展。

3.统计学处理

将预测值数列利用K-S检验方法进行检验,取得Z值和P值,按α=0.05检验水准判断数据资料是否符合正态分布。如符合正态分布,再用t检验比较2010年上半年实际值数列和预测值数列之间的差异是否具有统计学意义,从而判断合肥市的肺结核疫情资料是否符合移动平均分布。

结 果

一、计算回归方程

利用Excel表格计算2006—2009年每周患病数数列的回归方程：W=-0.25Si+116.26,其中 W 为预测值,Si为预测年份累积周次,即第209～260周。

回归方程相关数据见表1。

二、计算预测值、预警值和行动值

利用得到的回归方程,代入预测年份(第5年)的累积周次(即第209～260周),得出的数据,即是预测年每周的预测患病数(预测值),并继续计算每周患病数的2倍标准差为预警值,3倍标准差为行动值。详细数据见表2。

三、移动平均线图制作

将预测值、预警值、行动值3个系列数据填充至Excel数据表格中,绘制预警监测图。将2010年每周患病数录入后,形成实际周患病数曲线,通过实际周患病数曲线在预测曲线、预警曲线、行动曲线之间的波动范围,即可开展预警工作(详细图形判读见方法中的指标分类和意义)。

四、预测数据拟合检验

1.将预测值数列利用K-S检验方法进行检验,得Z值为0.774,P=0.586,按α=0.05检验水准可认为数据资料符合正态分布。

表1 回归方程数据

表2 合肥市2006—2009年肺结核周患病数情况及2010年预警分析

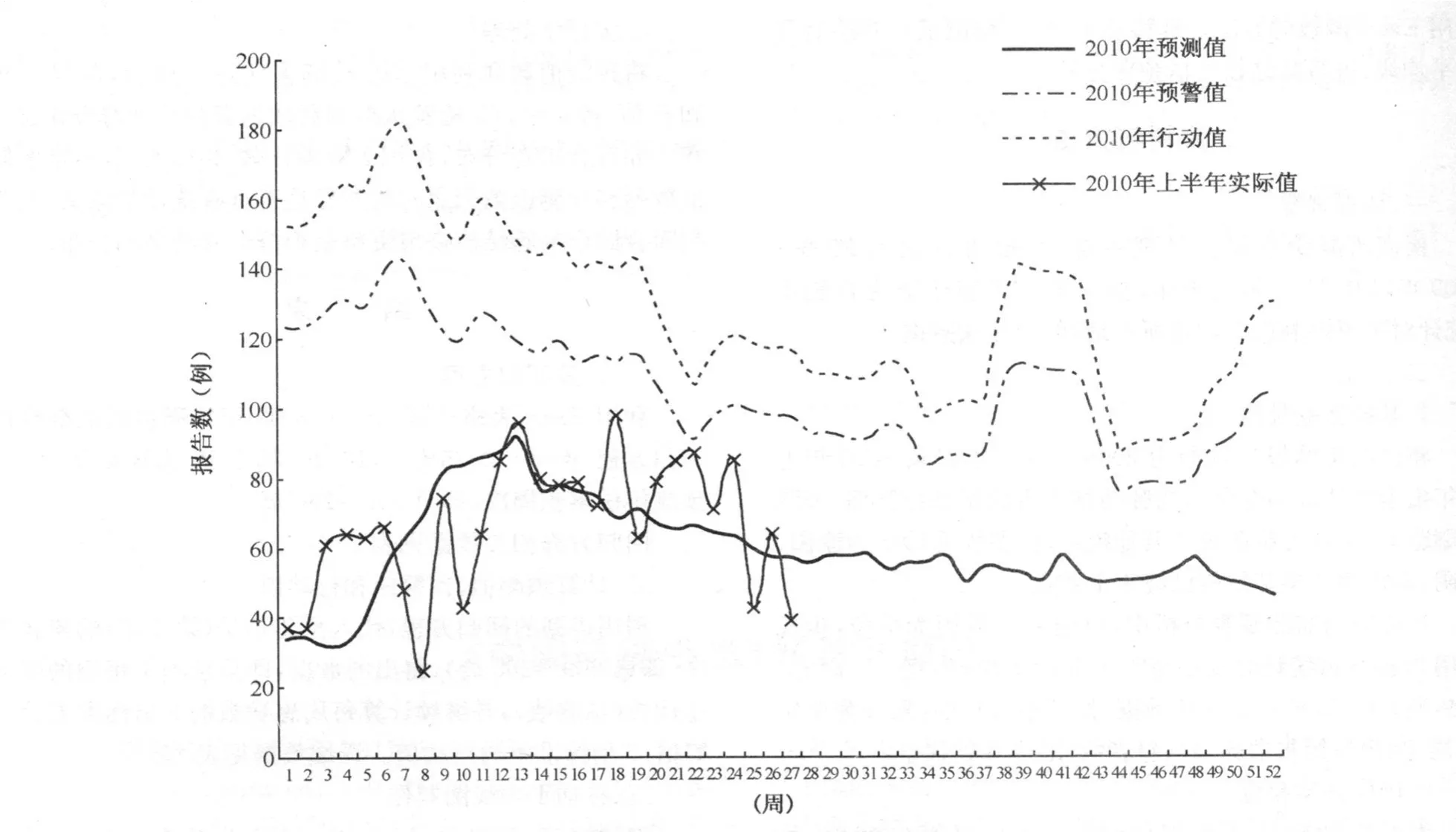
图1 2010年合肥市结核病疫情预测图

2.用t检验比较2010年上半年实际值数列和预测值数列之间差异是否具有统计学意义。得t(双尾)值为2.02,P=0.07＞0.05,按α=0.05检验水准可认为,2010年上半年实际报告组和预测组之间差异无统计学意义,预测值数列构成的移动平均线与实际疫情曲线拟合一致,能够反映实际疫情发展的趋势,可认为合肥市的肺结核疫情资料符合移动平均分布。

讨 论

基线数据是决定预警效果的重要因素。自2005年以后,我市肺结核疫情呈显著下降趋势,在这种情况下,疫情预测基础数据时间太长,会大大降低预警的敏感性[3]。所以,笔者选择2006—2009年4年作为基础数据时间,并以大疫情终审报卡为数据来源校正漏报率,以涂阳、菌阴、未痰检三类疾病诊断校正病例定义的改变,同时去除删除卡避免错误统计,保证基线数据的真实可靠。

为解决因数据数量可能偏少,一些统计指标的计算和数据模型的稳定性有可能受到影响的问题,美国疾病预防控制中心作预警时,将预警时间单位向前和向后各移动2个单位,数据量增加,并证明这种处理方法是可行的[4]。本研究借用了这个方法,将2007年的原前2周数据,同时作为2006年的第53周和 54周数据;将 2006年的 51、52两周数据作为2007年的前2周数据。以此类推,从而将每年的观察周数增加至54周,并且可有效避免各年份之间人为划分时间段对数据分析结果带来的影响。

通常移动平均线期限愈长,愈能表现安定的特性,即移动平均线不轻易波动,必须趋势真正明朗了,移动平均线才会延伸。而这恰恰符合肺结核疫情长期趋势稳定的特征：每年第13周左右为高峰期,后逐渐下降,至次年的第4周左右达到低谷。因此,采用移动平均线评价合肥市肺结核疫情的趋势较为合适。

移动平均线主要依据某一时期及其相邻时期内的时间序列数据的算术平均值数列进行绘制,因此存在数据惯性问题,即在疫情暴发早期监测数据逐步抬升过程中,存在着滞后效应,对疫情的早期发现不敏感。这点必须引起疫情预警监测人员的高度重视,可考虑采用求和自回归移动平均(ARIMA)模型的方法提高早期预警的灵敏度。

[1]仝振东,林君芬,陈国水,等.应用移动平均数法开展传染病疫情监测预警的探讨.疾病监测,2007,22(8)：523-525.

[2]胡跃强,庞志峰.移动平均数在金华市痢疾疫情监测预警中的应用.现代预防医学,2008,35(10)：1809-1010.

[3]杨维中,邢慧娴,王汉章,等.七种传染病控制图法预警技术研究.中华流行病学杂志,2004,25(12)：1039-1041.

[4]Costagliola D, Flahaul t A , Galin ec D, et al . A routine tool fordetect ion and assessment of epidemics of influenza-like syndromesin France. Am J Public Health , 1991 , 81(1)：97-99.