泥沙颗粒相对隐蔽度在散体沙起动研究中的应用
孟 震,杨文俊
(长江科学院水利部江湖治理与防洪重点实验室,武汉 430010)
泥沙颗粒相对隐蔽度在散体沙起动研究中的应用
孟 震,杨文俊
(长江科学院水利部江湖治理与防洪重点实验室,武汉 430010)
运用泥沙隐蔽度的研究成果,结合泥沙起动的滚动模型,导出了以隐蔽度为参数的泥沙近底作用起动流速公式。通过对该式分别进行的极限分析和单调性分析,论述了散体沙起动的几个物理现象,论证了宽级配非均匀沙的起动特性。经过对泥沙颗粒隐蔽度分布特性及泥沙起动标准的分析,建立了泥沙颗粒隐蔽度与无因次起动切应力之间的数值关系。最后借鉴前人的研究成果,验证了本文公式的适用性。
隐蔽度;起动;极限;单调性;起动条件
1 概 述
泥沙起动研究已有200多年的历史,研究前期主要针对散体均匀沙,如较著名的“六次方定律”和Shields无因次临界拖拽力[1]等。这一时期对泥沙起动的处理方法一般分为3个步骤:①把泥沙颗粒概化为球体,忽略粒间作用力和粘结力;②通过对泥沙颗粒受力分析,建立滚动起动、滑动起动或跳跃起动方程,并推求泥沙近底作用起动流速;③采取某一水流流速分布来建立近底作用流速与垂线平均流速的关系,或者把近底作用流速转化成无因次临界起动切应力。
散体均匀沙的起动研究总体上还是比较成熟的,但是对散体非均匀沙的起动研究仍存在很多困难,至今起动公式仍没有统一的形式。一般来讲,散体非均匀沙起动的研究方法主要体现在4个方面[2]:①取宽级配非均匀沙中某一级配泥沙做代表,直接代入散体均匀沙的起动(流速、切应力、功率等,下同)公式;②引入一个附加力(阻力、动力及质量力),建立泥沙起动平衡方程,推求出具有一定物理意义的起动公式(秦荣昱、张启卫等);③通过研究颗粒的绝对暴露度,建立被“增大”或“减小”后的等效粒径,并代入起动平衡方程推求泥沙起动公式(刘兴年等);④研究颗粒的相对暴露度,分析泥沙颗粒的起动力臂和阻力臂,进而推求出以相对暴露度为参数的起动公式(韩其为等)。从上述中间的2种研究方法中,我们不难得到宽级配非均匀沙的起动特性:粗颗粒较之同粒径的均匀沙易于起动,细颗粒较之同粒径的均匀沙难于起动,中等粒径泥沙颗粒与同粒径的均匀沙起动条件相当[1,2]。
本文拟从3个方面来研究泥沙颗粒相对隐蔽度在散体沙起动中的应用:①借鉴韩其为的研究思想,建立以相对隐蔽度为参数的散体沙近底作用起动流速公式;②结合非均匀沙颗粒相对隐蔽度的研究成果,数学上论证宽级配非均匀散体沙的起动特性;③分析起动标准及相对隐蔽度分布特性,数值上建立散体沙起动临界切应力与相对隐蔽度在不同起动标准下的对应关系。以下所述隐蔽度若无特殊说明均表示泥沙颗粒相对隐蔽度。
2 泥沙颗粒隐蔽度
如图1所示,参考前人的研究方法[2],将颗粒概化为二维“圆饼”状。泥沙颗粒隐蔽度为床面上所研究表层泥沙颗粒的最低点到与下游颗粒接触点之间沿床面的垂向距离(隐蔽长度)与所研究颗粒粒径的比值,记为η。并定义1-η为泥沙颗粒的暴露度,记为ξ。研究表明[3]:对于均匀沙来讲,统计意义上隐蔽度的取值区间为[0.067,0.5];对于非均匀沙讲,任意级配粒径颗粒隐蔽度的期望的计算式为
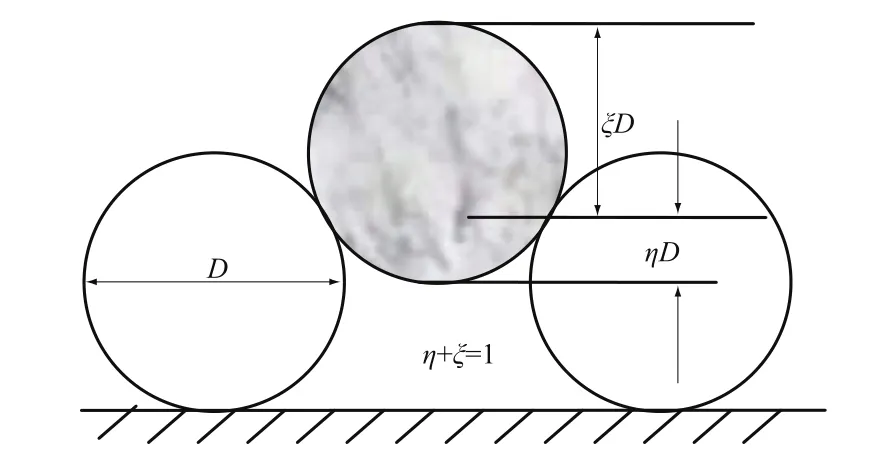
图1 泥沙颗粒暴露度、隐蔽度示意图Fig.1 Exposure and hidden degree of sediment
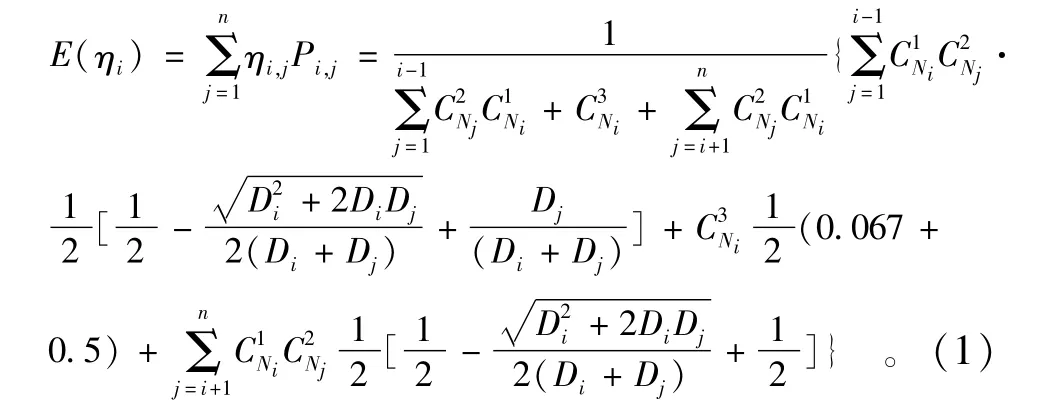
式中:ηi,j为颗粒Di在颗粒Dj影响的综合隐蔽度;Pi,j为对应组合的概率;Ni为颗粒Di在表层床沙中的粒数。
3 泥沙起动公式
3.1 泥沙颗粒水下受力及力矩分析
泥沙起动流速(切应力)是一个瞬时量,所研究的泥沙颗粒是表层床沙,也就是说所建立的泥沙起动公式仅仅适合“第一层”床沙。对于床面表层的散体沙,可以忽略粒间作用力和粘结力。水下泥沙颗粒所受力一般为水流拖拽力、水流升力(脉动上举力)、水下重力。若忽略渗流梯度力的影响,可把泥沙受力、泥沙起动力矩和阻力矩的相关表达式列成表1。

表1 泥沙颗粒水下受力及力矩表达式Table 1 Equations for the force and moment of underwater sediment particles
3.2 近底作用起动流速
如图2所示,根据表1中的表达式,我们可以建立粒径为Di的泥沙颗粒滚动起动模型的力矩平衡方程Md=Mf,即
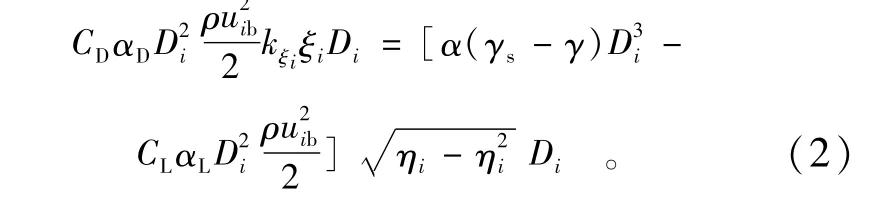
其中,ξi+ηi=1,可以解得
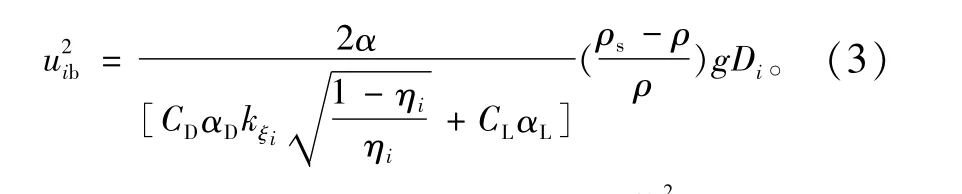
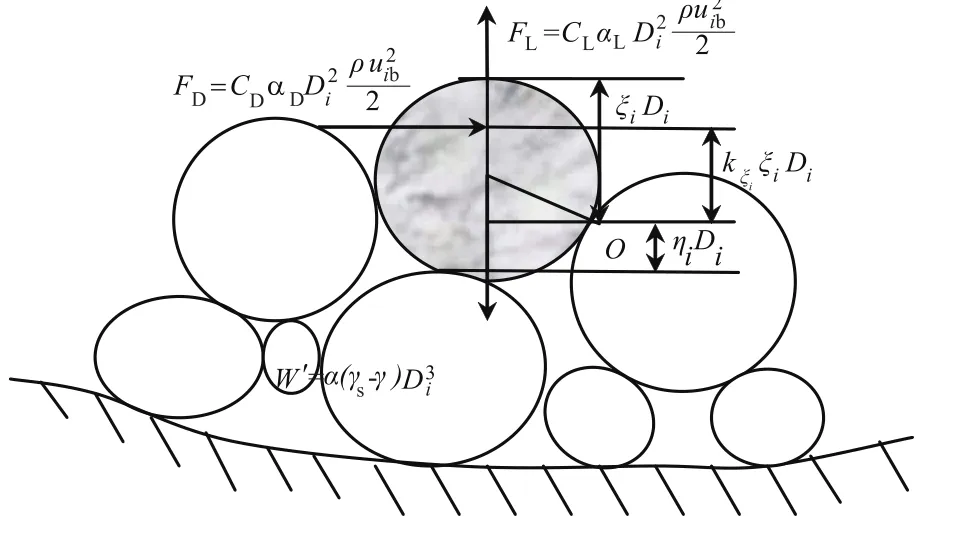
图2 泥沙颗粒水下受力图Fig.2 Forces of underwater sediment particles
3.3 水流推力力臂系数
理论上讲,可以从2个角度来解决该系数的取值问题:①经验计算,即借鉴韩其为对特征高度的经验取值,等价于本文利用的水流推力有效力臂,可以求出该系数;②数值计算,即利用微积分计算出泥沙颗粒所受的水流力矩及推力,二者的比值为水流推力的有效力臂。
3.3.1 经验计算
根据韩其为的研究思想,假定水流推力作用点距球心上方1/6直径处,这样就得到
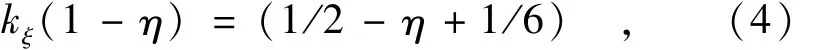
解得kξ=1-1/3(1-η)。代入均匀沙隐蔽度的期望0.283 5[3],这样得到均匀沙水流推力力臂修正系数kξ=0.534 8。
3.3.2 数值计算
对于推移质泥沙颗粒来讲,河床上泥沙颗粒起动后,仍将“下落”(滚落、滑落、沉落)到河床的“凹槽”处,等待下次起动。当所研究颗粒与下游颗粒发生碰撞(或向下游颗粒翻越)时,可以忽略下游颗粒对其隐蔽性的影响,该模型可近似概化为光滑平板上单颗粒起动(见图3)。当所研究颗粒“下落”到下游“凹槽”处时,下次起动时,要考虑下游颗粒对其隐蔽作用的影响(见图4)。于是要分2种情况来研究水流推力力臂系数:
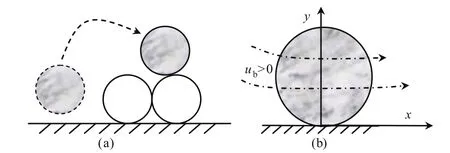
图3 碰撞力作用下的水流推力力臂系数计算图解Fig.3 Calculation of arm-of-force coefficient by flow thrust under collision force
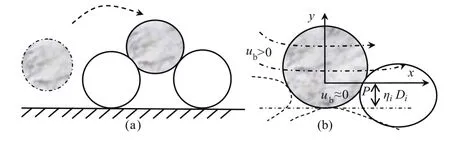
图4 床面形态影响下的水流推力力臂系数计算图解Fig.4 Calculation of arm-of-force coefficient by flow thrust under the effect of the bed form
(1)不受床面形态影响下的单颗粒起动。该模型考虑了颗粒间碰撞力的作用,此时可以忽略下游颗粒的影响,该模型可概化为光滑平板上单颗粒起动。根据对泥沙颗粒的“面积元”进行积分来求解其力矩及受力可得
这里的流速采用指数型流速分布公式,指数m取6[2],可以计算出kξ≈0.550。
(2)受床面形态影响下的单颗粒起动。该模型考虑了颗粒间隐蔽度的作用,忽略水流在泥沙隐蔽长度范围内水流速度(孔隙流)的影响,同理可以计算出水流推力力臂系数,
代入均匀沙隐蔽度的期望0.283 5[3]及流速分布指数m=6,可以计算出kξ=0.509 1。耦合上述2种模型,可取泥沙颗粒水流推力力臂系数为式(5)与式(6)的平均值0.530。可以发现这2个角度得出的结论是基本一致的。当推力力臂系数越大泥沙越容易起动,为提高泥沙起动条件的预测精度,可以确定水流推力力臂系数为0.530。对于宽级配非均匀沙来讲,由于任意级配颗粒的隐蔽度受床沙级配特性的影响[3],无法在数值上构建出任意级配粒径颗粒的水流推力力臂修正系数。但可以定性分析:由于较大颗粒的隐蔽度期望较小,依照上述计算方法,对应的水流推力力臂系数要略大于0.53;小颗粒对应的水流推力力臂系数要略小于0.53。为统一研究宽级配非均匀沙的分级起动,可假定宽级配非均匀沙水流推力力臂系数的平均值与均匀沙水流推力系数相等。
4 起动公式分析
研究泥沙隐蔽度的目的是为更好地解决泥沙起动流问题,以往人们对泥沙颗粒隐蔽度的分析都是在统计意义上进行的,即泥沙颗粒隐蔽度要小于0.5。事实上,床面泥沙确实存在一些极端情况,在分析文中所推求的泥沙颗粒近底作用起动流速公式之前,首先给出3点说明:
(1)统计意义上来讲,泥沙起动为泥沙输移初始阶段,河床泥沙在水流的作用下自动组织成稳定的稳定的床面,即表层泥沙趋向于起动,“次表层”泥沙处于稳定状态(瞬时意义)。
(2)对于散体非均匀沙来讲,大部分表层泥沙颗粒的隐蔽度都不大于0.5。当某个颗粒的隐蔽度趋近于零时,则称该颗粒处于“完全暴露”状态(见图5(a))。而对于极个别的表层沙颗粒来讲,颗粒隐蔽度也有可能大于0.5,此时水流升力(脉动上举力)起主要作用,该泥沙仍可以跳跃起动,则称该颗粒处于“伪完全隐蔽”状态(见图5(b))。由于泥沙颗粒以这种起动(非输移)形式的概率很小(约占3%)[4],在研究泥沙颗粒隐蔽度时,往往忽略瞬时“伪完全隐蔽”状态的影响。当上游颗粒在所研究颗粒起动之前“下落”(包括沉落、滑落和滚落)到该颗粒上游的“空隙”处(见图5(b))时,该颗粒则会因为被上下游2个颗粒“卡住”而不能瞬时起动,则称该颗粒处于“完全隐蔽”状态(见图5(c))。由于此状态下“粒间作用力”不能忽略,所建立的平衡方程(2)不成立。为修正该方程,在此给出2个假定:其一,由于水流推力力矩作用不大,我们约定此时所研究颗粒隐蔽度趋于1(暴露度长度趋于零,则水流推力力臂近似为零);其二,把“粒间作用力”N一部分与水流升力(脉动上举力)抵消,也即方程(2)中的上举力系数趋近于零,另一部分附加到颗粒自身水下重力上,用颗粒体积系数α′修正。由于“粒间作用力”N大大增加了泥沙颗粒起动的阻力矩,使得该颗粒成为真正的不能瞬时起动的“次表层”泥沙。事实上,王兴奎[4](1993)通过对颗粒临界起动脉动分析,提出脉动上举力不仅要大于颗粒水下重力,还要持续一段时间ΔT,泥沙颗粒才能起动。由于“空隙”的存在,假定上游颗粒趋向于会在Δt时间内“下落”(包括沉落、滑落和滚落)“空隙”处,泥沙颗粒隐蔽度在大于0.5时是否仍能起动,取决于Δt与ΔT的大小关系:若上游颗粒“下落”时间Δt小于水流脉动上举力持续时间ΔT,该颗粒在起动前会被上下游2个颗粒“卡住”,即该颗粒处于“完全隐蔽”状态;否则当“下落”时间Δt大于水流脉动上举力持续时间ΔT时,这说明在上游颗粒“下落”之前,该颗粒早已被水流脉动上举力扬起向下游运动。
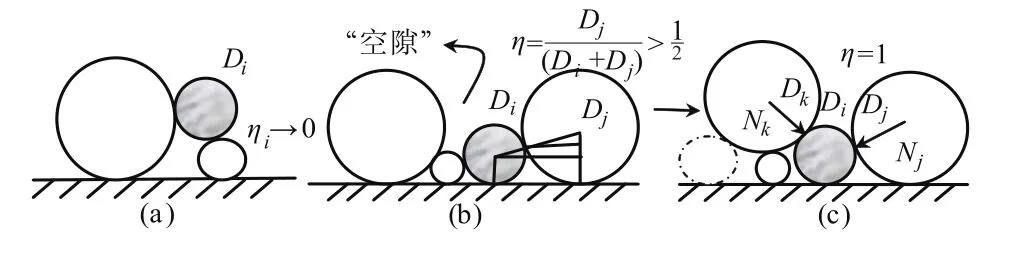
图5 非均匀沙颗粒的3种特殊状态示意图Fig.5 Three special states of non-uniform sediment particles
(3)对于散体均匀沙来讲,由于颗粒间一般不会形成足够大的“空隙”,无论是在理论意义还是现实意义上,床面表层泥沙的隐蔽度都不会大于0.5,也就是说:均匀沙颗粒理论上不存在处于“伪完全隐蔽”状态,其主要以滚动起动形式为主,泥沙起动平衡方程(2)完全适合床面表层的任何散体均匀沙颗粒。从动态角度上讲,某些均匀沙颗粒可以存在处于“完全暴露”状态(发生碰撞或翻越下游颗粒时)。
4.1 极限分析
本文已经推求出了泥沙近底作用起动流速公式(考虑函数的连续性,去掉了下标i):
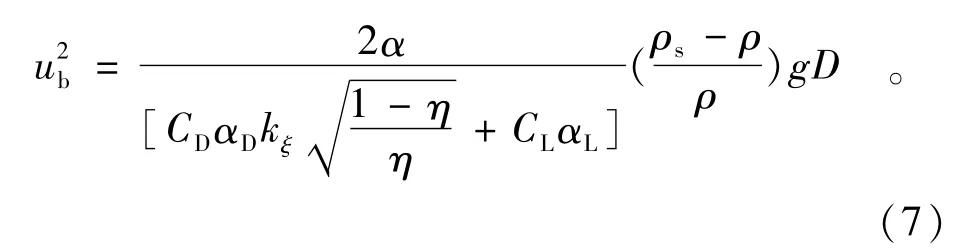
式中,CD,CL,αD,αL,α,kξ为对应的一些常数。
下面分3种情况对式(7)进行极限分析。
4.1.1 “完全暴露”
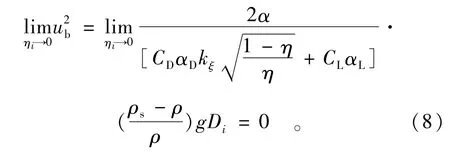
如图6所示,由于此时所研究颗粒的隐蔽度趋于零,不难计算出这说明当某个颗粒处于“完全暴露”状态时,微小的流速的水流都可以使该泥沙颗粒起动。也就是说:泥沙输移初始阶段之前,极个别“完全暴露”泥沙颗粒会通过微动滚落到“低凹”处(具有一定的隐蔽度)来自动组织成较稳定的床面。这表明把泥沙颗粒的“极个别动”作为泥沙起动标准并不合适。
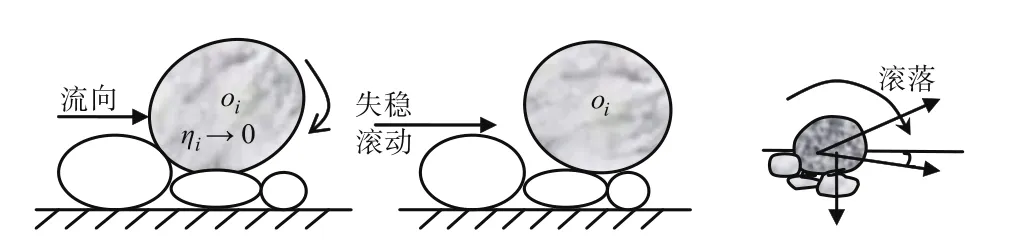
图6 泥沙颗粒“完全暴露”状态示意图Fig.6 “Com pletely exposed”state of sediment particles
4.1.2 “极限跳跃”
以“伪完全隐蔽”状态的极端“极限跳跃”为例(完全不考虑水流推力力矩的作用),如图7所示,个别表层泥沙颗粒的隐蔽度趋近1时,水流推力不能有效地促使该颗粒向下游转动,但是由于上游颗粒并不能给予该颗粒有效的“压力”,水流升力(脉动上举力)仍能促使该颗粒以跳跃方式起动[4],此时上举力系数为某一常数。若把隐蔽度趋于1代入式(7)可以得到
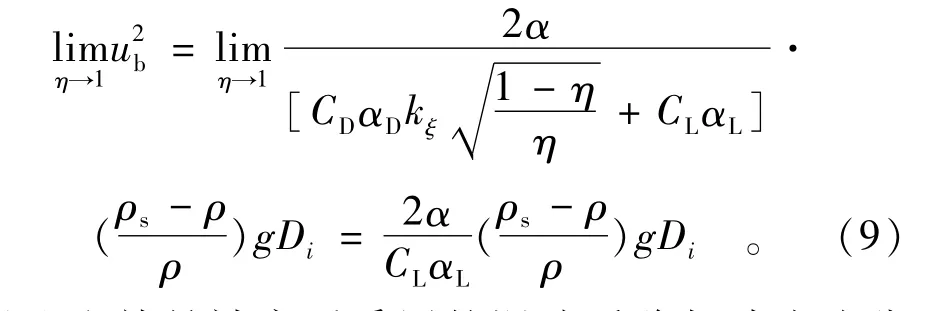
式(9)也就是被广泛采用的泥沙跃移起动流速公式。可以发现:该式的适用范围是处于“伪完全隐蔽”状态的泥沙颗粒(忽略了水流推力作用的极端情况),并且式(9)的跃移起动流速较之式(7)的滚动起动流速为大。事实上,这与Choi(2000)的试验结论[4](滚动起动的拖拽力最小,跳跃起动的拖拽力最大)也是一致的。但是泥沙颗粒以这种形式起动的概率很小(充分紊流区,约占3%)[4]。
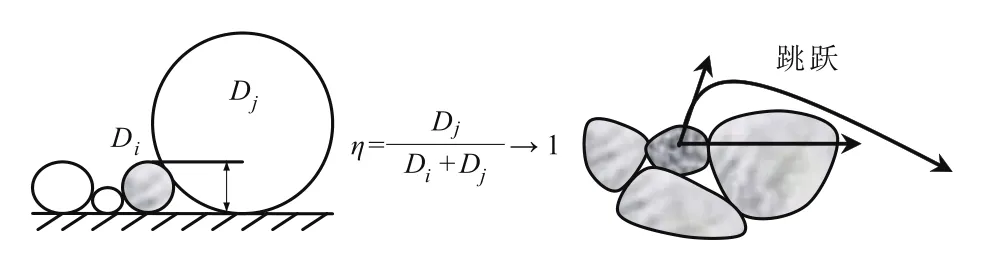
图7 泥沙颗粒“伪完全隐蔽”状态示意图Fig.7 “Pseudo com p letely hidden”state of sediment particles
4.1.3 “完全隐蔽”
如图8所示(η=1),受“粒间作用力”N的影响,认为上举力系数CL趋近与零。把此时的隐蔽度和上举力系数代入式(7)得到
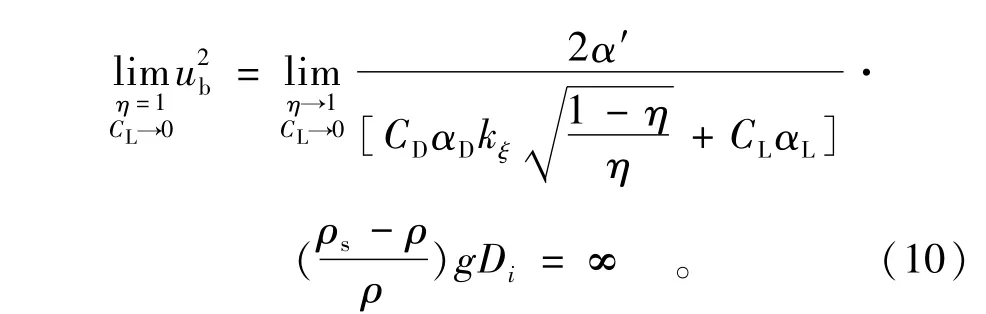
这说明“次表层”泥沙颗粒不会起动(除非在某一时刻能成为表层泥沙颗粒)。参考M.S.Yalin的观点(在相邻颗粒没有他移以前,该颗粒不可能进入运动状态[1]),可认为“完全隐蔽”的泥沙颗粒处于“自锁”状态。
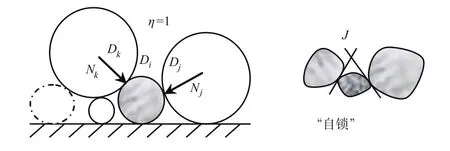
图8 泥沙颗粒“完全隐蔽”状态示意图Fig.8 “Completely hidden”state of sediment particles
综上所述,我们可以得到一个论点:所研究泥沙颗粒在不同时间不同地点的隐蔽度变化可以直接影响该泥沙颗粒的运动状态,这也就能很好地解释床面上某些颗粒在不同情况下为何出现“容易移动”、“难以起动”和“走走停停”的现象。
4.2 单调性分析
根据泥沙起动流速的物理意义,可以认为u2b是一个关于隐蔽度的单值函数,对η求导数后得
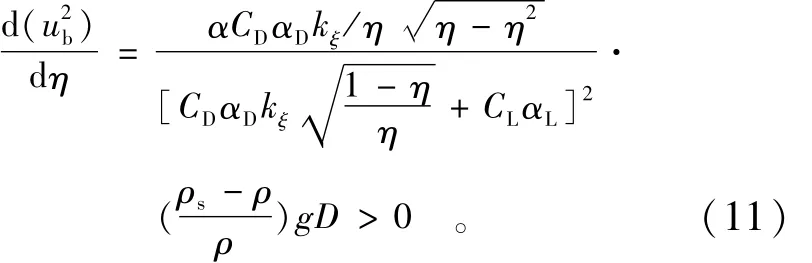
5 散体均匀沙起动切应力
褚君达对国内外散体均匀沙起动条件的研究进行了汇总,为了方便与其他学者的研究成果进行比较,他取近底流速的特征高度为泥沙颗粒粒径,即认为近底作用流速与摩阻流速的转化关系为[5]ub=8.5u*。若把该式代入式(7)可得
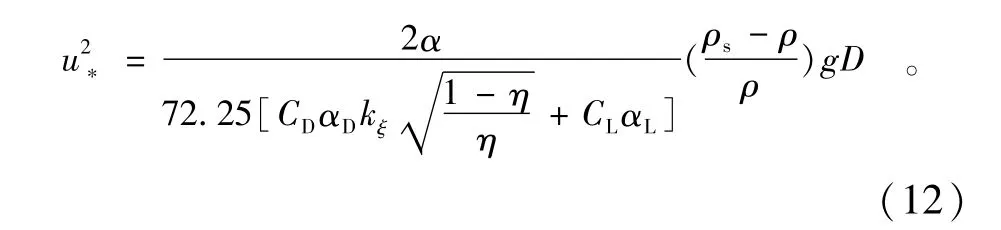
把CD=0.4,CL=0.1,kξ=0.53,αD=π/4,α=π/6代入式(12)得起动切应力为
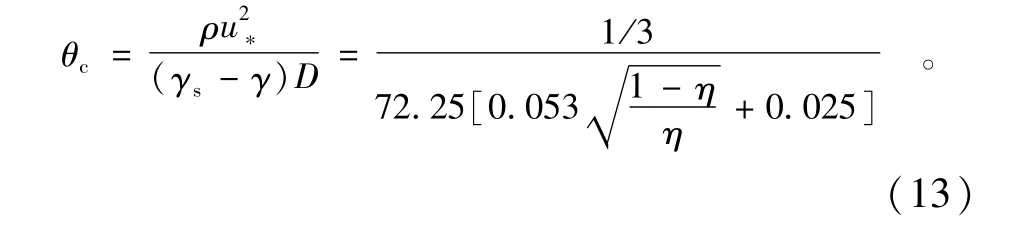
文献[3]已分析出均匀沙隐蔽度的取值区间为[0.067,0.5]。对于床面上的散体沙来讲,总有某些颗粒的隐蔽度很小,略大于0.067;也总存在某些颗粒的隐蔽度很大,略小于0.5;也有一些颗粒隐蔽度介于期望0.283 5左右。把泥沙颗粒隐蔽度从0.067到0.5变化代入式(13),可以得到无因次起动切应力(shields数),即
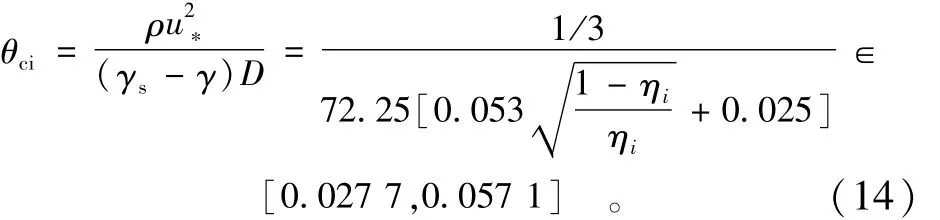
这也说明:对于泥沙颗粒隐蔽度不同的取值,可以得到对应的泥沙起动条件。该区间基本涵盖了褚君达对众多学者的统计值[5],与钱宁的统计区间[0.03~0.06]也是一致的[1]。由于泥沙颗粒在不同的情况下完全有可能呈现出不同的隐蔽度,也就对应不同的起动条件,因此众多学者的研究成果都具有一定的合理性。
另外,根据克雷默(H.Kramer)对泥沙起动的判别标准[6]:①弱动—床面上这里或那里有屈指可数的细颗粒处于运动状态;②中动—床面上有中等大小颗粒在运动,运动强度已无法计数;③普动—各种大小的颗粒已投入运动,并持续地普及床面各处。
床面上表层泥沙在冲刷前都被各自的“次表层”泥沙“支撑”,表层颗粒间互不影响,此时表层颗粒的隐蔽度较小,甚至某些颗粒的隐蔽度较小,很容易在较小水流作用下起动;随着水流强度的增大,表层泥沙颗粒会发生相互挤压与碰撞,颗粒自动组织成相对稳定的床面,此时颗粒的隐蔽度则相应增大,对应的颗粒难变得以起动。笔者认为:
(1)当表层颗粒排列非常疏松时(冲刷前),η可取0.067,此时θc=0.020 7,该值可以认为是泥沙“弱动”标准下的起动条件。
(2)当表层颗粒排列比较紧密时(冲刷中),η可取0.283 5,此时θc=0.042 2,该值可以认为是泥沙“中动”标准下的起动条件。
(3)当表层颗粒排列非常密实时(粗化层),η可取0.500,此时θc=0.059 1,该值可以认为是泥沙“普动”标准下的起动条件。
另外,对于非均匀沙来讲,式(13)同样适合研究散体非均匀沙起动。在研究分级起动时,大颗粒的隐蔽度较小,小颗粒的隐蔽度较大,中等颗粒隐蔽度居中,至于某一级配粒径颗粒的起动条件,这还取决于该级配泥沙颗粒在整体床沙中所占的比重[3]。
6 结语与展望
(1)在前人研究的基础上,从理论上建立了以隐蔽度(或“暴隐比”)为参数的散体起动流速的理论公式。通过对该式分别进行的极限分析和单调性分析,不仅论述了泥沙颗粒起动的几个特殊现象,也从数学上论证了宽级配非均匀沙的起动特性。
(2)分析起动标准及相对隐蔽度分布特性,建立散体沙起动临界切应力与相对隐蔽度在不同起动标准下的数值关系。同时也从泥沙颗粒相对隐蔽度的角度阐述了人们对泥沙起动条件认识不一的原因。
(3)两个半世纪以来,国内外学者取得大量卓越的泥沙起动流速研究成果,但是仍存在一些微观问题需要我们探索。例如,CD,αD,CL,αL,α,m等系数的准确取值,近底流速特征高度的准确取值,悬移质含沙量对推移质泥沙颗粒起动流速的影响,泥沙起动标准不统一等。
[1] 钱 宁,万兆惠.泥沙运动力学[M].北京:科学出版社,1983:229-233.(QIAN Ning,WAN Zhao-hui.Dynamics of Sediment Movement[M].Beijing:Science Press,1983:229-233.(in Chinese))
[2] 韩其为,何明民.非均匀沙起动机理及起动流速[J].长江科学院院报,1996,13(3):12-17.(HAN Qi-wei,HEMing-min.IncipientMechanism and Incipient Velocity of Non-uniform Sediment[J].Journal of Yangtze River Scientific Research Institute,1996,13(3):12-17.(in Chinese))
[3] 孟 震,杨文俊.基于二维泥沙颗粒的相对隐蔽度初步研究[J].长江科学院院报,2011,(5):1-4.(MENG Zhen,YANG Wen-jun.Preliminary Research on 2-D Hidden Degree of Sediment Particles[J].Journal of Yangtze River Scientific Research Institute,2011,(5):1-4.(in Chinese))
[4] 王兴奎,邵学军,李丹勋.河流动力学基础[M].北京:清华大学出版社,2002:209-210.(WANG Xing-kui,SHAO Xue-jun,LIDan-xun.Fundamentals of River Dynamics[M].Beijing:Tsinghua University Press,2002:209-210.(in Chinese))
[5] 褚君达.无粘性泥沙的起动条件[J].水科学进展,1993,4(1):37-43.(CHU Jun-da.Conditions of Incipient Motion of Non-cohesive Sediments[J].Advances in Water Science,1993,4(1):37-43.(in Chinese))
[6] 张瑞谨.河流泥沙动力学[M].北京:中国水利水电出版社,1998:63-84.(ZHANG Rui-jin.River Sediment Dynamics[M].Beijing:ChinaWater Power Press,1998:63-84.(in Chinese) )
(编辑:周晓雁)
Hidden Degree Applied in the Research on Incipient M otion of Cohesionless Sediment Particles
MENG Zhen,YANGWen-jun
(Key Laboratory of Management of Rivers and Lakes&Flood Control of Ministry ofWater Resources,Yangtze River Scientific Research Institute,Wuhan 430010,China)
Based on the results of sediment hidden degree research,an incipient velocity formula with hidden degree as its parameter was deduced in this paper using the rollingmodel of sediment incipientmotion.The formula was applied in limit analysis and monotonicity analysis to theoretically expound the physical phenomena of incipient motion and to demonstrate the starting characteristic of broadly graded non-uniform cohesionless sediment.The numerical relations between hidden degree and non-dimensional incipient shear stresswere established via the analysis on incipientmotion criterion and the characteristic of hidden degree distribution of cohesionless sediment particles.Finally,former research achievements are taken tomanifest the applicability of this incipient velocity formula.
hidden degree;incipientmotion;limit;monotonicity;incipientmotion conditions
TV142
A
1001-5485(2011)07-0001-06
2010-11-01
国家重点基础研究发展计划(973计划)资助课题(2007CB7141O6);国家自然科学基金资助项目(51079008);湖北省自然科学基金(2010CDB00201)
孟 震(1985-),男,河南商丘人,硕士,从事水力学及河流动力学研究,(电话)13628676681(电子信箱)edison9981@gmail.com。

