网络编码机会协同中继中断概率分析

梁文文， 田 华， 徐友云， 许 魁

（解放军理工大学 通信工程学院，江苏 南京 210007）

0 引言

网络编码[1]概念最初产生于有线网络，采用网络编码技术可以有效的提高网络吞吐量、资源利用率和均衡网络负载等。物理层网络编码[2]将信息传输降低到2个时隙，进一步提高了网络吞吐量。文献[3]提出了一种自适应网络编码协作方案。

双向多中继系统中采用网络编码可以很好的提升网络性能，在采用最大比合并(MRC, Maximal Ratio Combining)时虽然系统中断性能较好但复杂度高。采用机会中继[4-6]可以很好的降低系统复杂度并且可以达到和空时编码相同的分集复用均衡。文献[6]给出了主动式和被动式的2种中继选择策略，不但降低了系统复杂度，并且得到了较好的系统中断性能。

根据文献[6]所给的主动式中继选择略，分析了译码转发方式下基于网络编码的双向多中继系统平均中断概率性能，给出了系统平均中断概率的精确表达式。通过Monte Carlo仿真验证了理论分析的正确性。根据仿真结果，分析了不同功率分配因子和中继节点个数时的系统中断性能，根据不同条件下的中断性能比较和分析，揭示了源节点和中继节点之间的功率分配因子与系统总功率和中继节点个数之间的内在关系，同时指出在双向多中继系统中采用机会中继时，功率分配因子取值在0.6时能够获得最优的系统中断性能。

1 系统模型

图1中S1和S2为源节点，rk为中继节点，k∈1,2，…,N。中继节点采用文献[6]中的译码转发方式，整个传输过程分为3个时隙：时隙1，源节点S1以功率P1向所有中继节点广播信息，能够对S1广播的信息进行正确译码的中继节点构成了一个中继节点集合RNC1；时隙 2，源节点S2以功率P2向所有中继节点广播信息，能够对S2广播的信息进行正确译码的中继节点构成了一个中继节点集合RNC2；时隙3，在可进行网络编码的中继节点集合RNC中选择最佳中继将接收到的信息进行网络编码后再广播。

假设所有信道是均值为0，方差为1的瑞利衰落信道，且满足E。假设系统总功率受限，且总功率为P，的发送功率与源节点的发送功率满足≤P。

2 网络编码中继节点集合

定义中断概率Poutage为任意2个节点之间的互信息I小于要求的频谱利用率R的概率：

源节点与中继节点之间的互信息为：

其中Pi为源节点的发送功率，No为噪声功率。由于整个传输过程需要3个等时阶段，根据文献[9]，需要对频谱效率进行平均，因此有因子1/3。

对源节点Si的信息可正确译码的中继节点集合用RNCi表示，则RNCi可定义为：

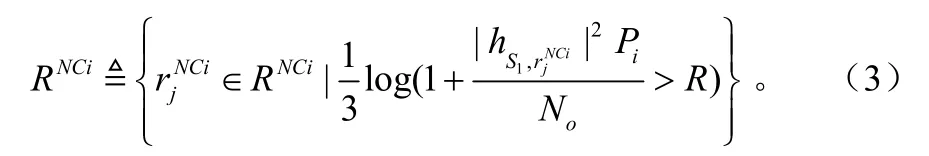
则可进行网络编码的中继节点集合为：

也就是说式（4）所表示的中继节点集合RNC中的每一个节点均满足式（3），即：

中继节点能否正确译码是相互独立的，N个中继节点构成任意一种网络编码集合的概率为：

3 系统平均中断概率

3.1 基于机会中继的条件中断概率

由于集合Wk中的每一项服从参数λ=1的指数分布，则可以得到：

由于L=0时条件中断概率为1，则以下均为L＞0的情况。最佳中继节点选定后，向S1和S2广播网络编码信息，此时，到S1的互信息为：

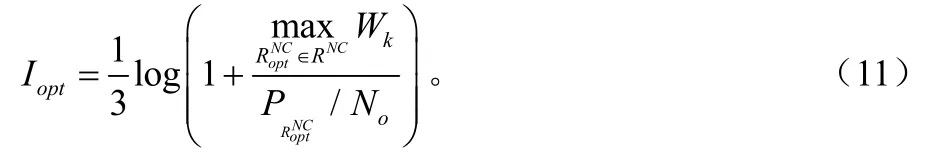
根据式（1）和式（11），条件中断概率可表示为：

3.2 系统平均中断概率

对一个中继节点个数为N的双向多中继系统，可进行网络编码的中继节点集合有2N个，考虑所有情况，整个系统

的平均中断概率表示为：

最后，将式（8）和式（13）代入式（14）中可得到系统的平均中断概率：

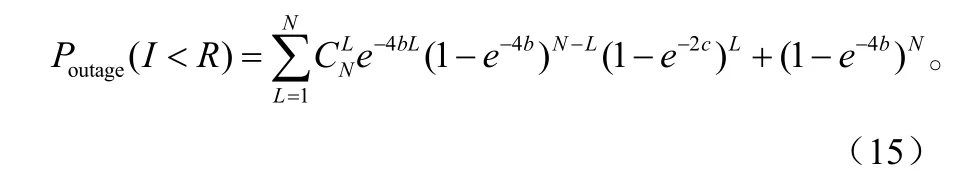
4 仿真结果和性能分析

仿真中假设所有信道是瑞利衰落信道，即信道功率增益均值为0、方差为1的复高斯随机变量，系统频带利用率R为1(bit/s/Hz)，功率分配因子α取值范围为(0,1)。

如图2所示在功率分配因子α=0.5网络中存在5、10、15和20个中继节点情况下，系统平均中断概率的理论值和Monte Carlo仿真与信噪比的关系曲线。从图2可以发现，理论值和Monte Carlo仿真吻合的很好，这充分证明了公式（15）所给的中断概率表达式的正确性。同时从图2中还可以看出，在功率分配因子确定的情况下，随着中继节点的增多，系统中断性能越好。

图2 理论值和仿真值在不同中继个数下的比较

图3所示为10个中继节点时，不同功率分配因子情况下系统平均中断概率与信噪比的关系曲线。在进行 Monte Carlo仿真和理论值计算时，功率分配因子分别取0.1、0.2、0.3、0.4和0.5。从图3中Monte Carlo仿真和理论值的比较可以看出，Monte Carlo仿真和理论计算也吻合的很好，充分证明了公式（15）的正确性。

由于图2和图3已经证明了理论分析的正确性，以下仿真结果均用理论值来表示。如图4所示，信噪比为15 dB，中继节点个数分别为5、10、15和20时系统平均中断概率和功率分配因子的关系曲线。关于功率分配问题，文献[9]采用统计搜索的方法，指出在大多数网络配置情况下，最优功率分配因子是在0.5～0.6范围内变动。本文采用机会中继，对双向多中继系统的最优功率分配情况进行了分析，可以看出，本文模型下功率分配因子在0.6时为最佳。

图5所示为中继节点个数为10，信噪比分别取20、22、24、26、28和30等情况下系统平均中断概率和功率分配因子的关系曲线。从图5可看出，功率分配因子在0.6或0.6附近时系统中断性能最佳。

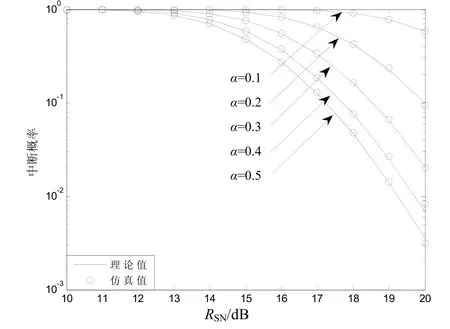
图3 理论值和仿真值在不同功率分配因子下的比较

图4 不同N时中断概率和功率分配因子的关系

图5 不同信噪比时中断概率和功率分配因子的关系

4 结语

采用机会中继，对基于网络编码的双向多中继系统平均中断概率进行了分析，给出了系统平均中断概率表达式，分析了网络中存在不同个数中继节点和不同功率分配因子时的系统中断性能，根据不同条件下的中断性能比较和分析，指出在双向多中继系统中功率分配因子取值为0.6或0.6附近时能够获得最优的系统中断性能。

[1]AHLSWEDE R, CAI N, LI S Y R, et al. Network Information Flow[J].IEEE Transactions on Information Theory,2000, 46(04):1204-1216.

[2]ZHANG S, LIEW S, LAM P. Physical Layer Network Coding[C]. In Proceedings of MobiCom 2006: 358-365.

[3]潘博，周武旸.一种新型自适应网络编码协作方案[J].通信技术,2010,43(03):102-104.

[4]范斌，王文博，林懿诚,等.译码转发中继系统中继节点选择及性能分析[J].北京邮电大学学报，2009，32(04):99-103.

[5]SONG Lingyang, HONG Guo, JIAO Bingli, et al. Joint Relay Selection and Analog Network Coding Using Differential Modulation in Two-Way Relay Channels[J]. IEEE Transactions on Vehicular Technology, 2010, 59(06): 2932-2939.

[6]AGGELOS Bletsas, HYUNDONG Shin, MOE Z W. Outage-Optimal Cooperative Communications with Regenerative Relays[J]. IEEE Transactions on Information Theory,2006,38(1):632-637.

[7]LANEMAN J N, WORNDL GW. Distributed Space-time Coded Protocols for Exploiting Cooperative Diversity in Wireless Networks[J].IEEE Transactions on Information Theory,2003,49(10):2415-2425.

[8]BLETSAS A, SHIN Hyundong, WIN M Z. Cooperative Communications with Outage-optimal Opportunistic Relaying[J].IEEE Transactions on Wireless Communication,2007,6(09)：3450-3460.

[9]LUO Jianghong, BLUM R S, CIMINI L J.et a1. Decode and Forward Cooperative Diversity with Power Allocation in Wireless Networks[J]. IEEE Transactions on Wireless Communications,2007,6(03)：793-799.