界面特性及骨料分布对混凝土破坏模式影响

黄景琦，金 浏，杜修力

（北京工业大学 城市与工程安全减灾教育部重点实验室，北京100124）

在细观水平上，混凝土可看作由骨料、砂浆、界面等组成的多相复合材料。混凝土细观力学研究的核心目标是如何建立混凝土宏观性能与其细观组分性能的关系。过渡区界面（ITZ）是混凝土细观组分中的相对薄弱环节，混凝土的破坏首先从界面处产生继而向其它组分中扩展，对混凝土的宏观力学性能及破坏过程有着巨大的影响；同时，混凝土内部骨料之间的复杂的应力场也会在很大程度上影响混凝土的力学性能。

对于界面过渡区（ITZ）的研究一直是混凝土细观力学研究的难点。Lybuimove[1]首先从细观层次研究混凝土，提出了过渡区界面（ITZ）的概念，认为ITZ是混凝土的薄弱区域。与基体相比，过渡区界面具有低强度、低弹性模量和高渗透性的特点，从而导致混凝土的力学性能在很大程度上受界面过渡区性能的影响[2]。Lee等[3]基于数值积分的方法建立了考虑物质不连续性的混凝土三相细观结构模型，研究了ITZ的弹性模量和体积对混凝土宏观弹性模量的影响；郑建军等[4]将不均匀界面层划分成一系列同心球壳单元，通过反演方法确定了每个球壳单元和水泥石基体的弹性模量，提出了考虑不均匀界面时混凝土弹性模量预测的解析法；Bentur等[5]认为ITZ结构及其性能变化对混凝土强度的影响通常在20%～30%范围内；Prokopski等[6]通过采用或不采用石蜡对白云石集料以及卵石集料进行表面处理，研究了ITZ对混凝土抗压强度的影响，结果发现：对集料进行表面处理可使混凝土的抗压强度降低50%以上。在数值模拟方面，于庆磊等[7]采用数字图像的处理手段获取混凝土界面过渡区的形状与分布，模拟了界面强度对混凝土拉伸破坏的影响；杜修力等[8]对全级配细观混凝土梁的弯拉实验进行了数值模拟，研究了界面性能对混凝土弯拉梁承载力的影响。

骨料性能对混凝土宏观性能具有很大影响。在细观数值模拟方面，马怀发等[9－10]研究了凸型骨料的生成方法，对比了骨料形状不同对混凝土性能的影响，得出凸型骨料更能反映真实情况的结论；琚宏昌等[11]研究了骨料形状的不同对混凝土宏观拉伸力学性能的影响，得出圆形骨料试件下降段平缓而多边形骨料试件脆性较强的结论。目前，对骨料空间分布形态所带来的影响研究较少。实际上，混凝土在外荷载作用下，内部骨料间会产生复杂应力场，骨料分布的改变会使得应力场也发生改变，从而混凝土的裂纹扩展形态也可能会发生很大改变。

文章将混凝土看作由骨料、砂浆和界面组成的三相复合材料，建立随机骨料模型，使用扩展有限元法（XFEM）对模型进行单轴拉伸及弯拉破坏模拟，研究界面特性及骨料空间分布形式对混凝土宏观力学性能及破坏模式的影响。

1 扩展有限元基本原理

扩展有限元方法是在传统有限元方法框架内基于单位分解法及水平集理论而提出的模拟裂纹在材料体内扩展过程的新型数值模拟方法[12]。单位分解法保证了扩展有限元方法的收敛性，水平集理论确定裂纹位置、追踪裂纹发展。扩展有限元继承了传统有限元方法的优点同时又具有传统有限元无法比拟的优势。

1.1 单元非连续位移场的建立

图1是含有一条裂纹的有限元网格，在裂纹面和裂纹尖端附近的位移逼近函数相比常规有限元要有所增强，具体来说，裂纹面所影响的单元的位移逼近函数须包含不连续的Heaviside函数（阶跃函数）；而对于裂纹尖端的单元，裂尖函数必须能体现出渐进裂尖位移场的径向和环向的性态。单元位移的逼近函数可以表示成如下形式[13]：

其中，I是此单元所有节点的集合，（ui，vi）是节点i的常规自由度，φi是与节点i相关的形函数，J是裂纹面（即被裂纹完全穿过，但不包含裂纹尖端）单元的节点集（如图1中的实心方块所示），函数 H（x）是 Heaviside函数，（b1j，b2j）是相应的额外加强自由度，φj为j节点域的形函数。Mk是裂尖k周围需要改进的节点集合（如图1中的空心圆点所示），（a（tipk）1m，a（tipk）2m）为裂尖处与弹性渐近裂尖函数有关的节点加强自由度，φm为裂尖单元的形函数。

图1 含有裂纹的网格

若一个结点同时属于裂尖单元和被裂纹分割单元时，则优先属于裂尖单元。式（1）表明：若单元中没有裂纹经过，则该单元的位移场为等式右边第一项；若单元被裂纹完全贯穿，则该单元的位移场为等式右边前两项；若单元是裂尖所在单元，则该单元的位移场为右边第一项和第三项的和。

采用广义Heaviside函数，其取值规则为在裂纹上方H（x）取1，在裂纹下方H（x）取－1来反映位移的不连续情况，在局部坐标系（图2所示）内表达为：

图2 裂尖处局部极坐标系

其中，x是所考察的点，x＊是离x最近的裂纹面上的点，且n是x＊处裂纹的单位外法向矢量。

对于各向同性的弹性体，裂纹尖端附加的改进函数为[14]：

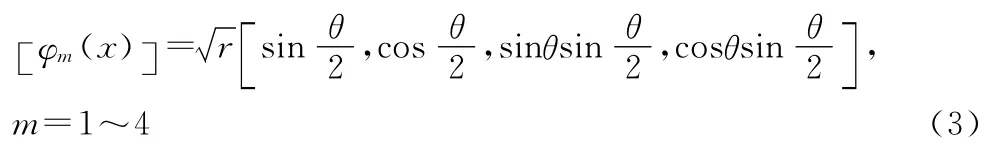
其中，r和θ为局部裂尖场坐标系统中的极坐标。

1.2 断裂准则及裂纹扩展方向确定

开裂准则[15]采用最大拉应力准则，在平面应变状态下，最大拉应力为：

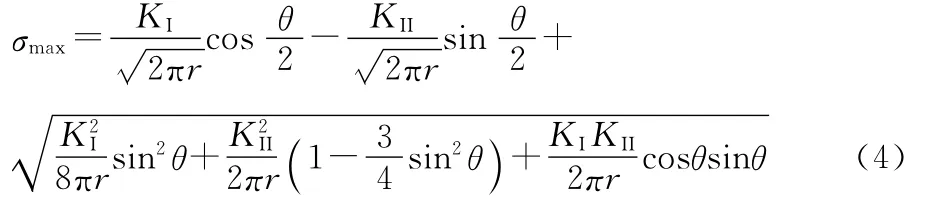
式中，KI、KII为I型、II型裂纹的应力强度因子。简单的说，认为σmax达到允许应力σt时，裂纹失稳扩展。

裂纹沿着垂直于最大拉应力方向开展，开裂角θc为：

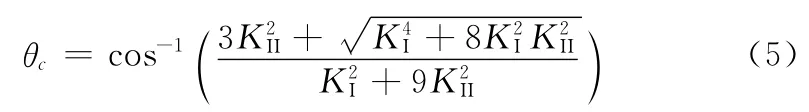
式中，θc的方向为前段裂纹延伸线逆时针方向量起。

2 混凝土细观随机骨料模型建立

从细观层次上考虑，混凝土材料可被认为是由骨料、砂浆基质及两者间过渡区界面组成的三相复合材料。首先建立二级配混凝土的随机骨料模型，如图3所示，平面尺寸为150mm×150mm，骨料颗粒（图3中“红色区域”）周围2mm厚度薄层区域被设定为界面过渡区（ITZ），即图4中“黄色区域”；“蓝色区域”代表砂浆基质。

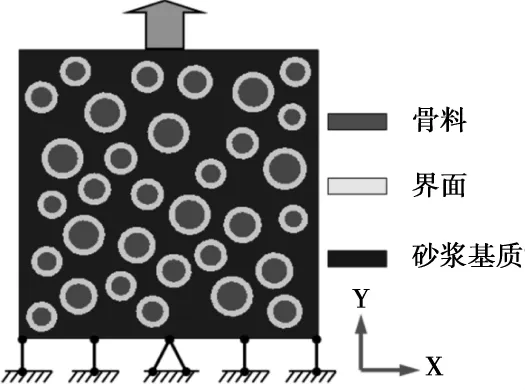
图3 混凝土细观随机骨料分析模型

混凝土细观各相材料采用如图4所示的本构关系曲线，即认为：细观组分（骨料、砂浆和界面相）在达到各自的峰值应力前，应力－应变关系是线弹性的；当达到峰值应力后，采用线性应力－裂缝宽度关系来表征混凝土材料的软化力学行为。其中，ft为混凝土细观材料的极限拉伸强度；Gf为断裂能；W 为张开位移，WS为极限张开位移。各细观组分的力学参数见表1。采用位移加载控制，将最大拉应力准则作为材料开裂准则。

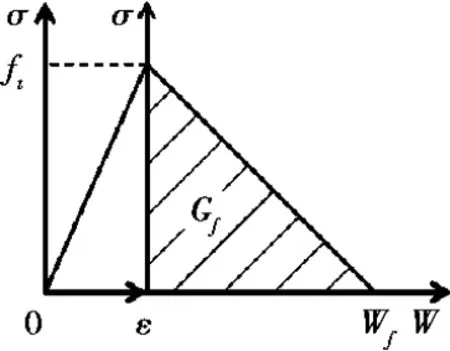
图4 混凝土细观组分本构行为

表1 混凝土各组分力学性质

3 界面强度对混凝土破坏机理影响

3.1 混凝土细观拉伸破坏过程模拟

单轴拉伸条件下二级配混凝土试件的断裂破坏过程如图5所示。由于篇幅所限，本文只给出了界面抗拉强度为2.0MPa的裂纹扩展过程。从图5中可以看出，在外荷载作用下，混凝土试件首先在内部薄弱区域（即界面区）达到其抗拉强度，产生断裂破坏，随着外荷载增大，内部裂纹向砂浆基质中扩展延伸。由于裂纹在试件中扩展演化，使得混凝土试件整体刚度下降，最终内部宏观裂纹产生直至贯穿整个试件。

图5 单轴拉伸条件下混凝土断裂破坏过程

3.2 不同界面强度的混凝土细观破坏模式对比

界面是混凝土材料的相对薄弱部位，与砂浆基质相比，具有低弹模、低强度的特点。本文对不同界面强度（1.5MPa、2.0MPa、2.5MPa、3.37MPa）下的混凝土试件进行单轴拉伸模拟对比研究。

图6 不同界面强度下混凝土破坏模式对比

图6给出了不同界面强度所对应的破坏形式，显然，界面强度对混凝土破坏模式具有较大影响，混凝土起裂位置、扩展的方向路径都有很大的不同。

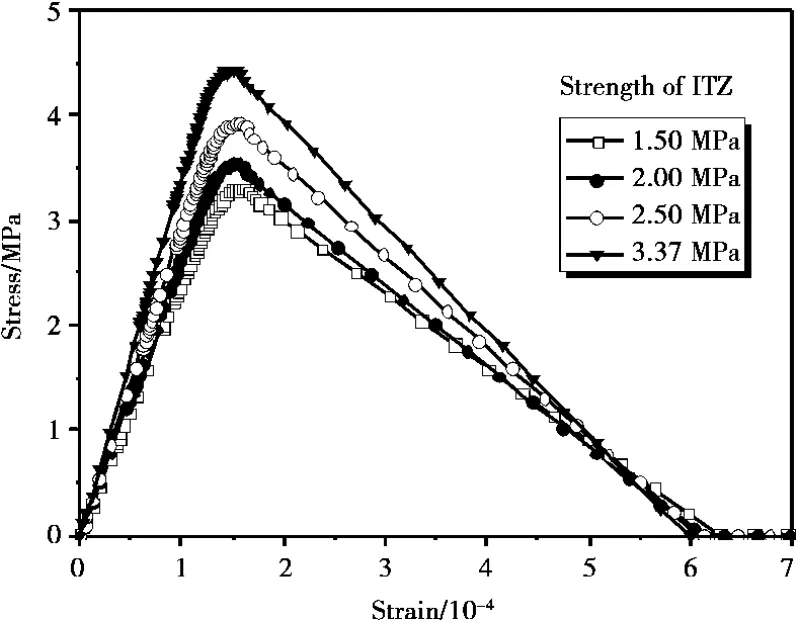
图7 不同界面强度的混凝土宏观应力－应变曲线

图7给出了界面强度分别为1.50MPa、2.00MPa、2.50MPa、3.37MPa的混凝土单轴拉伸应力－应变曲线。可以看出，界面强度影响着混凝土的极限抗拉强度，随着界面强度提高极限抗拉强度也在增高，达到强度后的下降段曲线明显不同，也正说明界面区影响着混凝土材料的破坏路径；当界面强度达到3.37MPa时，界面材料与砂浆材料相同，混凝土的破坏模式和应力－应变曲线与其它界面强度相比具有明显不同，表明考虑界面相存在是非常有必要的。

3.3 不同界面强度的混凝土弯拉梁破坏模式

建立几何尺寸为450mm×150mm的混凝土四分点弯拉梁模型，如图8，两边为混凝土弹性区，混凝土弹模为35 GPa、泊松比为0.20，中间为150mm×150mm的细观剖分区，各组分材料力学参数取值同表1，采用位移加载控制。

图8 混凝土细观弯拉梁模型

对不同界面强度下的弯拉梁进行加载模拟，得到了不同界面强度下梁的破坏模式（图9）和荷载－位移曲线（图10）。从图9、图10中看出，界面强度影响着梁的力学性能及破坏模式。不同界面强度的混凝土梁具有明显不同的破坏形式；界面强度越高混凝土梁承载力越高。

图9 不同界面强度下混凝土弯拉梁破坏模式对比

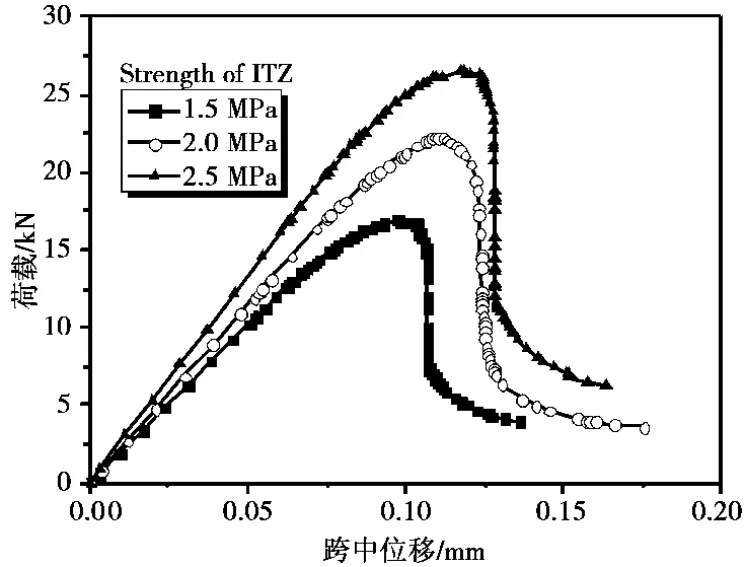
图10 不同界面强度下混凝土弯拉梁荷载－位移曲线

4 骨料分布对混凝土破坏机理的影响

混凝土在外荷载作用下，内部骨料间会产生复杂应力场，骨料分布的改变会使得应力场也发生改变。本文建立两种不同骨料空间分布的随机骨料模型，如图11所示，对其进行单轴拉伸破坏模拟，研究骨料空间分布对混凝土的影响。

图11 两种不同随机骨料模型

图12 不同随机骨料模型的破坏模式对比

图13 不同随机骨料模型的应力－应变曲线

数值模拟的结果表明：不同骨料分布的混凝土具有截然不同的破坏路径，如图12，表明骨料的空间分布会对混凝土的破坏模式产生影响；在图13的应力－应变关系中，峰值前的曲线段基本相同，表明骨料空间分布对混凝土弹模及强度影响基本可忽略，达到峰值后的下降段出现明显不同，说明了骨料分布不同影响着混凝土的破坏过程。

5 结 论

通过对不同界面强度和不同骨料分布的混凝土细观模型进行加载数值模拟，分析了界面强度及骨料分布不同对混凝土力学特性及破坏模式影响，可以得到以下结论：

1）界面的存在影响混凝土的破坏模式及宏观力学性能，在对混凝土破坏机理及力学性能进行研究时必须考虑界面的影响；

2）骨料空间分布形式基本不影响混凝土宏观弹模及强度，但对混凝土的细观破坏路径有很大影响。

[1]LYBIMOVE C T Y，PINNS E R.Crystallization structure in concrete contact zone between aggregate and cement in concrete[J].Colloid Journal，1962，（24）：491－498.

[2]王 瑶，周继凯，沈德建，等.混凝土中骨料－浆体界面过渡区的力学性能研究综述[J].水利科学进展，2008，28（2）：89－94.

[3]LEE K M，PARK J H.A numerical model for elastic modulus of concrete considering interfacial transition zone[J].Cement and Concrete Research，2008，38（3）：396－402.

[4]郑建军，吕建平，吴智敏.考虑不均匀界面时混凝土弹性模量预测[J].复合材料学报，2008，25（5）：141－146.

[5]BENTUR A，ALEXANDER M G.A Review of the work of the RILEM TC 159－ETC：engineering of the interfacial transition zone in cementitious composites[J].Material Structure，2000，33（226）：82－87.

[6]PROKOPSKI G，HALBINIAKJ.Interfacial transition zone in cementitious materials[J].Cem.Concr.Res，2000，30（4）：579－583.

[7]于庆磊，杨天鸿，唐春安，等.界面强度对混凝土拉伸断裂影响的数值模拟[J].建筑材料学报，2009，12（6）：643－649.

[8]田瑞俊，杜修力，彭一江.基于细观力学全级配混凝土梁弯拉试验的数值模拟[J].水利与建筑工程学报，2008，6（1）：1－3.

[9]马怀发，芈书贞，陈厚群.一种混凝土随机凸多边形骨料模型生成方法[J].中国水利水电科学研究院学报，2006，4（3）：196－201.

[10]陈厚群，马怀发，李运成.随机骨料模型形态对大坝混凝土弯拉强度的影响[J].中国水利水电科学研究院学报，2007，5（4）：241－246.

[11]宏昌，陈国荣，夏晓舟.骨料形状对混凝土拉伸强度的影响[J].河海大学学报（自然科学版），2008，36（4）：554－558.

[12]KAZUKI S，TOMOAKI U.Evaluation on reproduction of priori knowledge in XFEM [J].Finite Elements in Analysis and Design，2011，47（4）：424－433.

[13]李录贤，王铁军.扩展有限元法（XFEM）及其应用[J].力学进展，2005，35（1）：5－20.

[14]FLEMING M，CHU Y A，MORAN B，et al.Enriched element free galerkin methods for crack tip fields[J].International Journal for Numerical Methods in Engineering，1997，40：1483－1504.

[15]董伟，吴智敏，郑长良.混凝土Ⅰ－Ⅱ复合型裂纹断裂准则研究方法概述[J].力学与实践，2006，28（6）：9－14.