缓冲器输出端相位噪声模型分析

衣明坤，王 军

（西南科技大学 信息工程学院，四川 绵阳 621010）

0 引言

低相位噪声的振荡器往往都是各种高级现代电子系统的核心技术之一[1]。振荡器相位噪声的设计准则在任何通信系统中都非常重要。在射频收发器中振荡器相位噪声与信号噪声相互混合会产生一些不良影响[2]。目前，大多数的振荡器相位噪声模型的建立过程中，并没有考虑对缓冲器噪声是如何使得振荡器相位噪声的频谱发生变化。大多数的振荡器电路用输出端口的缓冲放大器来稳定负载阻抗[3]。但是以前的研究工作者认为缓冲放大器产生的噪声会随着偏移频率的增大而无限的减小，因此，都忽略了缓冲放大器产生的噪声；显然，即使该假设成立，在近偏频点处，缓冲器噪声的影响也是不容忽略的，本文是利用双端口噪声分析理论建立统一的缓冲器噪声的功率谱密度函数数学模型，将该模型嵌入到利用非线性扰动分析理论[4]建立的不含缓冲器噪声的振荡器相位噪声功率谱密度函数表达式中，从而得到含有缓冲器噪声的振荡器相位噪声模型。

1 缓冲器噪声的功率谱密度函数数学模型

近年来随着无线通信应用的射频集成电路的发展，射频电路设计人员在建立振荡器的相位噪声模型和降低相位噪声方面作了大量卓有成效的工作[5]。大多数的振荡器电路用一些二端口的缓冲放大器来稳定负载阻抗，二端口的缓冲放大器对振荡器的影响通常在文献中都不会详细的介绍[6]。同时大部分的仿真都忽略了由输出端缓冲放大器引起的噪声本底的存在，认为随着偏移频率的增大，噪声会无限的减小。目前，在大多数的振荡器相位噪声模型的建立过程中，并没有考虑对缓冲器噪声是如何使得振荡器相位噪声的频谱发生变化，从而缺乏指导缓冲器低噪声设计的方法。下面主要介绍缓冲器的功率谱密度函数数学模型的建模方法。

首先如图1所示的二端口网络是常见的噪声模型，而图2是在二端口网络的输出端载入了一个输出噪声源2nv ，而图1则是把图2中输出端的噪声源等效到输入端。

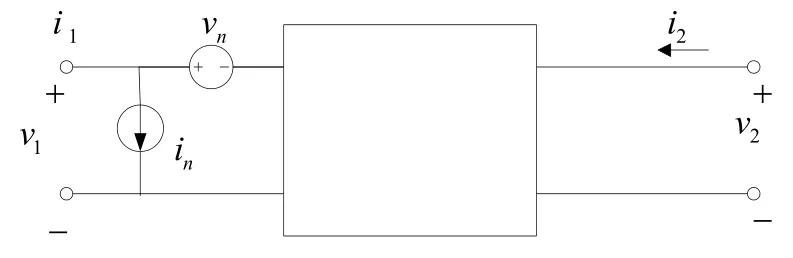
图1 常见二端口噪声网络

图2 等效二端口噪声网络

从图1和图2中，我们可以很容易的将电压 vn和电流 in通过in1和 vn2表示为：

图3展示的是含有缓冲噪声的二端口等效电路，其中输入端噪声电流和噪声电压分别为ni和nv。

图 3 含有缓冲器噪声的电路

由公式（1）和公式（2）可知由振荡器电路中的缓冲网络引入的诺顿等效噪声电流[7]为：

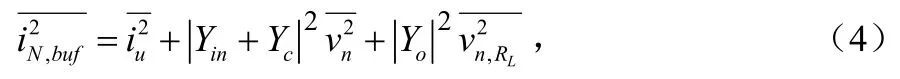
其中 Yc是相关导纳，ic= Ycvn。在这些表达式中，总的缓冲器噪声电流 in= iu+ ic，其中 iu是非相关噪声分量，ic是相关噪声分量[8]。

2 含有缓冲器噪声的振荡器相位噪声功率谱密度函数数学模型

在非线性扰动分析模型中，我们可以得到在振荡器输出端相位噪声表达式为：

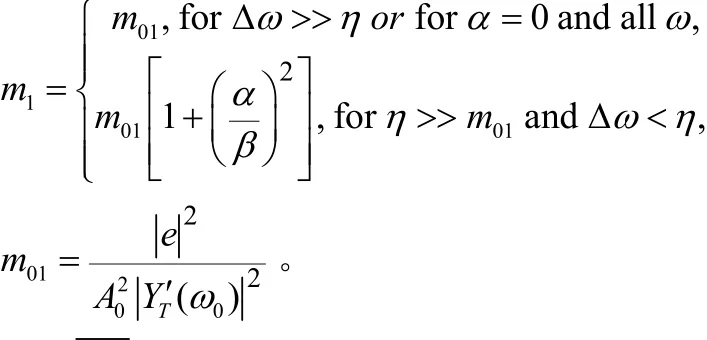
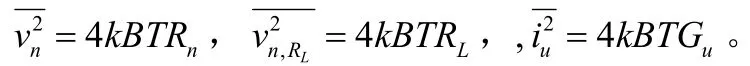
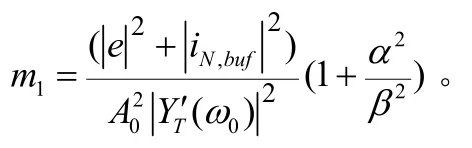
出现在输入端的等价噪声源nv直接作用在输入端的噪声本底。在缓冲放大器输出端的总的噪声（包含缓冲噪声）为：

其中vA是缓冲器提供的电压增益：vA=（即 R 得功率密度）通常是作用于

n噪声本底的主要项。在缓冲噪声本底为-130 dBV，且有2个不同白噪声 e2( 1)= 8 .5× 1 0-18A2/Hz （非常强的白噪声）e2(2) = 2 .8× 1 0-23A2/Hz （正常较弱的白噪声）的情况下噪声本底的影响可以从图4中看出。在白噪声和噪声本底之间的角频率为：

图4 缓冲器噪声对差分振荡器输出端电压功率谱密度的影响

可以注意到对于正常白噪声 e2(2)来说 f2F=η/2π，因此在白噪声频率范围内（ f ＜f2B）应该用m01代替m1。同时我们可以得到 e2(2)的模型与仿真结果之间有6 dB的偏移，其中4 dB是由于新的相关因子 (1 +cot2θ)的作用。

3 结语

本文通过对缓冲器噪声功率谱密度函数数学模型的推导，结合非线性扰动分析的特点，将此模型嵌入非线性扰动模型中，从而得到了含有缓冲器噪声的振荡器的相位噪声模型。通过仿真可以得到缓冲器噪声是如何使得振荡器相位噪声的频谱发生变化的，从而提出了指导缓冲器低噪声设计的方法，这对于研究缓冲器噪声对振荡器相位噪声影响方面具有重要意义。

[1] 胡帆，周立东.不同相位噪声谱QPSK的性能影响分析[J].通信技术，2010，43（04）:65-66,69.

[2] 周殿宇，王军.基于背靠背PN变容管的低相位噪声LCVCO研究[J].通信技术，2010，43（02）:201-203.

[3] MARK Crandall. 利用缓冲放大器改善压控振荡器设计[J]. 电子产品世界,2003(09) .

[4] 姚党毅，王军.LC振荡器相位噪声的非线性摄动分析技术[J].通信技术，2011，44（01）: 157-158,161.

[5] Roychowdhury J, Demir A, Mehrotra A. Phase Noise in Oscillators:A Unifying Theory and Numerical Methods for Characterization[J].IEEE Trans，2000，47(05):655-674．

[6] PAUL Ward，AMY Duwel. Systematic Construction of an Analytical Model Encompassing Nonlinearity[J]. IEEE Trans，2011，58(01)：195-205．

[7] 李长生，王文骐，詹福春.射频应用压控振荡器相位噪声的研究[J].通信技术，2003（12）:26-28.

[8] RAZAVI B.Analysis, Modeling and Simulation of Phase Noise in Monolithic Voltage-controlled Oscillators, in Proc. IEEE Custom Integr. Circuit Conf., 1995:323–326.