基于DSP Builder的自适应滤波器的模型搭建

孟莎莎，董会宁，董 健

（重庆邮电大学 应用物理研究所，重庆 400065）

0 引言

飞速发展的数字信号处理技术（DSP，Diginal Signal Processing）在通信、医学、图像处理、多媒体系统、便携式电子设备中得到了广泛的应用。

在过去的一段时间内，DSP处理器是DSP应用系统核心器件的唯一选择，DSP Processor主要是指目前最常用的基于CPU架构的器件，通过软件指令的方式完成DSP算法[4]。近年来DSP器件在硬件结构上不断改进，性能有了很大的提高，但是并没有摆脱传统CPU的工作模式。DSP处理器的灵活性只是表现在软件更改的容易性以及对各种算法的处理和复杂算法的实现上，而对于系统硬件本身的更改，DSP是没有任何灵活性可言的。

现代大容量、高速度的FPGA能够克服DSP处理器的诸多不足，在这些FPGA中，一般都内嵌有可配置的高速RAM、PLL、LDVS、LVTTL以及硬件乘法器等DSP模块。FPGA做为数字信号处理的新硬件平台，在并行性和速度问题上突显出独特的优势，而且其灵活的可重构特性，使用FPGA搭建DSP系统非常易于实现、易于测试及硬件升级。

Altera推出的 DSP Builder工具箱提供了一个从MATLAB/Simulink直接到FPGA硬件实现的设计接口。它极大地简化了DSP功能的硬件实现流程，并提供了系统级仿真测试功能，并且DSP Builder提供模块化的门电路，使得算法更容易实现，这样就能极大地缩短开发周期。

本文在DSP Builder软件平台上，搭建了一个以四阶滤波器模块为基础的自适应滤波器，该滤波器通过级联，可以简单地转换为8阶、12阶、16阶等的自适应滤波器，通过Simulink模拟仿真，验证了该设计的的合理性，为硬件的实现打下了基础。

1 自适应滤波算法的选取

自适应滤波器是指能够根据环境的改变，使用自适应算法来改变自身滤波器参数和结构的滤波器[3]。它一般由2部分组成：①是滤波器模块；②是滤波器系数更新模块，即自适应算法模块。对于自适应算法的选取一般从2个方面考虑：①是算法的复杂度；②是算法的收敛性。

在自适应滤波器的设计中，自适应算法的选取尤其重要，算法的选取一般从两个方面进行考虑，一个是自适应算法的复杂度，一个是算法的收敛性能[6]。

由Widrow和Hoff提出的最小均方误差（LMS）算法，因其具有结构简单、计算量小、鲁棒性强、易于实现等优点而在硬件设计中被广泛采用。该算法的计算公式描述如下：

(1) FIR滤波器运算

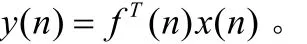
(2) 滤波器系数计算

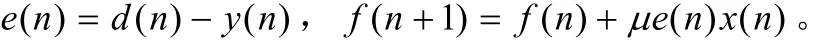
根据LMS算法的计算公式，建立一个LMS算法复杂度表，如表1，设滤波器的长度为L，那么LMS算法在一次迭代中只需要2L+1乘法和2L次加法，也就是说LMS算法的复杂度为O（L），与滤波器的阶数L呈线性增长。计算复杂度低是LMS一个显著有点，因此LMS算法在实际中得到广泛应用奠定了基础。

表 1LMS算法复杂度

自适应算法的收敛性一般由参数μ决定，LMS算法简单，只有一个参数μ，因而必须选择合适的μ，来保证算法的收敛性。另外μ还是控制收敛速度稳态误差的常量，选择大的μ可以产生很快的收敛速度，但是当收敛到维纳解附近后将在一个比较大的领域内抖动而无法进一步收敛；选择较小的步长可以收敛到维纳解附近的小领域，但是它的收敛速度是非常缓慢的。这就是LMS算法的一个明显弱点：高速收敛和小稳态误差不可兼得，而调和此矛盾的参量就是步长因子μ。为了保证算法收敛性，对步长因子的稳定边界定义如下：

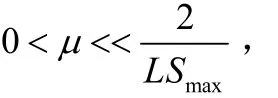
其中maxS是输入()xn的功率谱密度的最大值。

2 算法的模块划分

在本设计中，把自适应滤波器划分为几个独立的模块，这样可以保持各个模块的相对独立性，若要改变自适应算法，只需要改变算法模块即可，其它的模块可以不变，并且各个模块的恰当分割大大地增加了系统的灵活性，有利于硬件实现。

根据自适应LMS算法的计算公式，把计算分为了FIR滤波器运算和滤波器系数计算两步，相应地，把自适应滤波器的结构划分为横向FIR滤波器模块和滤波器系数更新模块，即自适应算法模块，如图1所示为给出的2个模块的结构图。因为输出误差计算模块只有一个加法运算，那么可以把这个加法运算合并到其它的2个模块进行建模。

图1 自适应滤波器的分割结构

3 基于DSP Builder的建模

DSP Builder是Altera公司推出的一个面向DSP开发的系统工具。它是作为Matlab/Simulink的一个工具箱出现的。DSP设计可以方便地利用Simulink与DSP Buider提供的丰富的功能块和IP核进行设计。DSP Buider包括比特和周期精度的 Simulink模块，还涵盖了诸如算法和存储功能基本模块以及 IP库中的许多复杂的功能模块。电路中的功能块和 IP的技术参数、数据格式和总线宽度都可以直接设置。电路模型设计完成后，可以进行系统功能仿真。仿真通过后可以运行Signal Compiler，将模型转化成RTL级的VHDL代码和Tcl脚本语言。调用QuartusⅡ进行编译，QuartusⅡ根据网表文件及设置的优化约束条件进行布线布局和优化设计的适配，最后生成编程文件和仿真文件。

通过上面的自适应滤波器结构和自适应滤波算法的分析，可知该设计有大量的乘法、加法和延迟算法，那么在Matlab的Simulink工具箱DSP Buider模块组里面，调出设计所需的乘法器、加法器、延迟单元，还有总线控制模块，完成顶层设计。用以完成算法级到功能级的实现。

鉴于以上的设计，需要对 DSP Buider中的几个模块进行说明：

①Product：乘法器；

②Parallel Adder Subtractor:加法器；

③Gain：增益模块；

④Bus Coversion:总线类型转换模块；

⑤Dalay:延迟单元。

根据模块划分思想，进行模型搭建，设计一个四阶的滤波器模块和一个四阶的滤波器系数更新模块。在实际应用中，低阶数的滤波器往往很难达到合理的滤波器效果，所以对设计的模块封装，那么再进行模块级联，就可以调整滤波器的系数，灵活地实现8阶，12阶，16阶及更多阶的自适应滤波器。如图 2所示，为一个四阶为单元组合而成的 16阶的自适应滤波器设计图，其中子模块4fir为四阶FIR滤波器模块，子模块l ms为4阶系数调整模块。通过子模块间的级联，建立一个16阶的自适应滤波器。图3为自适应算法子模块的结构图。设定时钟信号周期为 20 ns，输入信号是在正弦信号的叠加一个随机噪声信号 1，参考信号为一个和随机噪声信号1相关的噪声信号2，步长因子μ设定为0.025。开始Simulink模型仿真，其仿真结果如图4所示，第一条输出波形为正弦信号和随机噪声的叠加，第二条波形为误差号的输出，第三条波形为输出信号。

由此得出结论：

①输出信号达到了比较理想的效果；

②误差信号得到了收敛，且收敛速度较快。

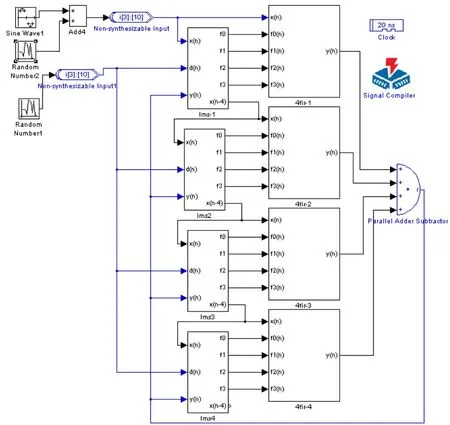
图2 16阶自适应滤波器的结构

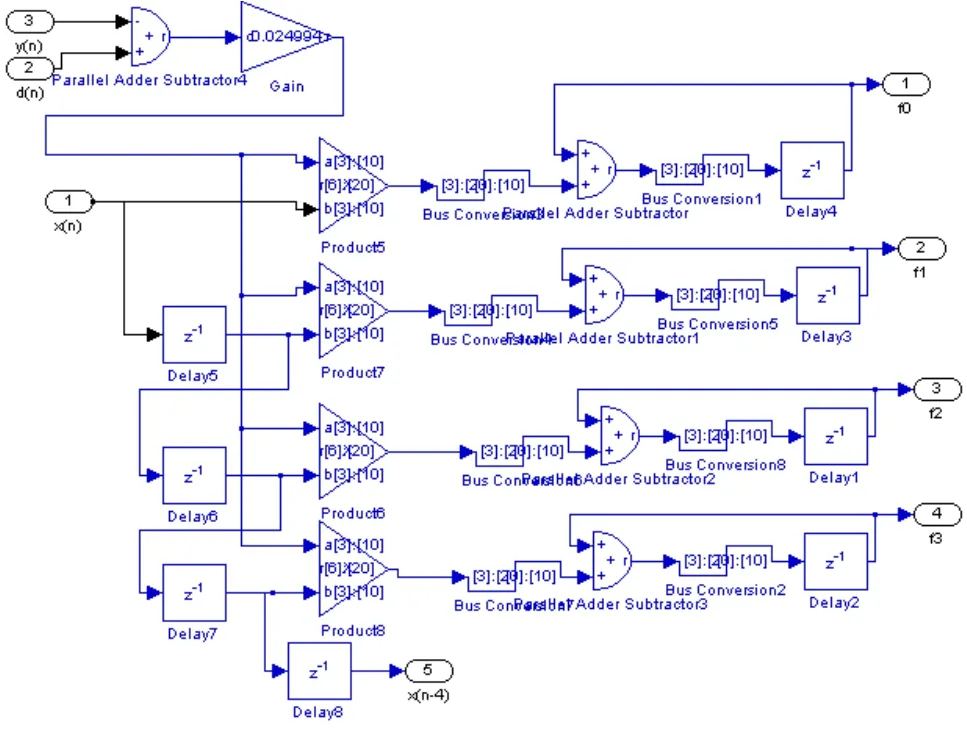
图3 系数调整模块结构

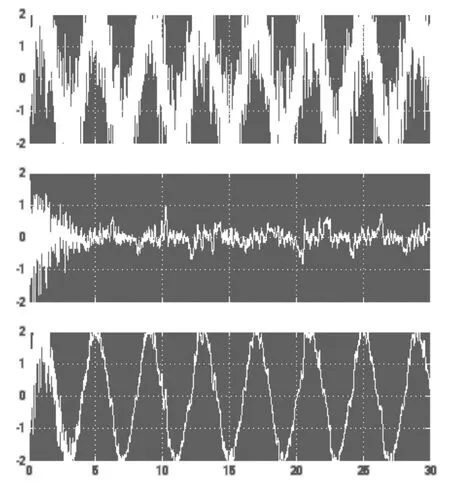
图4 自适应滤波器仿真

4 结语

本文基于DSP Builder设计软件，完成了自适应滤波器的模型搭建，这样的设计流程，包括从系统描述直至硬件实现，可以在一个完整的设计环境中完成，同时构成了一个自定而下的典型的设计流程。通过仿真，验证了设计的合理性，并且模块划分的思想使设计简单易行，极大地缩短了开发周期，并且Simulink所具有的图形界面也能帮助提高开发效率。

使用DSP Builder工具箱可以明显地提高数字信号处理系统的开发效率，并且设计者可以不必懂硬件描述语言，也能进行DSP系统的硬件开发。DSP Builder应用于数字信号处理有很高的应用价值。

[1] 李昕,李艳,李波. DLMS滤波器的 FPGA实现[J]. 元器件与应用,2009,21(09)：41-46.

[2] 张银行,杨小雪. 子带分解的自适应滤波器的 FPGA实现[J]. 现代电子技术, 2010,33（08）：13-18.

[3] 袁江南,徐敏. 基于DSPBuilder的LMS自适应滤波器设计[J]. 计算机应用 2009, 29（12）：338-340.

[4] 杨东,王建业,蔡飞. 基于DSP开发工具的自适应滤波器[J].探测与控制学报, 2010,6(08)：67-70.

[5] DAVIS B. Adaptive Noise Cancellation Using LMS and Optimal Filtering[J]. University of Florida. 2003,13(09): 23-30.

[6] 秦志强,张水莲,孙萍. 阶数可变的成形滤波器FPGA实现[J]. 通信技术,2009,42（03）：261-265.

[7] 王云，李惠光，隋明森. 模糊LMS算法主从滤波器的设计及应用[J].通信技术，2009，42（05）：74-76.

[8] 邵宁，陈万培，陈俊晟. 一种基于维纳滤波器抗MAI的新方法[J].通信技术，2010，43（05）：134-138.