某V型发动机曲轴结构强度有限元分析及方案比较

陈 伟，温世杰，彭海雄

（中国北方发动机研究所，山西大同037036）

曲轴是发动机中最重要的零件之一，承受着气缸内气体压力以及往复和旋转质量惯性力引起的周期性变化载荷。曲轴内产生交变的弯曲应力和扭转应力，可能引起曲轴的疲劳失效，甚至断裂。如何比较准确的得出曲轴应力大小以及分布，对于指导曲轴的设计和结构改进，具有很重要的意义。

本文所做的工作，是使用有限元分析法对某V型发动机曲轴的两种结构方案（简称A方案、B方案）在爆发工况载荷作用下进行应力数值模拟，对其强度计算结果进行分析，为曲轴结构设计提供理论依据。

1 三维模型的建立

曲轴各单拐的结构及所受载荷是相同的。计算模型采用3个完整的单拐，选取中间拐为爆发载荷施加位置，以中间拐为计算考察对象。按照图纸实际尺寸值，应用Pro／E软件建立曲轴结构三维实体模型如图1所示。曲轴B方案与A方案相比较，连杆轴颈增加5 mm，曲柄臂宽度增加20mm，弧度半径增加6mm。

图1 曲轴结构三维实体模型

2 有限元模型的建立

由于曲轴结构形状的复杂性、载荷的交变性，局部存在较高应力，在对曲轴进行有限元分析时，需要根据曲轴的结构特点、载荷性质以及分析目的选择适当的计算模型。

2.1 结构离散

将计算模型划分成曲轴区和支撑区两部分。各部分材料物理特性参数见表1所列［1］。

表1 各部分材料物理特性参数

为了提高有限元模型的计算精度及控制整个有限元模型的计算规模，对模型各部分设定了不同的单元长度。将主轴颈过渡圆角处、曲柄销过渡圆角处以及油孔周围网格进行细化，这样可提高这些区域的计算精度，力求准确地反映出这些区域的应力集中情况。

有限元模型曲轴实体部分，采用10节点四面体单元，轴承座因形状规则，采用六面体单元。曲轴有限元计算网格模型如图2所示。

图2 曲轴有限元计算网格模型

2.2 位移和载荷边界条件

根据曲轴的实际工作情况，在有限元模型中施加相应的位移约束边界条件和载荷边界条件。

发动机连杆受力曲线如图3所示。

按照中间拐爆发时，由曲柄连杆机构运动学计算出相邻各气缸的曲轴受力。在各拐的连杆轴颈上施加曲轴切向力和径向力。曲轴位移和载荷边界条件施加状态如图4所示。

图3 发动机连杆受力曲线

图4 曲轴位移和载荷边界条件施加状态

2.3 接触边界条件

对于由曲轴、主轴承座组成的组合结构，装配接合面上有接触关系，计算时程序根据接触状态通过接触面上建立的接触单元自动完成作用力的传递，完成接触模拟。

3 计算结果及分析

曲轴结构具体考察区域如图5所示。其中，1、6区为主轴颈过渡圆角区域，2、5区为曲柄销过渡圆角区域，3、4区为连杆轴颈油孔部位。各个区域均考察了最大主应力、最小主应力和等效应力。

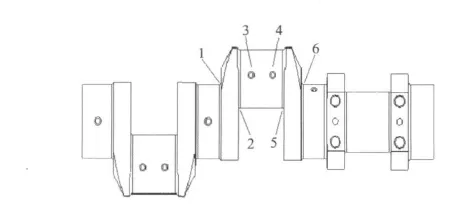
图5 曲轴结构具体考察区域

3.1 曲轴A方案具体考察区域应力值如表2所示。

3.2 曲轴B方案具体考察区域应力值如表3所示。

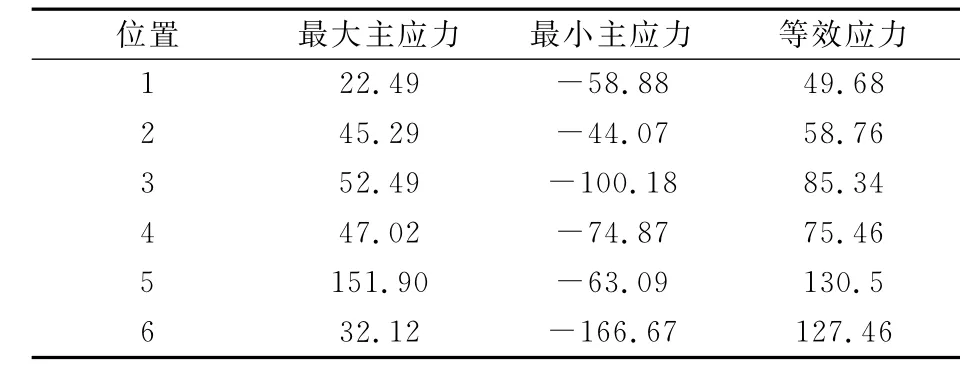
表2 曲轴A方案具体考察区域应力值MPa

表3 曲轴B方案具体考察区域应力值 MPa

3.3 静态安全系数

曲轴采用42CrMoA材料，其屈服极限和强度极限分别为930MPa、1 080MPa［2］，从列表中看到计算所得的等效应力、最大主应力、最小主应力的值均远小于材料的屈服极限和强度极限，按照第一强度理论，曲轴A方案和B方案在静载下的安全系数分别达到6.12和6.88。按照第四强度理论，曲轴A方案和B方案在静载下的安全系数分别达到7.13和7.46。

3.4 疲劳强度安全系数

曲轴单拐平均应力和应力幅最大的部位出现在连杆轴颈下部与曲柄臂夹角处，选取此部位做为疲劳安全系数计算的区域。

非对称循环的弯曲疲劳安全系数可通过式（1）计算［3－4］：

式中σ－1为材料对称循环弯曲疲劳极限，σ－1＝0.45 σb

［4］；σa为应力幅；σm为平均应力；Kσ为弯曲时圆角处的应力集中系数，取1.0；β为强化系数，所分析的曲轴没有采用圆角强化工艺措施，故取β＝1.0［4］；εσ为绝对尺寸影响系数，在文献［4］中查得为0.62；ψσ为材料对应力循环不对称的敏感系数，按式（2）进行计算［4］。

其中σ0为脉动循环时材料的弯曲疲劳极限，取σ0＝（1.4～1.6）σ－1［4］。

通过计算，曲轴A方案和B方案的疲劳强度安全系数分别为2.58和2.90。

4 结论

（1）曲轴A方案和B方案，其静强度满足可靠性要求。

（2）由文献［4］，曲轴规定的疲劳安全系数为1.5～2.0，曲轴A方案和B方案的疲劳强度满足可靠性要求。

（3）通过对比曲轴A方案和B方案的计算结果，可以得出，曲轴B方案其静强度、疲劳强度比A方案都有明显提高，曲轴B方案设计要优于A方案设计。

［1］朱张校.工程材料［M］.北京：清华大学出版社，2001.

［2］闻邦椿.机械设计手册［M］.北京：机械工业出版社，2010.

［3］刘鸿文.材料力学［M］.北京：高等教育出版社，2000.

［4］杨连生.内燃机设计［M］.北京：中国农业机械出版社，1984.