基于分数阶希尔伯特变换的罗音特征提取*

李真真 杜明辉 吴效明

(1.华南理工大学生物科学与工程学院，广东广州510006;2.华南理工大学电子与信息学院，广东广州510640)

肺音中蕴藏了丰富的疾病相关信息.异常肺音的检测方法是当前肺音分析研究的核心内容，其中最主要也是最为重要的异常肺音是罗音，又称间断性音［1］.罗音时域形态为以震荡起始逐步展宽的波形.罗音出现的时刻、单呼吸周期出现的个数以及罗音的分布等特性都与肺部疾病紧密相关.

罗音检测的经典方法有参数估计法和谱估计法［2-4］.参数估计法的优点是简单实用，且易于硬件实现，但它要求信号具有平稳性，而实际的肺音信号不具有平稳性，同时，采用该方法从肺音信号中分离出的罗音实际上混杂了心音、非平稳噪声等其它信号.罗音检测中较为常用的短时谱分析法虽然有一定的检测成功率，但罗音在频域中的特征并不突出，反而在是在时域中具有显著的形态特征.近年来有多种罗音检测方法被提出，其中检测效果较好的有基于小波与人工神经网络的方法，即采用小波做特征提取，再依据神经网络进行分类［5-7］.此外，源于希尔伯特－黄变换的经验模态分解法的效果也很好［8］.现有的罗音检测方法大多理论性很强，但在实际应用中复杂度过高，运算效率低.

分数阶希尔伯特变换是一种新兴的信号处理方法［9-13］.该变换对信号中的异常分量有着高度敏感性，非常适用于分离正常肺音信号中的异常肺音.文中将分数阶希尔伯特变换引入罗音检测，研究了不同分数阶时，该变换作用于罗音信号进行时域上的特征提取及检测的方法.

1 罗音的时域特征

罗音的时域特征非常显著，无论是传统听诊中用人耳来听还是采用时域扩展法显示出来，都是易于辨识的.从发声机理上讲，罗音是气流在传输中遭遇到气道的突然打开或突然闭合而产生的;从波形上而言，罗音的出现一定起始于一个突然的尖锐振荡.Murphy等［14］给出了时域上罗音形态的判定准则.杜明辉等［7］给出了理想的罗音信号模型:

其中，a1=0.5，a2=1.49，a3=0.78，fo=2.0.该模型的时域波形如图1所示.

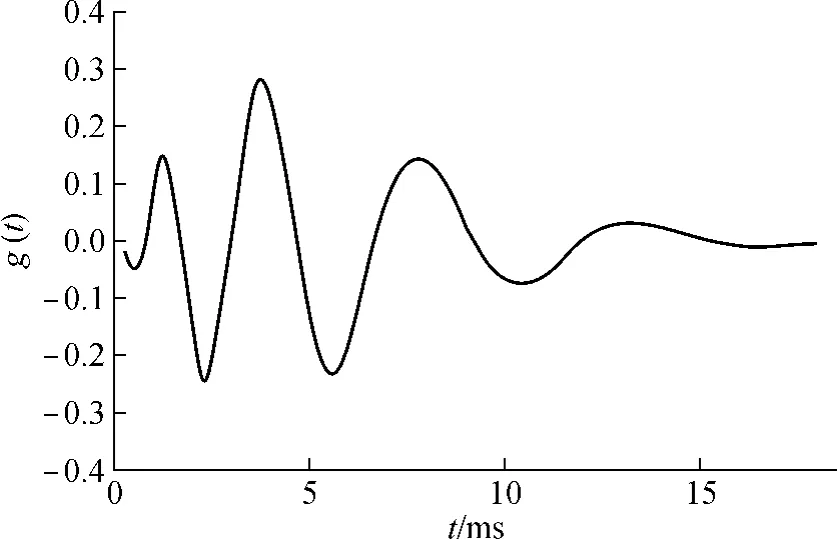
图1 理想罗音信号模型的时域波形Fig.1 Waveform of an ideal crackle signal model in time domain

2 基于分数阶希尔伯特变换的罗音检测

2.1 分数阶希尔伯特变换的定义

分数阶希尔伯特变换源于传统的希尔伯特变换，是在分数阶傅里叶变换的基础上定义的.它既保留了传统希尔伯特变换对突变信号的敏感性，又依托于分数阶傅里叶变换分数阶化后获取的对信号突变信息精细化分析的能力.

分数阶希尔伯特变换最早是由Lohmann等［12］于1996年提出的，其传输函数定义为

式中:FQ为分数阶傅里叶变换，Q为分数阶傅里叶变换的阶数，且φ=P，P为分数阶希尔伯特变换的阶数.

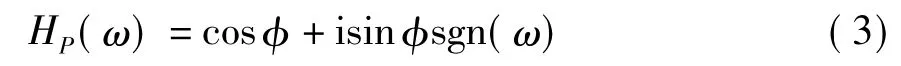
2.2 离散化分数阶希尔伯特变换的实现

式中，

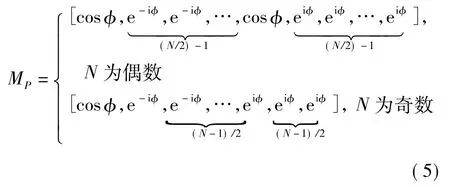
也就是说，分数阶希尔伯特变换作用于信号的过程是:先进行Q阶分数阶傅里叶变换，再乘以模板MP，再通过Q阶逆变换变换回来，之后输出信号y［n］.变换流程如图2所示.由图2可见，分数阶希尔伯特变换简单、快速，易于实现.

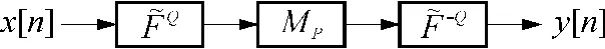
图2 离散化分数阶希尔伯特变换的实现流程Fig.2 Realization flowchart of discrete fractional Hilbert transform

2.3 基于分数阶希尔伯特变换的罗音特征提取

将分数阶希尔伯特变换作用于罗音信号，来探讨其物理意义和时域形态特征.当Q=1时，分数阶傅里叶变换退化为传统傅里叶变换.当P=1时，分数阶希尔伯特变换退化为传统的希尔伯特变换.经典理论中，传统的希尔伯特变换作用于正弦信号，其物理意义是做π/2的相移，在P取不同阶时，分数阶希尔伯特变换作用于正弦信号的物理意义是逐步的相移.

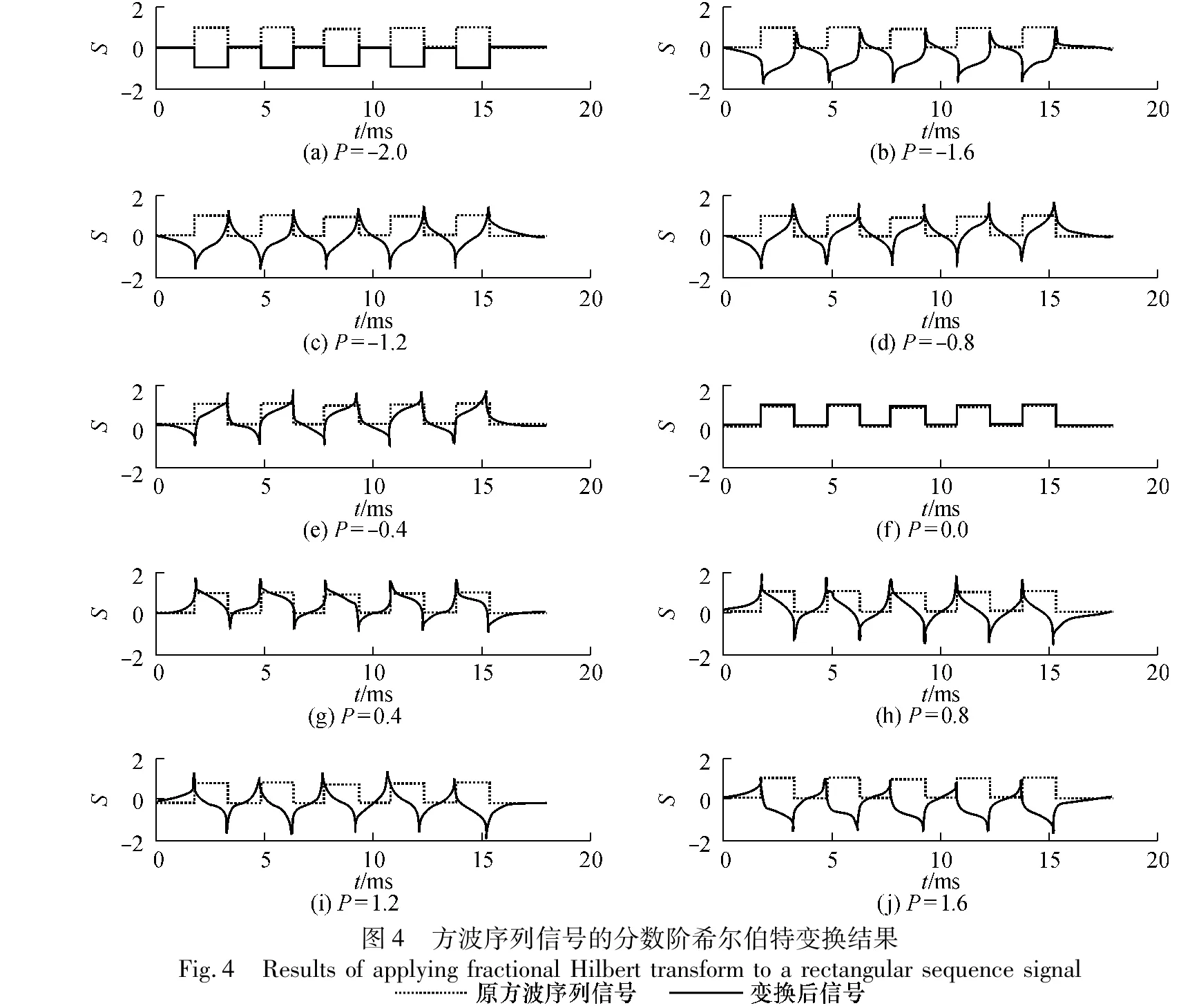
罗音信号在时域上的形态类似于正弦信号，在P取不同阶时，也表现为逐步的相移.以理想的罗音信号模型g(t)为例(参见式(1)及图1)，在Q=1、P取不同阶时，将分数阶希尔伯特变换作用于g(t)，变换后的结果在时域形态上是一系列的逐步相移，如图3所示.图中S表示信号随时间而变的波形.而对于非正弦形态的信号，在不同阶的分数阶希尔伯特变换的作用下，其结果包含了其它形态变化，与正弦形态的信号特征区别显著.以方波序列信号为例，其变换结果如图4所示.

图3(a)－3(j)中，P的阶数从－2.0递增到1.6，递增差值为0.4.由图中可见，分数阶希尔伯特变换作用于信号的周期为4.当P从－2.0增大至2.0时，原信号相位从－π逐步随之增大至π.其中，当P=0.0时(见图3(f))，相当于未对信号做变换，其相移为0.图4中，在不同P取值下，与理想罗音信号做变换的情形相比，原方波序列信号变换后的波形与原方波差别很大，该变换结果类似于对方波边缘做提取.这一结论已经应用于图像边缘提取中，取得了较好的效果［11］.将图3与图4对比可见，在不同分数阶希尔伯特变换的作用下，理想罗音信号和方波序列信号的变换结果差别很大.因此，可以依据罗音信号在时域上类似于正弦信号的形态特点，提取其在不同阶分数阶希尔伯特变换作用下逐步相移的特征来进行罗音检测.

3 实验仿真

文中以不同阶下的分数阶希尔伯特变换作用于罗音，将变换后结果作为特征，利用相关函数法构建了初步的罗音检测系统.因在理想的情形下，罗音的变换结果为原罗音信号的一系列相移，所以将原罗音信号与各阶变换结果做相关函数，以各阶相关函数为待匹配特征组，将其与标准模板相匹配，匹配系数高的判定为检测到罗音，否则判为非罗音，并将检测结果标记出来.

具体而言，对于某一定长度的肺音信号，先进行检测区间划分，即将待检测信号序列划分为若干个可能的罗音区间，其依据是罗音在时域上的突变性.罗音有一个突发振荡的起始，反映在波形上即为相位上的突变，文中先计算输入信号的相位变化，当发生相位突变时(如相位变化大于π/2时)，将该点标记为相位突变点，标记的相位突变点将信号序列分隔为有重叠的一系列子区间，再对每个分隔出的子区间上的波形进行检测.

文中在Matlab的平台上实现了该罗音检测系统，采用通用的美国胸科医学会教学肺音信号进行检测实验.采用Murphy等［14］提出的“时间扩展法”和判定法来验证检测结果.Murphy等［14］指出，判定罗音需要大致满足4个要点:(1)该段波形有3－16个过零点;(2)其振荡最大峰值振幅大于背景的两倍;(3)有一个尖锐的振荡起始;(4)其振荡逐渐展宽.实验信号的采样率为11 kHz，以2000个采样点为一组实验信号序列，共检测了400组.检测正确率为91.2%，检测错误主要是误判与漏判，其中误判与漏判率分别为6.2%和2.6%.误判主要是将形态上类似于正弦信号的肺音信号误判为罗音，漏判主要是在几个罗音连续出现或是有重叠时，由于相位的连续性未能实现准确的区间划分而导致的.文中方法的检测正确率与近年新兴的若干方法的［2-7］相当.与基于非平稳信号处理的检测方法相比(如文献［4］)，文中方法不需要进行最后的人工判别，实现了计算机自动识别.

图5(a)－5(d)给出了4组实验结果，其中上图为原肺音信号，下图为检测结果，以细竖线标记罗音出现的时刻，细竖线出现的数目表明罗音出现的数目.图中L表示标记出罗音出现的时间点的序列.由图5可见，基于分数阶希尔伯特变换的方法可以有效地提取罗音特征，进行罗音检测，检测结果较为理想.典型的误判情形如图6(a)所示，图中粗竖线标记一次误判情形，标记处的肺音信号形态上非常类似于正弦信号，但该部分信号没有振荡起始，不是罗音，因此为误判.一种漏判的情形如图6(b)所示，虚线标记处应检测出罗音，但由于3个罗音连续叠加，相位连续，所以出现漏判.

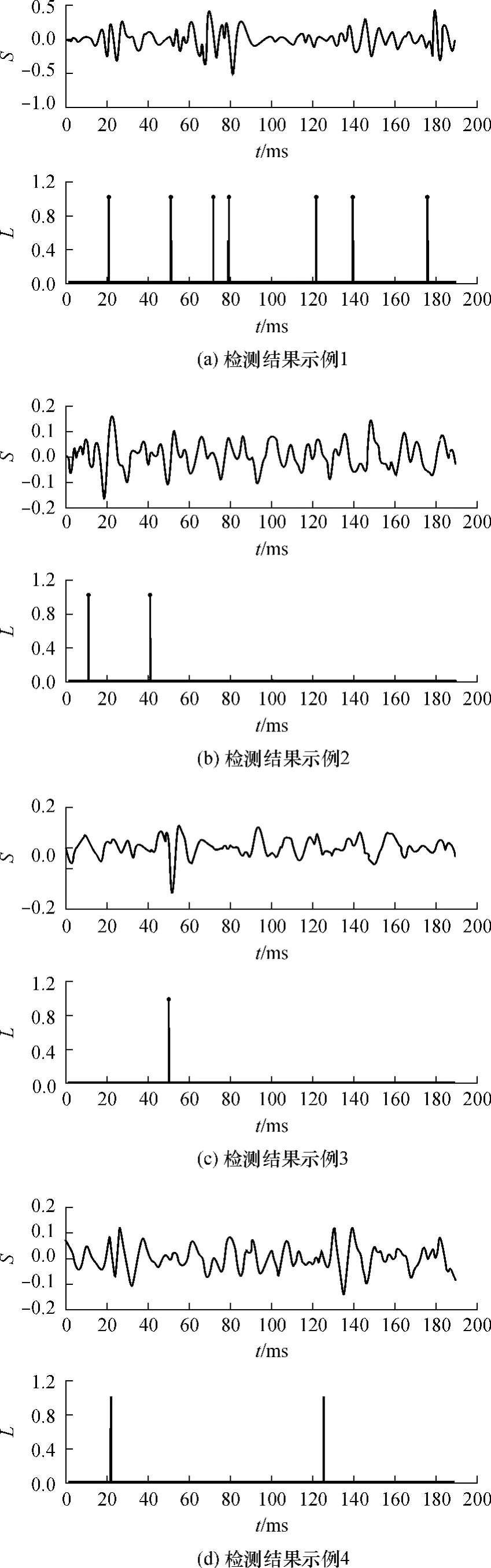
图5 罗音检测结果示例Fig.5 Some crackle detection results

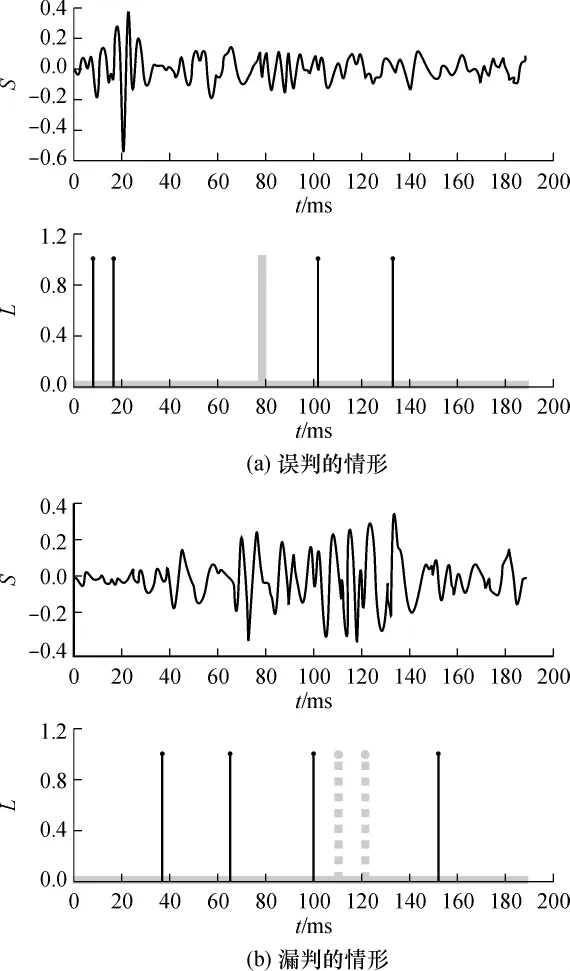
图6 罗音检测误判与漏判示例Fig.6 Examples of false and missing crackle detections

4 结语

文中分析了分数阶希尔伯特变换应用于罗音检测的可行性，并进行了实验验证.结果表明，罗音信号在不同阶分数阶希尔伯特变换作用下的特征显著，初步罗音检测系统验证了分数阶希尔伯特变换对罗音信号特征提取的有效性.

在分数阶希尔伯特变换作用于罗音信号后，采用相关函数法并不能充分地表征出变换后的罗音特征.在进一步的研究中，还可以考察更为有效的表征手段，以提高罗音检测系统的性能与效率.

［1］Gavriely N.Breath sounds methodology［M］.Boca Raton:CRC Press，1995:18-22.

［2］Dorantes G，Charleston S，Gonzalez R，et al.Crackles detection using a time-variant autoregressive model［C］∥30th IEEE Engineering in Medicine and Biology Society Conference.Vancouver:IEEE Engineering in Medicine and Biology Society，2008:1894-1897.

［3］Kaisla T，Sovijarvi A，Piirilla P，et al.Validation method for automatic detection of lung sound crackles［J］.Medical＆ Biological Engineering ＆ Computing，1991，29(5):517-521.

［4］Ono M，Arakawa K，Mori M，et al.Separation of fine crackles from vesicular sounds by a nonlinear digital filter［J］.IEEE Transactions on Biomedical Engineering，1989，36(2):286-288.

［5］Kandaswamy A，Kumar C S，Ramanathan R P，et al.Neural classification of lung sounds using wavelet coefficients［J］.Computers in Biology and Medicine，2004，34(4):523-537.

［6］刘毅，张彩明，赵玉华，等.基于多尺度小波包分析的肺音特征提取与分类［J］.计算机学报，2006，29(5):769-777.Liu Yi，Zhang Cai-ming，Zhao Yu-hua，et al.The feature extraction and classification of lung sounds based on wavelet packet multiscale analysis［J］.Chinese Journal of Computers，2006，29(5):769-777.

［7］杜明辉，孙军良，陈荣昌.基于匹配子波变换的呼吸罗音检测与分类［J］.生物医学工程学杂志，1998，15(4):400-405.Du Ming-hui，Sun Jun-liang，Chen Rong-chang.Crackle detection and classification based on matched wavelet transform［J］.Journal of Biomedical Engineering，1998，15(4):400-405.

［8］Li Z Z，Du M H.HHT based lung sound crackle detection and classification［C］∥International Symposium on Intelligent Signal Processing and Communications Systems.Hong Kong:The Chinese University of Hong Kong，2005:385-388.

［9］Ran Tao，Li Xue-mei，Wang Yue.Generalization of the fractional Hilbert transform ［J］.IEEE Signal Processing Letters，2008，15:365-368.

［10］Pei S C，Yeh M H.Discrete fractional Hilbert transform［J］.IEEE Transactions on Circuits and Systems—Ⅱ:Analog and Digital Signal Processing，2000，47(11):1307-1311.

［11］Davis J A，McNamara D E，Cottrell D M，et al.Analysis of the fractional Hilbert transform ［J］.Applied Optics，1998，37(29):6911-6913.

［12］Lohmann A W，Mendlovic D，Zalevsky Z.Fractional Hilbert transform ［J］.Optical Letters，1996，21(4):281-283.

［13］Zayed A I.Hilbert transform associated with the fractional Fourier transform ［J］.IEEE Signal Processing Letters，1998，5(8):206-208.

［14］Murphy R L，Holford S K，Knowler W C.Visual lungsound characterization by time-expanded wave-form analysis［J］.The New England Journal of Medicine，1977，296:968-971.