多层结构局部延性与整体延性需求关系解析*
周靖 方小丹
(1.华南理工大学亚热带建筑科学国家重点实验室,广东广州510640;2.华南理工大学建筑设计研究院,广东广州510640)
现有的抗震设计方法注重结构构件及局部的内力计算和级差分配,可有效防控结构局部的脆性破坏,但对控制结构整体的位移破坏模式尚有欠缺.新修订的混凝土结构设计规范[1]明确提出以构件计算为主适当扩展到整体结构的抗倒塌设计.在日渐重视的体系能力抗震设计方法中,把握结构构件延性到整体延性需求的协调匹配关系、确定合理的输入设计地震作用是开展以构件计算为主适当扩展到整体结构抗震设计的有效途径.
结构局部与整体延性需求关系是指建筑结构中的梁、柱、墙体、楼层以及整体之间的抗震延性需求协调匹配模式,能体现结构抗震延性需求的空间分布规律和层次性,也是确定输入设计地震作用的参考指标[2-3].局部延性需求应用于结构的极限破坏评估,而系统延性需求应用于结构反应修正系数的标定[4].考查结构整体与楼层位移需求以及楼层位移与构件弹塑性变形需求之间的关系是基于性能/位移抗震设计方法的研究主题之一,这一研究的扩展是探讨结构整体与局部的抗震延性需求关系[5].建立结构系统延性需求与结构关键部位单元延性(曲率延性)需求的关系,再从单元延性需求落实到保证延性的构造措施,是有效实现机构控制的途径.但是,从抗震延性需求方面探究构件、楼层以及整体之间的协调匹配关系,明确抗震延性能力层次性的研究尚不多.欧洲规范[2]要求根据不同结构体系以及性能系数设计的结构单元和系统应具有足够的延性能力,为此,给出了杆件曲率延性与结构基本性能系数之间的定量关系(等效于单元与整体的延性需求协调关系)来直接检验和控制结构局部与系统延性需求之间的协调匹配关系.澳洲抗震设计指南[6]提出采用具有一定延性水平的整体结构屈服机制的设计思路,强调从结构系统保证预期机制的实现,同时评估单元与系统延性的协调.Gioncu[7]分析了影响钢框架结构局部延性和系统延性需求的因素以及局部延性和系统延性的关系,强调抗震能力设计方法中,直接检查和控制结构以及单元延性需求的方法尚有待发展.Tasnimi和 Bojorquez等[8-9]分析了钢框架结构单元与整体延性需求之间的相互制约关系,分别建立了两者简单的统计关系.Biondini等[10]分析了多层混凝土框架结构柱的延性与整体延性需求的关系,指出局部与整体延性需求的关系与结构的极限倒塌屈服机制相关.Song等[4]研究了多高层钢框架结构延性需求关系,发现虽然系统延性需求基本相同,但“弱柱强梁”型结构比“强柱弱梁”型结构的构件延性需求明显要大,而且结构中屈服破坏的部位有很大的差异.Kunnath等[11]研究了框架结构杆件、楼层和系统延性需求,指出局部延性需求大于楼层延性需求,柱延性需求大于梁延性需求.Cosenza等[12]基于静力加载的方法建立了多层混凝土结构构件与整体结构延性需求的粗略关系.在国内,赵艳静等[13]基于完全的梁铰侧移机构框架系统建立了框架梁柱曲率延性与系统延性需求的关系.
国内外现有的相关研究主要是统计分析多层钢框架和混凝土框架结构的延性需求关系;而探究结构抗震延性需求协调匹配模式、解析单元延性到结构延性层次性的研究鲜见报道,单元和系统延性需求关系认知的深度和广度很有限,尚有待展开深入研究.由于缺乏用于直接检查和控制混凝土结构单元和整体延性需求关系的量化表达,因此结构单元层次的延性设计基本难以开展.鉴于此,文中在合理的模型结构假定基础上,通过理论分析方法,推导了多层结构整体、楼层以及框架柱或墙单元位移延性需求的简化解析关系.研究结果在指导结构初步设计和快速评估结构的刚度分布和延性分布方面具有一定的工程价值.
1 楼层与整体延性需求关系解析
假定多高层结构楼层以及柱(或墙)为弹簧联系系统(如图1所示,图中h为楼层高度,l为柱跨距,wi为质点i的重量),通过理论分析推导结构局部与整体延性需求关系的解析结果.

图1 弹簧联系系统模型Fig.1 Models of spring link system
采用简单的两质点体系(见图1(a),相当于两个弹簧的串联系统),假定底层为薄弱层,整体刚度为Kw,二层为强度较大楼层,整体刚度为Ks;假定楼层力-位移曲线为理想弹塑性关系,薄弱层的屈服强度Vw,y小于二层的屈服强度Vs,y.由以上基本假定可得两质点结构系统的屈服强度为

式中:Vs表示二层未屈服前的某一强度,Vs<Vs,y;Ds表示二层未屈服前的某一相对位移,Ds<Ds,y,Ds,y表示二层的屈服位移.
由式(1)得到

薄弱层的屈服位移

系统屈服位移为

在侧向荷载作用下,系统经历弹塑性变形,顶点峰值位移Dmax由底层质点的峰值位移Dw,max和二层质点的峰值位移Ds,max组成:

二层为强度较大楼层,假定峰值位移不超越屈服位移,有

薄弱层局部延性系数μL和整体结构延性系数μG分别为

将式(4)和(5)代入式(8),有


将式(6)和(7)代入式(10),有

将式(2)代入式(11),有

当系统进入弹塑性变形阶段(μG≥1)时,式(11)给出了薄弱层局部延性与整体延性需求的关系:薄弱层局部延性需求大于整体结构的延性需求.由式(12)设定两质点系弹簧的刚度比,延性需求关系的量化表达如图2(a)所示(图中曲线是将式(12)取等号,按最大情况给出的).由图2可见:整体延性系数增加,局部延性系数增大,但增大的幅度逐渐减小;底层与二层的刚度比增加,局部延性系数增大.
当薄弱层滞回曲线是双线性型时,屈服后刚度用CRKw表达,式(12)取等式,则可改写为

将式(13)变换为

式(14)表明,薄弱层屈服后刚度系数CR对局部与整体延性需求关系有一定的影响.虽然延性需求关系变化趋势相同(见图2(b)),但随着CR的增大,局部延性系数减小(见图2(c)),而且表现为明显的非线性变化趋势.
当系统质点数增加,而且增加的质点弹簧与二层质点弹簧性质(假定不屈服)相似时,基于相似的推导,式(12)可表达为

式中,Ksi表示强度较大的第i层的刚度.
对楼层屈服后的刚度硬化系统,将式(14)中的Ks改写为等效刚度Kse:

式(15)表明,对于给定的整体延性需求,在楼层系统中增加相对于薄弱层不发生屈服的较强楼层时,薄弱层的延性需求将增大;而且对薄弱层在结构系统中的位置并没有影响.
以上分析表明:薄弱层延性与整体延性需求的关系依赖于楼层侧向刚度与其它楼层串联组合刚度之比,串联组合刚度与薄弱层刚度比越大,局部延性需求越大;增加楼层数,薄弱层局部延性需求增大.
2 柱或墙单元与楼层延性需求关系解析
采用单跨双柱体系(见图1(b),相当于两个弹簧的并联系统).弱柱刚度为抗侧屈服强度为强柱(或墙)刚度为抗侧屈服强度为根据一般情况假定且假定楼面梁刚度无穷大,柱单元的侧移力-位移曲线为理想弹塑性关系.弱柱单元和系统的延性系数分别为

图2 楼层局部与整体延性需求关系Fig.2 Relationship between storey and global ductility demand

当楼面梁刚度无穷大时,弱柱单元的最大位移等于楼层整体位移,则有

将式(17)和式(18)代入式(19),有

式(20)表明,楼层中柱单元与楼层的延性需求关系与屈服位移相关.柱单元的屈服位移能明确地通过计算确定,因此,柱单元与楼层延性需求关系的确定主要依赖于楼层屈服模式和屈服位移的认定标准.在侧向荷载作用下,假定弱柱单元屈服即认定楼层屈服,即有

在侧向荷载作用下,假定强柱(或墙)单元屈服才认定为楼层屈服,强柱与弱柱屈服位移关系如图3所示,图中Vz、Dz分别表示柱的强度和位移分别表示强柱和弱柱的强度表示强柱的屈服位移.依据该关系可确定延性需求关系的大致范围.依据前述假定式(20) 变换为
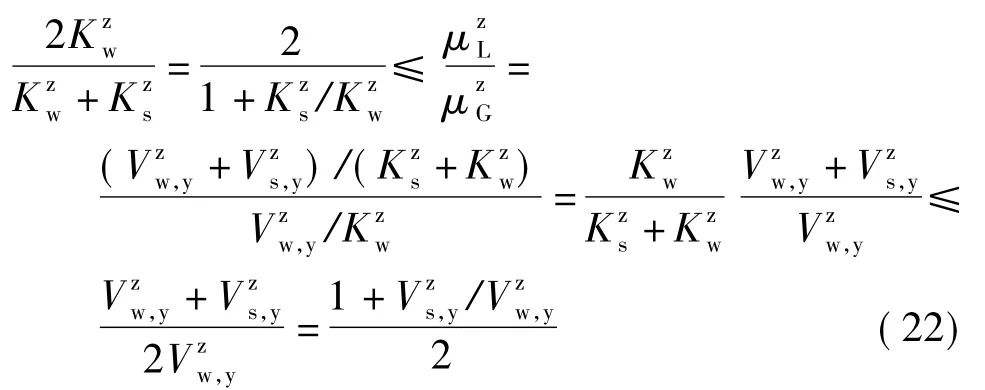
即



图3 强柱和弱柱单元的刚度和强度比例关系Fig.3 Strength and stiffness relationship between strong column and weak column


图4 弱柱单元与楼层延性需求的关系Fig.4 Relationship between weak column element and storey ductility
弱柱单元和楼层延性需求关系的量化表达如图4所示.由图4和式(23)可知:弱柱单元延性与楼层延性的需求关系跟楼层强弱柱的刚度比及抗侧屈服强度比相关;刚度比越大弱柱延性需求越小,强度比越大弱柱延性需求越大.由图4和式(25)可知,一般情况下(n>2),对给定的整体延性系数,在系统中增加一个柱单元,对上限的情况,弱柱的延性需求将增大,且增大的幅度变小;对下限<情况,弱柱的延性需求将减小,且减小的幅度变小.
3 数值算例验证
采用2榀平面混凝土框架结构进行算例解析.两跨六层混凝土框架结构立面见图1(a),水平跨度均为5.0m,框架梁为300mm×600 mm;框架KJ1楼层高度为(4.0+5@3.0)m,框架柱截面均为500mm×500mm;框架KJ2楼层高度为(3.0+5@3.0)m,框架柱截面除底层中间柱为400mm×500mm之外,其它柱截面均为500mm×500mm,所有框架柱的配筋数均为820,两侧对称布置;结构设计基本参数特性及计算结果见表1.利用美国中部地震工程研究中心结构弹塑性分析软件Zeus-NL[14]进行静力Pushover分析,屈服位移按等能量面积法确定,极限位移取最大承载力下降15%对应的位移值,此外,KJ2取一个超过极限位移、与KJ1具有相同整体延性水平的延性系数(μG=4.63),用于两者的比较.估算结果底层最不利延性系数按式(14)和(16)计算,取CR=0.1,结构整体延性系数采用程序分析的结果.
对于给定的整体结构延性系数μG=4.63,比较表1中的楼层延性系数计算结果(KJ2的第2行与KJ1)可知,楼层刚度越大局部延性系数越大,其主要原因是在楼层抗侧承载力基本相等的情况下,刚度越大屈服位移越小,延性需求增大.KJ2的整体延性系数(μG=3.89)比 KJ1的(μG=4.63)小,但 KJ2的局部延性系数(μG=14.29)比 KJ1的(μG=13.59)大,表明整体延性需求较小时,若刚度分布不合理,有可能出现大的局部延性需求.
以KJ2为分析对象,计算框架柱单元延性与楼层延性的关系.考虑截面实际配筋及重力荷载代表值计算的边柱和中柱抗剪承载力分别为296.9 kN和212.2kN.采用式(25)上限计算的中柱单元延性与楼层延性需求比为1.266,按程序分析的延性需求比为1.143.
比较估算的最不利延性系数与程序分析延性系数的结果可知,两种计算方法的整体结果是相同的,而局部延性系数估算结果一般比程序分析结果大,差异主要源于模型假定与程序分析情况的差异,如底层屈服后,二层、三层很快也会出现屈服;此外,快速估算结果均为最不利的上限情况,因此,两种计算的结果也会有差异.鉴于此情况,运用估算方法时可以在估算结果的基础上,采用一个小于1.0的系数进行修正,此修正系数的确定尚有待开展大量的统计分析.
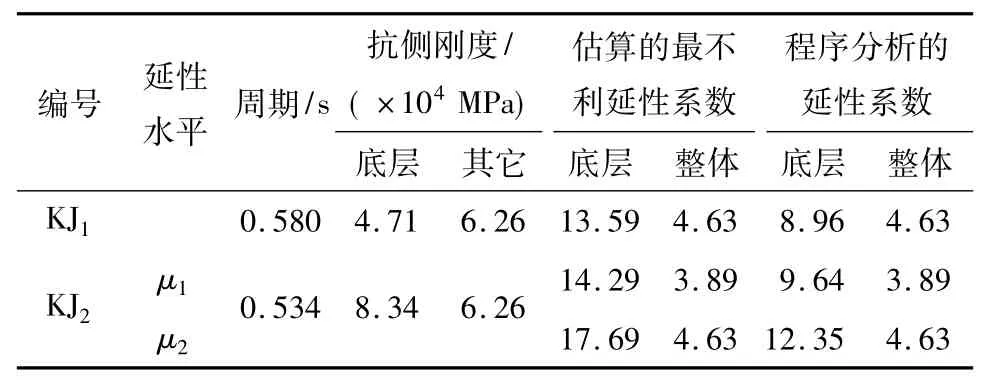
表1 数值算例结果Table 1 Results of numerical examples
4 结论
(1)多高层结构体系中,局部楼层延性需求比整体延性需求大.
(2)薄弱层延性与整体延性需求的关系依赖于楼层侧向刚度与其它楼层串联组合刚度之比,串联组合刚度与薄弱层刚度比越大,局部延性需求越大;增加楼层数,薄弱层局部延性需求增大;楼层屈服后的刚度对薄弱层延性与整体延性需求的关系也有重要影响.
(3)弱柱单元延性与楼层延性需求关系跟强弱柱的刚度比以及抗侧屈服强度比相关,刚度比越大弱柱延性需求越小(下限),强度比越大弱柱延性需求越大(上限).
[1]GB 50010—2010,混凝土结构设计规范[S].
[2]Euro code 8:design of structures for earthquake resistance,part 1:general rules,seismic actions and rules for buildings[S].
[3]Nassar A A,Osteraas J D.Seismic design based on strength and ductility demand[C]∥Proceedings of the Tenth World Conference on Earthquake Engineering.Madrid:Taylor& Francis,1992:5861-5866.
[4]Song J K,Yun C B.Estimation of system-level ductility demands for multi-story structures[J].Engineering Structures,1997,19(12):1025-1035.
[5]Gupta A,Krawinkler H.Relating the seismic drift demands of SMRFs to element deformation demands[J].Engineering Journal,2002,39(2):100-108.
[6]AS/NZS 1170.4, Austra-lian/New Zealand standard,structural design action-part 4 earthquake actions[S].
[7]Gioncu V.Ductility criteria for steel structures[J].Journal of Constructional Steel Research,1998,46(3):443-444.
[8]Tasnimi A A,Mahmoodi M.Relationship between global and local ductility for low-rised RC-MRF[C]∥Proceedings of the Second International Conference on Earthquake Hazard and Seismic Risk Reduction.Yerevan:Springer,1998:15-21.
[9]Bojorquez E,Diaz M A,Ruiz S E,et al.Correlation between local and global cyclic structural capacity of SMR frames[C]∥First European Conference on Earthquake Engineering and Seismology.Geneva:European Association of Earthquake Engineering,2006.
[10]Biondini F,Toniolo G.Seismic behaviors of concrete frames:experimental and analytical verification of Eurocode 8 design rules[C]∥Fib Symposium on Concrete Structures in Seismic Regions.Athens:International Federation for Structural Concrete,2003:1-12.
[11]Kunnath S K,Kalkan E.Evaluation of seismic deformation demands using non-linear procedures in multistory steel and concrete moment frames[J].ISET Journal of Earthquake Technology,2004,41(1):159-181.
[12]Cosenza E,Manfredi G.Damage indices and damage measures[J].Progress in Structural Engineering and Materials,2000,2(1):50-59.
[13]赵艳静,陈云霞,于顺泉.钢筋混凝土异形截面框架柱轴压比限值的研究[J].天津大学学报,2004,37(7):600-604.Zhao Yan-jing,Chen Yun-xia,Yu Shun-quan.A research on limited value of axial compression ratio of arbitrarily shaped RC columns[J].Journal of Tianjin University,2004,37(7):600-604.
[14]Elnashai A S,Papanikolaou V K,Lee D H.Zeus-NL—A system for inelastic analysis of structures user manual[CP/OL].(2006-01-01)[2011-05-11].http:∥mae.cee.uiuc.edu/software_and_tools.

