梁柱结构协同作用的车辐式索杆体系成形分析*

赵俊钊 陈务军† 潘钦 付功义

(1.上海交通大学空间结构研究中心，上海200030;2.上海太阳膜结构有限公司，上海201611)

车辐式张力结构是由受拉索和受压杆组成的空间预应力结构，具有造型轻盈、传力简单明确、跨度大等优点，近些年来在大型公共建筑中得到了广泛应用.大型工程中常见的车辐式张力结构主要构件包括外压环、内拉环以及内外环之间的索杆体系，文献［1］给出了几种常见的车辐式张力结构样式.

车辐式张力结构依靠预应力提供结构刚度，是一种强几何非线性结构［2］.该类结构通常采用整体张拉成形的方法进行结构施工，施工过程属于大位移、小应变问题，同时伴随有机构位移.因此，对这类结构的施工分析同样是一个强几何非线性问题.结构成形过程包含多个中间平衡状态，每一平衡状态下都有内力与位形的对应关系，内力的变化将牵动位形的变化，同样位形的变化也会带来内力的变化，内力与位形相互耦合.这种“力”与“形”密不可分的关系，决定了这类结构的设计、制作、施工必须环环相扣，应当是一体化的综合过程.施工过程中，各结构单元无应力长度和结构拓扑关系一定，通过不断缩短牵引索使结构就位.此外，周边结构并非完全刚性，在索杆体系提升过程中，周边结构必然产生位移，此位移会对中央索杆体系的状态产生影响，而周边结构位移的大小由周边结构整体刚度和索张力大小决定.

车辐式张力结构在施工过程中属于几何可变体系，其几何不稳定性直接导致了体系刚度矩阵奇异，造成传统有限元法的数值计算困难.因此，该类结构施工过程的形态分析和相应技术一直未能有效解决.车辐式张力结构张拉成形分析的每个施工步骤实际为已知单元无应力长度的体系在单元自重和节点荷载作用下的平衡形态的确定问题.

近来有不少关于索杆张力结构施工成形的研究.文献［3］利用通用有限元软件ANSYS，采用生死单元法对宝安体育场屋盖系统进行了施工模拟分析;文献［4］提出施工控制反分析法，对索穹顶结构成形过程进行了研究;文献［5］采用广义逆理论处理刚度矩阵奇异问题，收敛性较差，且需假定运动约束向量;文献［6］假定索为直线刚体杆单元，且假定机构位移;文献［7］提出的求解策略受给定初始坐标的限制;文献［8］未考虑周边结构影响.

以往张力结构应用动力松弛法［8-9］的局限性在于:(1)只用于找形分析和结构分析;(2)索单元全部被理想化为直线杆单元;(3)不考虑边界条件的影响.文中将曲线单元动力松弛法引入张力结构施工过程分析中，采用抛物线单元模拟索，直线杆单元模拟飞柱，提出了一种考虑周边结构协同作用的车辐式张力结构成形分析的新方法.

1 动力松弛法基本方程

结构振动过程也是能量耗散的过程，直到总动能完全耗散达到静力平衡状态.

在振动过程中任意时刻t，任意节点i在x方向的动力平衡方程为［10］

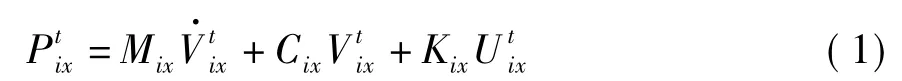
考虑在时间增量Δt内节点速度线性变化，节点速度用中心差分表示为

在时间增量Δt内，通过节点速度的线性内插可以得到节点加速度为

将式(3)、(4)代入式(2)，并取Cix=0，可得

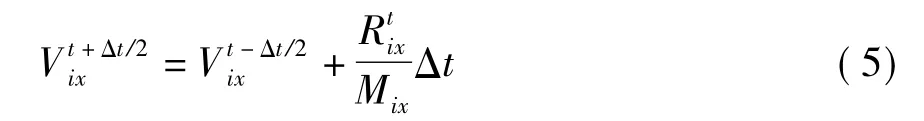
假定结构在t=0时刻从静止状态开始振动，即按直线差分可得因此，在t+Δt时刻，节点i在x方向上的节点坐标和节点位移分别为

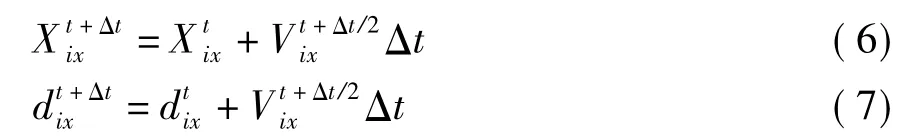
当系统动能达到最大时，所有节点速度置零，从新的结构位置重新开始计算，直到节点不平衡力向量满足收敛条件.

2 索、杆单元节点不平衡力列式

索、杆单元节点不平衡力列式推导过程的基本假定为:单元始终处于弹性阶段，符合虎克定律;索只受拉力而不受压和弯;单元之间为铰接节点;索段上横向荷载沿弦长均匀分布;杆单元自重平均分配到两端节点上.

2.1 索、杆单元变形协调方程

如图1(a)所示编号为k的空间杆单元，单元两端节点分别为i、j，rk为单元弦长.在整体坐标系下杆单元变形协调方程为

式中:f为单元轴向力，Δs＜0时f为压力，Δs＞0时f为拉力;E为材料弹性模量;A为单元截面面积;s0为单元无应力长度;s为单元当前长度.如图1(b)所示编号为k的空间索单元，单元两端轴向力分别为fi和fj，θi、θj分别为索端轴向力与其水平分量的夹角，qk为索承受的沿弦长均布荷载.定义其局部坐标系Oxz，其中x轴平行于索在整体坐标系OXYZ的XY平面的投影线，z轴与Z轴平行，且方向相同.

图1 杆单元和索单元Fig.1 Link and cable elements

根据悬索结构的基本理论［11］，单索在沿弦长均布荷载作用下的平衡形状为抛物线，且抛物线方程为(为简化，以下公式中略去图1(b)所示的变量下标k)

式中:r为索单元两端节点的直线距离，即曲线索单元的弦长;h为索端节点张力f的水平分量，因为索段上无纵向荷载作用，所以h在索段内为常量;l为索单元两端节点的水平距离;c为索单元两端节点的z向距离.

由张力产生的索单元轴向伸长量可按下式近似计算:

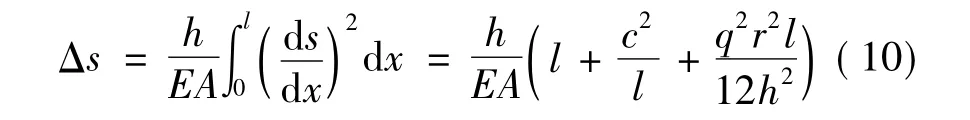
索单元当前长度s按下式近似计算:

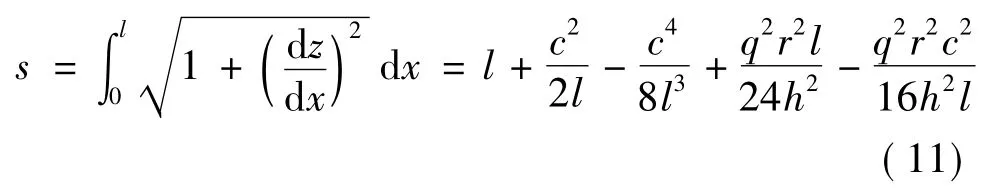
将式(10)、(11)代入关系式s-Δs-s0=0，同时取w=qr可得

式(12)即为无应力长度为s0的索在其自重作用下的变形协调方程，它反映索水平力h、形状参数c和l，以及单元弹性模量E和截面积A之间的关系.如果节点坐标和构件特性确定，则式(12)为关于未知量h的三次方程.

2.2 索、杆单元节点不平衡力列式

如图2所示，索单元k通过节点i与杆单元m和n相连，fn与fm分别为杆单元m和n的轴向力.

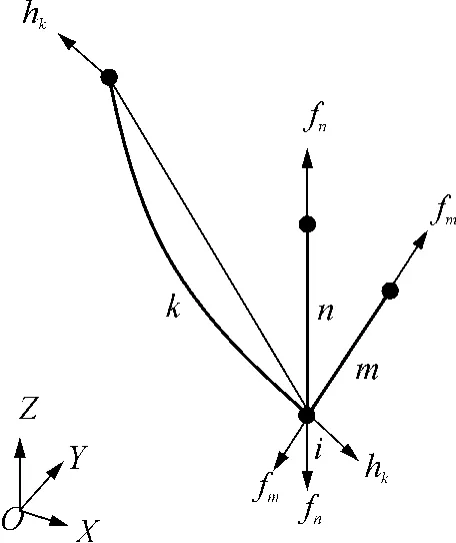
图2 索杆节点Fig.2 Node of cable and strut

以单元内力为未知量的节点i的平衡方程为(为保持索与杆形式的一致性，对索取f=hr/l)

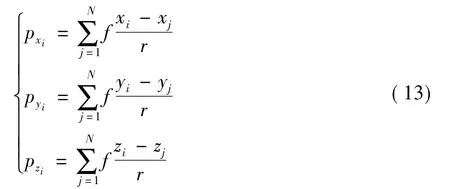
式中，xi、yi、zi为节点i在整体坐标系中的坐标，pxi、pyi、pzi为节点荷载，N为与节点i相连的单元总数.

依次对索杆体系每个节点建立如式(13)所示的平衡方程，并集合成总平衡方程

式中:A为平衡方程未知数的系数矩阵，称为平衡矩阵;f为单元内力列向量;r为单元弦长列向量;P为节点荷载列向量.

通过式(14)可得到索、杆单元节点不平衡力列式:

式中，R为索、杆单元节点不平衡力向量.

3 统一节点不平衡力列式

统一节点不平衡力列式推导过程的基本假定为:单元始终处于弹性阶段;索单元与梁单元为铰接节点;考虑周边结构的几何非线性.

车辐式张力结构的周边结构一般包含大型环梁、立柱、柱间支撑等.中央索杆体系提升以前，周边结构安装位置确定;中央索杆体系提升过程中，索、杆单元无应力长度不变，索张力作用使周边结构产生位移，周边结构位移反过来会影响中央索杆体系的状态.周边节点几何模型与节点不平衡力模型如图 3 所示，其中，Λtt，x、Λtt，y和 Λtt，z分别为节点在x、y和z方向的线位移向量;Rtt，x、Rtt，y和Rtt，z分别为周边结构体系在x、y和z方向的节点不平衡力向量.

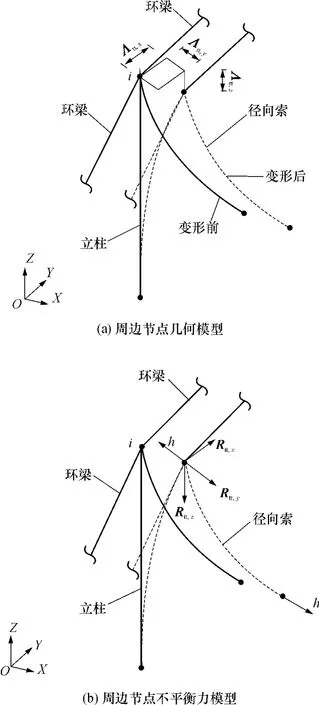
图3 周边节点几何模型和不平衡力模型Fig.3 Geometrical model and unbalanced force model of perimetric nodes

周边节点为梁、柱、索连接节点，梁和柱具有空间6自由度，基于局部坐标系，可列梁、柱内力方程，通过整体坐标变换，建立节点在整体坐标下的节点平衡方程［12］.因内部索杆节点为3自由度，仅线位移连续，为便于整体节点不平衡力列式统一和求解，将周边节点平衡方程写为线位移、角位移分组分开的分块形式:

式中:Ktt、Ktr、Krt和Krr为总节点刚度矩阵的各分块子矩阵;Λtt为周边节点线位移向量，通过式(7)求解;Λrr为周边节点角位移向量;Ftt和Frr分别为综合节点力和节点弯矩;Rtt和Rrr分别为节点不平衡力和节点不平衡弯矩，对于周边节点Rrr=0.

按矩阵乘法展开式(16)，得

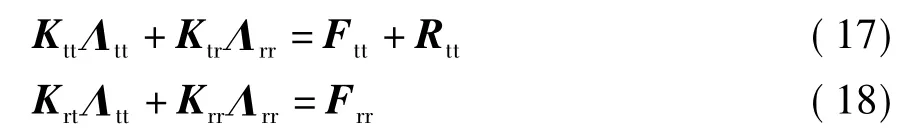
由式(18)求得周边节点角位移为Λrr=K-1rr(Frr-KrtΛtt)，代入式(17)，得到周边结构产生的周边节点不平衡力为

组合式(15)和(19)，便可得到考虑周边结构协同作用的统一节点不平衡力列式:

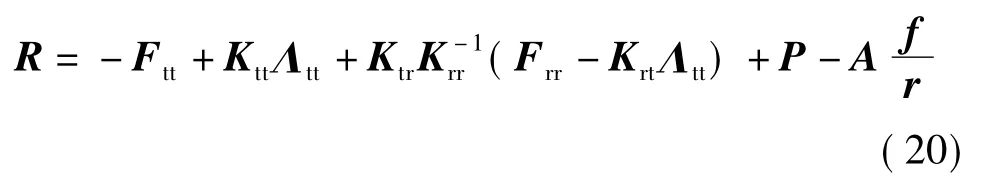
4 求解策略

统一节点不平衡力列式建立以后，采用动力松弛法求解结构平衡状态，通过缩短主动索牵引长度可以得到张拉成形过程的中间平衡状态及最终平衡状态，具体算法如下:

(1)给定周边结构的几何模型和构件属性，计算周边结构刚度矩阵.

(2)给定单元无应力长度向量s0，主动索还包含牵引索长度s1，按式wk=qs0计算各索单元自重并生成向量w;给定索杆几何拓扑关系、初始节点坐标X0、单元截面积和弹性模量.

(3)节点速度、动能置零;给定虚拟质量矩阵M;确定时间增量Δt.

(4)根据当前节点坐标向量，计算坐标差向量l和c.

(5)根据变形协调方程(8)、(12)计算向量f.

(6)按式(19)计算周边节点不平衡力Rtt.

(7)按式(20)计算统一节点不平衡力向量R.

(8)按式(5)计算速度向量Vt+Δt/2，计算节点位移并更新节点坐标.

(9)判断系统动能是否到达峰值，若动能到达峰值，返回步骤(3).

5 算例分析

5.1 宝安体育场结构概况及张拉方案

深圳市宝安体育场是2011年世界大学生运动会足球场，屋盖结构形式为轴对称马鞍形车辐式张力结构，最大跨度为230 m，周边结构和屋盖结构如图4所示.

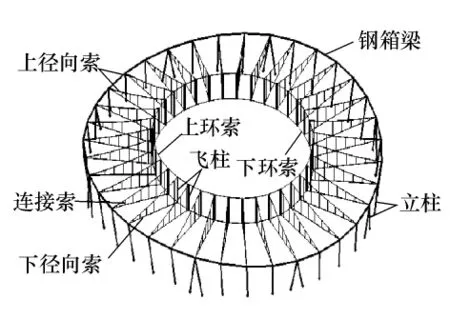
图4 深圳市宝安体育场周边梁柱体系和屋盖Fig.4 Perimetric beam-column assembly and roof of Shenzhen Baoan Stadium

周边结构由立柱和环梁组成;屋盖结构由上下内拉环、受压飞柱、辐射状的径向索桁架和周边强大的压力钢环组成.其中，外压环为内设加劲肋的单层钢箱梁;内拉环为双层索环，上下环索通过无应力长度为18m的飞柱相连;内外环通过36榀索桁架相连，索桁架上下径向索呈凹形布置，上下径向索之间通过受拉连接索相连.在屋盖系统中，上下径向索、飞柱和上下环向索为主要受力构件，上下径向索之间的连接索为次要构件.

成形过程分析与施工张拉方案一一对应，所以文中只介绍施工单位采用的整体张拉施工方案.施工单位所采用的整体施工方案为:先张拉上径向索，再张拉下径向索.根据该施工方案，关键施工过程如下:(1)在地面上拼接上径向索和上环索，分步张拉上牵引索使=0.25 m;(2)安装飞柱、下环索和下径向索，此时下径向索的牵引索长度为8m;(3)张拉上牵引索长度至0m;(4)分步张拉下牵引索至=0m;(5)安装连接索.

5.2 计算参数设置

每根径向索分为8个索单元，在与连接索交点处划分;环向索在每榀索桁架之间为一个索单元;每个飞柱为1个杆单元;连接索用杆单元模拟.该屋盖系统包括648个索单元、288个杆单元和612个节点.成形过程中，径向索与环向索节点重量通过施加节点荷载考虑，在上层节点和下层节点上分别施加重力方向节点荷载13kN和15kN.

上下牵引索通过增加上下径向索的无应力长度来模拟，当上下径向索无应力长度为结构最终状态下的无应力长度时，上下牵引索长度变为0 m，例如当牵引索牵引长度为0.25m时，径向索当前无应力长度等于径向索最终状态无应力长度加上0.25m.

屋盖结构截面形式在表1中列出.索弹性模量为165GPa，梁、杆弹性模量为210 GPa.索无应力长度根据设计最终平衡状态下的索张力及几何形状在制作工厂张拉以后放样得到.

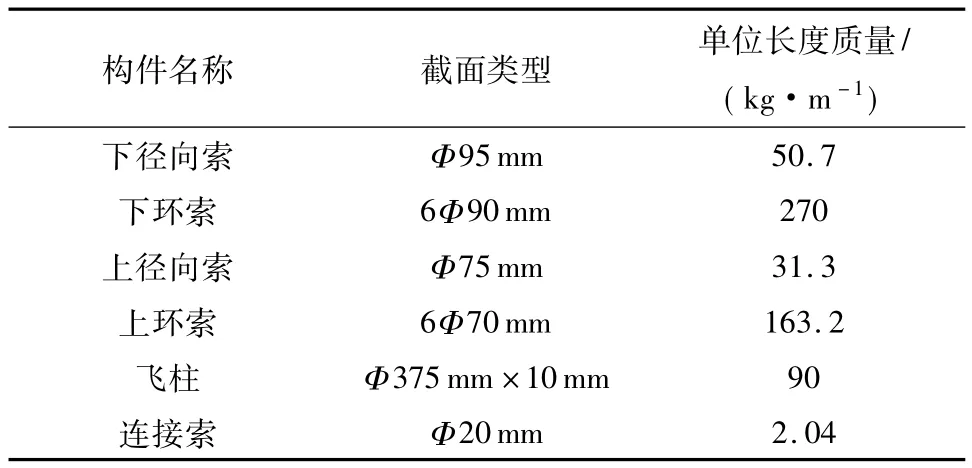
表1 屋盖索杆截面类型Table 1 Cable-strut members of the roof

5.3 计算结果及分析

该工程立柱和环梁截面尺寸和材料属性已知，上、下径向索与环梁的交点按自由节点考虑，即考虑立柱和环梁的变形对屋盖系统成形过程的影响.施工过程状态描述见表2.

索分别采用直线杆单元和抛物线单元进行模拟计算.结构状态由内力和位形两部分组成，在成形过程中，内力主要是索张力，位形主要考虑径向索和环向索交点坐标及环梁节点位移.

图5所示为成形过程中+X轴上、下径向索张力变化过程.图6(a)示出了+X轴上径向索张力差异，图6(b)示出了+X轴下径向索张力差异.从图6可以看出，采用直线杆单元和抛物线单元索的张力相差不大，最大相差3%.尤其是预应力建立起来以后的状态7和状态8，相对变化都不到0.3%，说明预应力建立以后，索单元被充分张拉，索形状已经接近于直线.

表2 张拉成形过程状态描述Table 2 State description of tension forming process

图5 +X轴径向索张力Fig.5 Tension of radial cables along+X axis

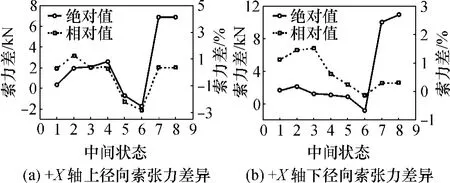
图6 +X轴径向索张力差异Fig.6 Tension difference of radial cables along+X axis

上径向索张力变化可分为3个阶段:从状态1到状态4为第1阶段，该阶段索张力逐渐变大，为上牵引索缩短同时提升下层索的过程;从状态4到状态5为第2阶段，该阶段索张力逐渐变小，是下牵引索缩短同时顶升上层索的过程;从状态5到状态8为第3阶段，该阶段索张力显著增大，为初始预应力和结构刚度建立过程.

同样，下径向索张力也可分为3个阶段:状态1到状态2为第1阶段，该阶段立柱还未安装，为自由悬挂状态，由于环梁产生位移，张力稍有变化;状态2到状态4为第2阶段，该阶段索张力逐渐减小，为上牵引索缩短同时提升下层索的过程;状态4到状态8为第3阶段，该阶段为下牵引索缩短和初始预应力建立过程，该阶段索张力显著增大.

上、下环索节点高程变化见图7(立柱柱底标高为4.899m).抛物线单元最终状态下，+X轴上、下环索节点高程分别为40.058m和22.061m.

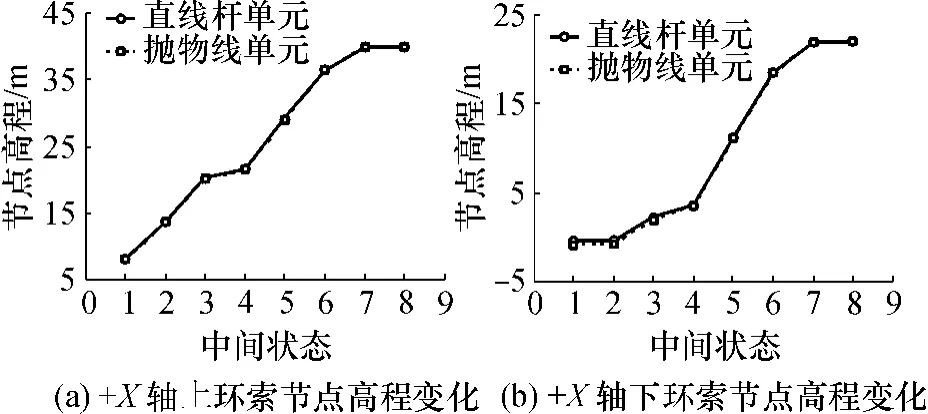
图7 +X环索节点高程变化Fig.7 Height variation of ring cables along+X axis

为清楚表示两种不同索单元对计算结果的影响，图8(a)示出了+X轴上环索节点的直线杆单元z坐标与抛物线单元z坐标之差，图8(b)为+X轴下环索节点z坐标之差.从图8可以看出，索采用不同单元样式对结构平衡形状影响比较大，尤其在预应力建立起来以前，+X轴上、下环索节点高程最大分别相差64.9mm和325.7mm，下环索差值比较大是因为下牵引索长度比较长，这说明索单元越长、索张力越小，直线杆单元误差越大，抛物线单元也就越准确.预应力建立以后，两种不同单元的计算结果差别不大，+X轴上、下环索高程相差均为0.7mm.

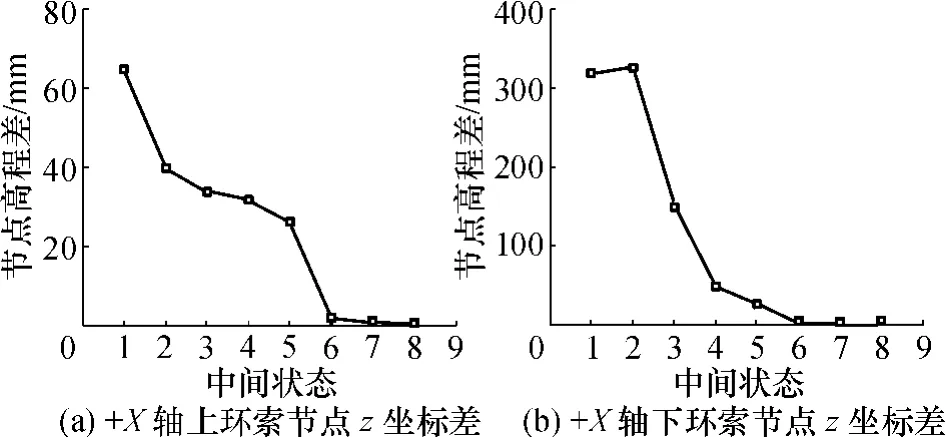
图8 +X轴环索节点z坐标差Fig.8 Nodal z-coordinate difference of ring cables along+X axis

图9 +X和+Y立柱顶点线位移Fig.9 Translational displacement of column top along+X and+Y axes

图9示出了成形过程中周边节点的位移变化过程.在预应力建立前，周边节点位移很小，最大位移都在20mm以内;从状态6开始，节点位移迅速变大;最终状态最大位移发生在+Y轴，达-114.4mm.由于索轴向刚度非常大，周边节点位移将对索张力产生很大影响，所以考虑周边结构变形更接近于实际成形过程.

6 结语

文中采用抛物线单元来模拟索，利用铰接索杆体系平衡矩阵建立节点不平衡力列式;对周边梁、柱、索节点，基于有限元节点平衡方程，考虑连续协调的约束线位移和边界约束，采用静力凝聚法对分块刚度矩阵凝聚缩减，建立周边节点仅考虑三线自由度不平衡力的统一节点不平衡力列式.然后，采用动力松弛法对协同作用整体结构体系的节点不平衡力方程进行非线性迭代求解，并编程实现了该算法.文中提出的算法避免了施工过程中整体刚度矩阵奇异的问题.将文中提出的算法应用到深圳市宝安体育场结构中，通过缩短牵引索模拟结构施工过程.模拟分析表明，文中提出的算法简单有效.通过两种不同单元的比较发现，在成形过程中，特别是预应力建立以前，用抛物线单元来模拟索更准确.分析结果也说明，施工过程中，特别是预应力建立以后，周边结构变形不能忽略，所以考虑周边结构的影响更为恰当.

［1］郭彦林，江磊鑫，田广宇，等.车辐式张拉结构张拉过程模拟分析及张拉方案研究［J］.施工技术，2009，38(3):30-34.Guo Yan-lin，Jiang Lei-xin，Tian Guang-yu，et al.Simulating tensioning analysis and tensioning scheme for wheel tension structure［J］.Construction Technology，2009，38(3):30-34.

［2］完海鹰，黄炳生.大跨空间结构［M］.北京:中国建筑工业出版社，2008:1-20.

［3］江磊鑫，郭彦林，田广宇.索杆结构张拉过程模拟分析方法研究［J］.空间结构，2010，16(1):11-18.Jiang Lei-xin，Guo Yan-lin，Tian Guang-yu.Simulating tensioning analysis for cable-strut tensile structure［J］.Spatial Structures，2010，16(1):11-18.

［4］袁行飞，董石麟.索穹顶结构施工控制反分析［J］.建筑结构学报，2001，22(2):75-79.Yuan Xing-fei，Dong Shi-lin.Inverse analysis of construction process of cable dome［J］.Journal of Building Structures，2001，22(2):75-79.

［5］张其林，罗晓群，杨晖柱.索杆体系的机构运动与弹性变形的混合问题［J］.计算力学学报，2004，21(4):470-474.Zhang Qi-lin，Luo Xiao-qun，Yang Hui-zhu.Mechanism motion and motion-deformation hybrid problems of cablemember systems［J］.Chinese Journal of Computational Mechanics，2004，21(4):470-474.

［6］钱若军，苏波，林智斌.工程结构中的几何位移分析理论、方法和应用研究［J］.工程力学，2008，25(8):70-76.Qian Ruo-jun，Su Bo，Lin Zhi-bin.Study on theory of geometric-displacement analysis，methods and applications in engineering structures［J］.Engineering Mechanics，2008，25(8):70-76.

［7］邓华，姜群峰.环形张力索桁罩棚结构施工过程的形态分析 ［J］.土木工程学报，2005，38(6):1-7.Deng Hua，Jiang Qun-feng.Shape analysis of annular tensile cable-strut canopy structures during erection process［J］.China Civil Engineering Journal，2005，38(6):1-7.

［8］阚远，叶继红.动力松弛法在索穹顶结构形状确定中的应用 ［J］.工程力学，2007，24(9):50-55.Kan Yuan，Ye Ji-hong.Form finding of cable domes by modified dynamic relaxation［J］.Engineering Mechanics，2007，24(9):50-55.

［9］钱若军，杨联屏.张力结构的分析、设计、施工［M］.南京:东南大学出版社，2003:185-190.

［10］Rezaiee-Pajand M，Alamatian J.The dynamic relaxation method using new formulation for fictitious mass and damping ［J］.Structural Engineering and Mechanics，2010，34(1):109-133.

［11］沈世钊，徐崇宝，赵臣.悬索结构设计［M］.北京:中国建筑工业出版社，2002:67-77.

［12］刘树堂.杆系结构有限元分析与MATLAB应用［M］.北京:中国水利水电出版社，2007:227-235.