印制电路板中孔清洗效果分维表征研究

董颖韬 何 为 周国云 王守绪

电子科技大学电子薄膜与集成器件国家重点实验室

徐 缓 覃 新 罗 旭

梅州市博敏电子有限公司

孔壁的清洗质量是影响孔金属化的一个重要因素, 测定并改善孔壁的形貌, 对孔金属化工艺具有重要意义。现在对孔壁清洗质量测试方法主要是通过金相切片观察，并主观定性来判定。这种宏观定性观察的方法，没有深入考虑孔壁表面的微观机制, 这不利于深入研究孔壁形貌对金属化孔质量的影响情况。本文应用分形几何来分析清洗后的孔壁微观形貌，测出材料形貌曲线的分维数, 并将此分维数跟孔金属化的质量优劣联系起来。从微观尺度上，用孔壁的分维数来评价孔壁的清洗质量和孔金属化的影响，从而使微观形貌描述孔的宏观性能和定性的说明转变为定量的分析，为研究孔金属化工艺提供了新思路，对生产指导具有一定的现实意义。

分形是由美国IBM公司研究中心物理部研究员暨哈佛大学数学系教授数学家曼德布罗特1975 年首次提出的,其原义是“不规则的、分数的、支离破碎的”物体, 是没有特征长度的图形、构造以及现象的总称。分形理论是处理极不规则的非线性、非平衡系统的一门有力的数学工具。

分形目前尚无严格的定义，但一般认为分形体应该具有以下几个特征：

（1）具有精细的结构，即有任意小比例的细节；

（2）不规则，无论整体或部分都不能用欧氏几何来描述；

（3）有自相似性，这种自相似性可以是严格的自相似性（称为有规分形），也可以是统计意义上的自相似性（称为无规分形）[1]。

分维是分形结构的度量工具,也就是空间维数是可以连续变化的，它可以是整数也可以是分数，称为豪斯道夫维数；分维可以表示为：

式中：N 为小几何体的数目；r为几何体线尺度所缩小的倍数，即每个几何体的线度是原几何体的1/r；D即为自相似分形维数[2]。分形维数的测试方法有多种：计盒数法[3]、小岛法、垂直截面法[4]、扫描二次电子法等，本文应用计盒数法和垂直截面法来测量孔壁分形维数。

1 实验

1.1 实验样品

选取FR-4无卤双面板（铜厚18 µm/ EP厚0.12 mm /铜厚18 µm），孔径φ＝0.35 mm，为达到较大跨度的分形形貌，用不同的去钻污工艺和参数处理了8组式样作为样品[5]。

1.2 样品的分形判定

本文分维测试的对象是去钻污处理后的孔壁表面形貌的轮廓线，对试样孔做金相贴片，提取二维曲线，图1是一组典型的孔壁形貌图（500倍的金相贴片显微图）。其边缘曲线结构比较复杂，通过放大来看，细微的边缘曲线结构里面仍然含更细微的边缘曲线，而且细小结构跟整体结构非常相似，满足分形的条件，所以该孔壁形貌曲线可看作是分形结构，可以采用分形方法处理。

图1 孔壁分形形貌图

1.3 计算机图形处理

（1）取样：制作孔的金相贴片，并对孔贴片拍照，提取500倍显微图像；

（2）二值化：用photoshop cs2图形处理软件将放大的位图转化为二值化的黑白图；

（3）提取轮廓线：提取上面二值图的轮廓线，将孔壁形貌的垂直截面曲线分离出来，这样才真正得到所需的直接样本，如图2操作过程。

图2 金相切片图形提取过程

由图3可以看出，8组不同形貌的孔壁在平面内的分布都具有明显的非线性特征，只是不同种孔壁分形曲线表现的非线性程度不一样；常规的统计学方法无法描述和评价这类复杂图形，因此可以借助分形理论来对此类图像曲线进行分形分析。

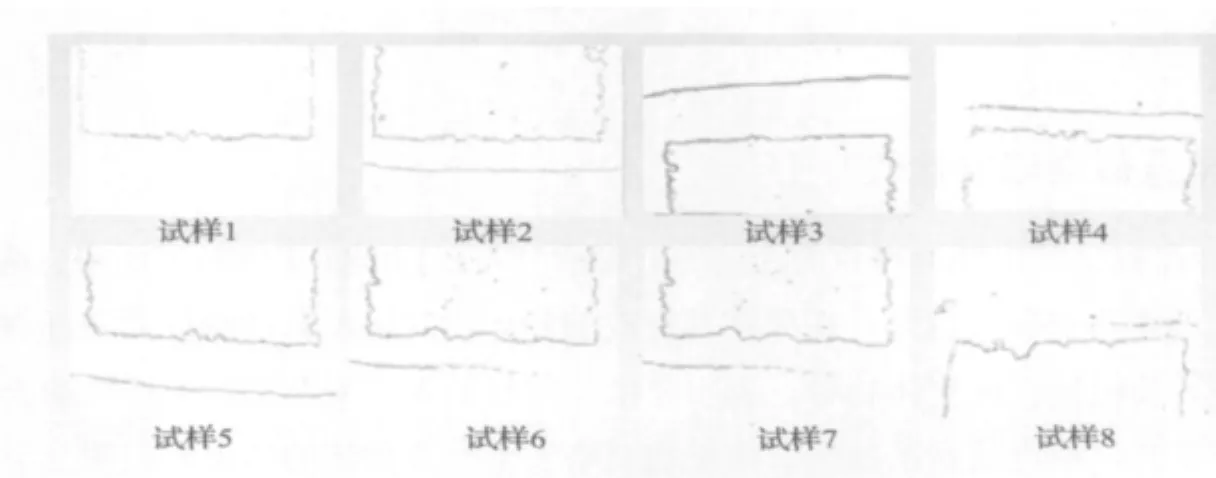
图3 8组典型试样的分形曲线图

1.4 曲线分维值的计算

对一典型式样分别采取计盒数法和垂直截面法计算其分维值（如图4、图5）。

计盒数法：利用photoshop cs2将经过每一组孔壁的分形曲线提取出来，并进行网格覆盖；选取单位长度r分别为2 mm、4 mm、8 mm、16 mm、32 mm、64 mm共六个码尺的网格，分别覆盖分形曲线，数出非空方格N，对N∝r-D，采用Origin 8数据处理软件，通过最小二乘法对[InN(ri)，Inri]作线性拟合，便得到D的估计值。如图4，斜率k-1.0336，则此试样的分维D＝-k＝1.0336；从拟合结果发现，lnN(r)与lnr之间存在很明显的线性拟合关系，R2为0.9963；表明此形貌曲线的整体与局部之间存在相似性，即具有明显的分形特征。

垂直截面法：将经过计算机处理得到的每一类分形曲线分别打印出来，选取单位长度r分别为4 mm、6 mm、8 mm、10 mm、12 mm共5个码尺，分别度量分形曲线的长度了L(r)，由N(r)＝L/r∝r-D，得L∝r1-D。采用Origin 8数据处理软件，通过最小二乘法对[InL(ri)，Inri]作线性拟合，便得到D的估计值。如图5，同一特征分形曲线，采用垂直截面法得到斜率b＝-0.0594，则此试样的分维值D＝1-b＝1.0594，从拟合结果发现，lnL(r)与lnr 之间的线性拟合关系不是很显著，R2为0.4693；表明垂直截面法处理孔壁形貌的分形曲线精确性存在不足。

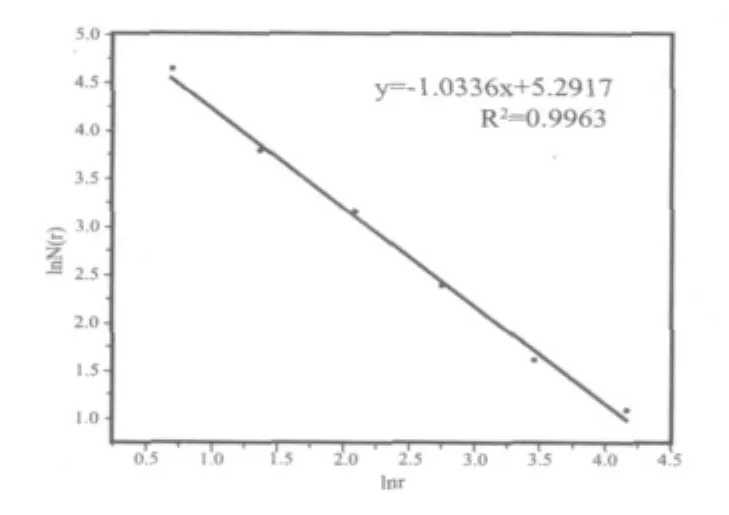
图4 计盒数法的双对数拟合结果

重复上述过程，分别处理8组不同条件去钻污处理的孔的分形维数值，各组试样的分形维数平均值统计结果列于表1。

表1 不同测量方法的各组孔壁分形维值D

2 结果与分析

2.1 计盒数法和垂直截面法的比较

由表1可以看出计盒数法测得FR-4材质的孔壁的分维值分布在1.0085～1.0884，而垂直截面法测得的分维值分布在1.0138～1.1202，两者与实际金像贴片图像及其提取的轮廓线对比，都能很好的表征材料孔壁表面形貌的复杂程度和粗糙度的差异及粗糙程度变化趋势。表明分维能较好的表征复杂的、非线性的去钻污处理的孔壁表面形貌。在处理同一样品时，垂直截面法处理的结果均要略大于计盒数法的结果，表明分形在不同的方法处理下具有一定差别，但都有良好的可参考性。另外计盒数法在计算孔壁分维时，双对数曲线的拟合相关系数均高于0.9，可靠性好；而垂直截面法获取的数据较为离散，双对数曲线拟合程度不高，造成结果误差较大。对可靠性而言，以计盒数法测量结果作为判断去钻无处理的孔壁分形特征更具有实际意义。

2.2 热应力冲击测试

根据IPC-TM-650标准进行热应力冲击试验，浸锡温度288 ℃，浸锡时间10 s，浸锡3次后孔壁状态。由图6可以看出，在孔壁经3次热冲击后孔壁基材与镀层发生分离和破坏[6]。

图6 热应力冲击孔壁效果

对各组试样作金相贴片，分别监测50个孔，其良品占有率如图7。可以看出，在粗糙的孔壁上，尤其是当孔壁有的凹坑时，即使镀层很完整，但在强热冲击后，很容易在凹坑处和边缘发生镀层破坏和剥离（如不良品1）；在光滑的孔壁上，容易获得连续均匀的镀铜层，但附着力较差，强热冲击后容易发生整体镀层剥离（如不良品2）。只有孔壁表面粗糙程度均匀的孔，强热冲击后镀层完整无损[图6（b）]。

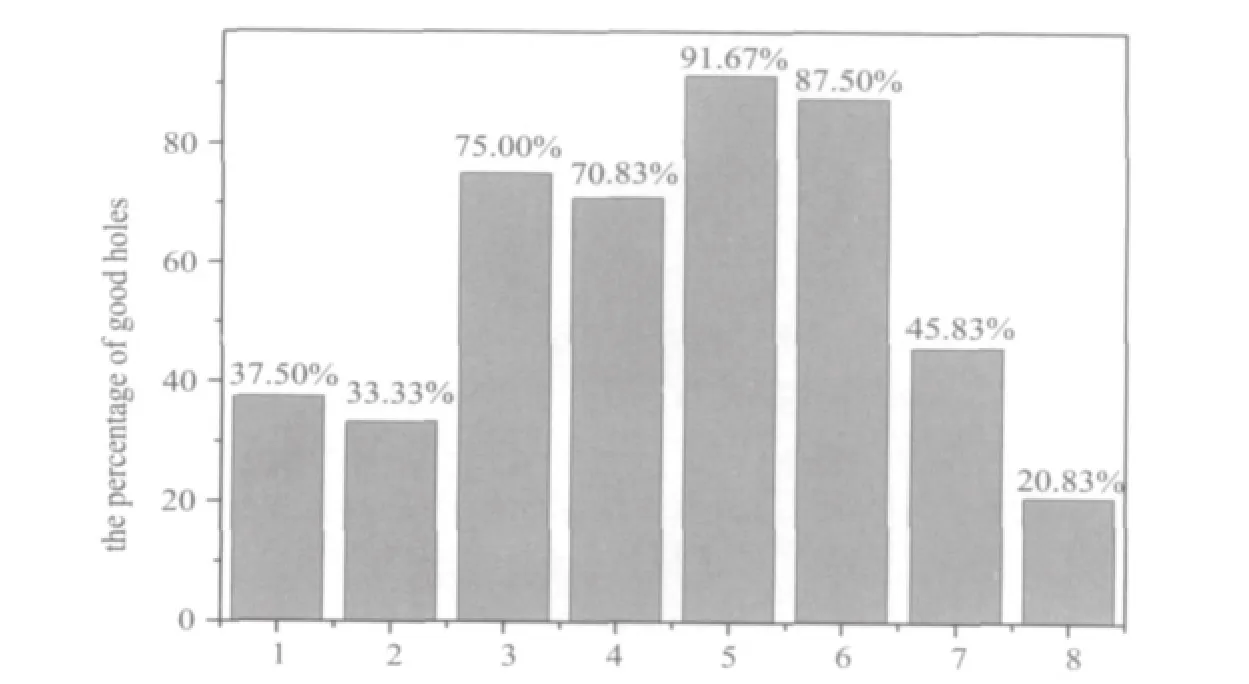
图7 热应力冲击后金属化孔良品率

2.3 孔壁形貌分维与热应力冲击测试结果的关系

热应力冲击测试表明，金属化孔的质量随分维值的增大，先增加，再下降，形成近似抛物线的变化趋势。通过图8可以发现，孔金属化的质量随着孔壁的分形维数的变化而有规律的变化。在计盒数法计算下的清洗后孔壁分维在1.0344时，金属化孔具有最好的可靠性；而垂直截面法在1.0594时具有最好可靠性。两者曲线都呈现先急剧增加，再缓慢变化，再急剧下降的特点，表明粗糙程度越小或越大，它们对孔的好坏都具有决定性影响，是主要的影响因素。

图8 孔壁的分维与热应力冲击测试结果的关系

3 实验结论

（1）对FR-4材质覆铜板，在孔金属化工艺中，清洗后的孔壁形貌具有统计分形特征, 通过经图像处理后可采用计盒数法和垂直截面法测量孔壁的分形维数。

（2）计盒数法测得的分维值分布在1.0085～1.0884，垂直截面法测得的分维值分布在1.0138～1.1202，两者均能对孔清洗效果进行客观的定量表征，可分别作为独立的参考标准。但计盒数法具有操作简单，结果可靠，普适性强等优点，在印制电路板工艺中可得到广泛的实际应用。

（3）热应力冲击效果表明粗糙度均匀的孔具有良好的耐冲击性能，过于光滑和粗糙的孔壁在严酷环境下均不稳定。这样对孔壁的清洗效果就需要达到一种均匀的粗糙面。这种粗糙程度可以定量的用分维来表征。在计盒数法计算下清洗后孔壁分维分布在1.0344附近具有良好的可靠性；而垂直截面法分布在1.0594附近。则可将分维作做为一个定量评价孔壁清洗效果好坏和孔金属化优劣的一个标准。

分维能较好地表征孔壁表面形貌的复杂程度和粗糙程度的差异，突破了传统的仅靠主观观察判断金相切片图形来描述孔壁清洗效果的好坏和金属化孔的优劣。这样的定量的表征有利于严格的控制工艺参数，对印制电路板的制作有实际的指导意义。放眼未来，分形理论一定会在PCB行业的应用越来越广。

[1]Mandelbrot B B.The fractal geometry of nature[M].New York: W H Freeman, 1983.

[2]亢宽盈.分形理论的创立、发展及其科学方法论意义[J].科学管理研究, 1998, 16 (6) : 54-56.

[3]韩杰, 陆桂华.测量分维的矢量计盒算法研究[J].中国图象图形学报, 2008, Vol.13, No.3: 26-30.

[4]易成, 张亮等.一种新的描述粗糙表面形貌尺度分维参数Rd的研究[J].中国矿业大学学报, 2007, Vol.36, No.1:75-80.

[5]张怀武，何为等..印制电路原理与工艺[M].北京:机械工业出版社, 2009,

[6]吴云鹏.印制板孔金属化的影响因素及改善[C].2009春季国际PCB技术/信息论坛论文集, 2009.