考虑氯离子侵蚀的钢筋混凝土桥梁疲劳时变可靠度

张丽华，贾金青，余 芳

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

钢筋混凝土桥梁结构常常会在低于材料的强度极限或屈服极限的反复荷载的作用下发生突然的疲劳破坏。其服役过程中腐蚀介质引起的钢筋锈蚀不仅减小钢筋有效截面和增大钢筋疲劳应力幅，同时降低钢筋疲劳强度，严重地影响结构使用寿命。曹建安等［1］在实际桥梁退换下的老化构件中截取锈蚀钢筋进行疲劳强度试验。结果表明，锈蚀不仅使钢筋有效截面、屈服强度和变形能力减小，而且明显降低其疲劳强度。金伟良等［2］的调查结果表明，沿海地区氯离子侵蚀造成钢筋混凝土结构中钢筋锈蚀十分严重，锈蚀速度远高于碳化引起的钢筋锈蚀。因此，在桥梁结构老龄化以及交通流量日益增加、车载增大、使用环境逐渐恶化的情况下，计算氯离子腐蚀环境下钢筋混凝土桥梁疲劳时变可靠指标具有重要意义。

实际工程中，桥梁结构的材料强度及结构上作用的荷载都具有随机性，并且反复荷载作用下结构是否发生疲劳破坏是不确定的，因此应该采用可靠度理论分析疲劳过程。由于服役过程中抗力随时间衰减，结构的失效概率随时间变化，其疲劳可靠度具有时变性。贡金鑫等［3］对腐蚀环境下钢筋混凝土构件的疲劳可靠度分析方法进行了研究，提出考虑疲劳性能降低的结构疲劳可靠度计算方法。

从现有钢筋混凝土梁的疲劳腐蚀试验和工程实例来看［4］，几乎所有破坏均以受拉钢筋突然断裂为破坏标志。据此，氯离子腐蚀环境下钢筋混凝土梁的疲劳计算应作如下假设:不考虑混凝土的疲劳影响，以钢筋疲劳破坏作为钢筋混凝土梁的疲劳计算依据。本文针对氯离子腐蚀环境中的钢筋混凝土桥梁结构的疲劳破坏问题，考虑钢筋的截面特性时变和疲劳强度时变，运用线性累积损伤法则和蒙特卡罗方法，对钢筋混凝土桥梁进行疲劳可靠度分析，计算结构的时变疲劳可靠指标。

1 疲劳抗力衰减

由于钢筋锈蚀是腐蚀环境中钢筋混凝土结构的主要病害，其中氯离子侵蚀环境下钢筋锈蚀包括由氯离子侵蚀导致的均匀锈蚀和裂缝处局部不均匀锈坑，前者主要减小钢筋有效截面，后者则主要降低钢筋材料本身的疲劳性能。因此，钢筋混凝土桥梁构件疲劳性能衰减的关键因素是有效钢筋截面和钢筋疲劳强度。

1.1 钢筋截面锈蚀率

尽管氯离子在混凝土结构中的传输机理很复杂，但扩散被认为是一个主要的传输方式。这个过程一般采用Fick第二定律描述氯离子的扩散浓度、扩散系数与扩散时间的关系，认为混凝土中的孔隙均匀分布，氯离子在混凝土中扩散是一维扩散行为，浓度梯度仅沿着暴露表面到钢筋表面的方向变化。由于混凝土表面氯离子质量浓度与解冻盐饱和溶液的氯离子浓度保持平衡，假定Ccr为钢筋开始锈蚀的临界氯离子浓度值，d为混凝土保护层厚度，则钢筋开始锈蚀时间Tcor为:

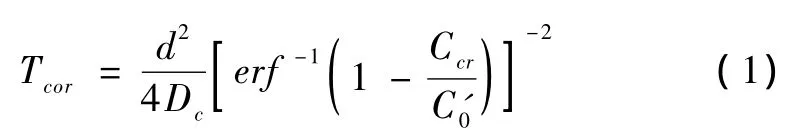
其中，C'0为平衡后的混凝土表面氯离子质量浓度，Dc为氯离子扩散系数，误差函数erf为

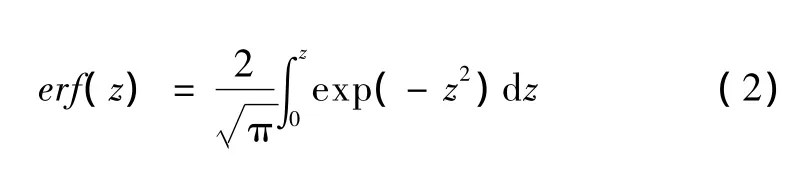
式中，z为氯离子渗透深度。

根据KIM等人研究结果，计算时选取Dc的平均值为 2.0 ×10－8cm2/s，C'0的平均值为 3.5 kg/m3，Ccr的平均值为0.9 kg/m3，则可以算出构件中钢筋开始锈蚀的时间。

通常腐蚀环境中的钢筋有效截面减小仅考虑钢筋整个外露表面的均匀锈蚀。通过非破坏性试验中所采用的参数，锈蚀电流密度 icorr(μA/cm2)，根据法拉第定律:当产生单位锈蚀电流密度即icorr=1 μA/cm2时，相应钢筋的平均锈蚀速度 λ为0.011 6 mm/年［5］。因此，钢筋开始锈蚀后，t时刻钢筋直径D(t)计算公式为

其中，t以年为单位;D0为钢筋初始直径(mm)。

关于锈蚀电流密度icorr，目前国际上一般认为低速锈蚀时icorr服从［2.0，3.0］均匀分布，中速锈蚀时服从［3.0，4.0］均匀分布，高速锈蚀时服从［4.0，5.0］均匀分布。正常情况钢筋为低速锈蚀，因此，本文假设icorr不随时间变化［7-8］，取 icorr=2.0 μA/cm2，则有

其中，λ=0.023 2icorr

钢筋直径减小导致钢筋的截面积As减小，由此引起的钢筋锈蚀率 (即截面损失率)ηs计算式为

其中，n为钢筋根数;Di(t)为第i根钢筋t时刻直径。

1.2 锈蚀钢筋疲劳性能

通常情况下，材料疲劳极限强度与疲劳循环次数的关系可以用S-N函数表示为［3］

其中，Δσ为材料的应力变程;N为应力变程Δσ下，材料可经受的应力循环次数;m和C为材料的疲劳性能常数。如果不考虑材料的疲劳性能变化，对于确定的目标疲劳次数N，可由S-N函数得到钢筋的疲劳极限强度 Δσ。

由于氯离子腐蚀环境中，钢筋锈蚀率不断增大，局部锈坑的产生使钢筋表面结构变化，产生应力集中。这时在疲劳荷载作用下会加速腐蚀介质的渗透，加剧钢筋损伤，降低钢筋抗疲劳性能，所以服役期内必须考虑材料疲劳强度时变。同时结构疲劳分析时，常使用对数形式表示材料的高周期疲劳段函数，则采用随机过程反应疲劳性能随时间变化的疲劳函数对数表达式为

其中，C0为规定的疲劳循环次数(常取2×106次)对应钢筋试件的疲劳性能常数，函数m(t)，φ(t)为反映结构服役过程中材料疲劳性能降低的系数。由于m的变异性很小，本文将其视为确定值;函数 φ(t)有待通过试验和工程调查确定。

根据不同锈蚀状态下的钢筋疲劳性能劣化规律试验，通过分析试验数据可以得出锈坑深度和钢筋疲劳强度系数降低关系［6］，从疲劳荷载循环次数N的下降来研究参数C的劣化规律，建立钢筋疲劳强度系数φ(t)的时变模型

式中，Δδ(t)为钢筋锈蚀深度，可通过钢筋直径变化函数计算。

2 时变疲劳可靠度

2.1 疲劳应力分析

在设计基准期内，桥梁结构的疲劳应力变化的时间历程是由实际运行状态下疲劳荷载产生的，实际作用在桥梁构件上的疲劳荷载可通过调查统计得到。由于疲劳荷载的大小、作用时间具有随机性，因此荷载也采用随机过程进行分析。公路桥梁结构中主要产生疲劳荷载效应的是车辆荷载，根据交通部“公路桥梁车辆荷载研究”课题组的研究，车辆荷载随机过程可用泊松过程或伽马过程来模拟［7］。本文假定桥梁结构设计基准期内的反复荷载作用为泊松随机过程。设计基准期内，活载作用阶段的变化次数服从泊松分布。

基准期内［ti－1，ti］时段活荷载在构件上作用弯矩幅 ΔMQi引起钢筋应力变幅［8］:

其中，αEi，h0i，xi，I0i分别表示此时段钢筋弹性模量和混凝土疲劳变形模量的比值，截面有效高度，受压区高度和换算截面惯性矩。

由于钢筋有效截面时变直接表现为钢筋截面面积AQi减小，所以用如下方法计算钢筋应力ΔσQi为

计算时，忽略钢筋有效截面减小对钢筋内力偶臂长度Zi的影响，此时可方便地求出构件上活载弯矩作用下由钢筋截面面积减小引起的钢筋应力变程。

2.2 疲劳累积损伤

结构疲劳可靠度的三种分析模式分别为疲劳极限应力模式、疲劳极限损伤模式和疲劳寿命模式。由于钢筋锈蚀是一个随时间变化的渐变过程，并且服役过程中钢筋混凝土构件承受随时间变化的荷载作用，因此本文选择疲劳极限损伤模式计算构件的时变可靠度。

当结构承受变幅循环应力作用时(图1所示)，第i组循环应力的应力幅为 Δσi，循环次数为 ni，总循环次数因此根据 Miner线性累积损伤法则，应力循环ne次后结构的累积疲劳损伤系数D'为

图1 变幅循环应力示意

对工程中常见的随机疲劳荷载，如果应力变程的概率密度函数为 fΔσ(Δσ)，则高周疲劳破坏时，ne足够大，式(11)进一步表示为

在设计基准期内，考虑腐蚀环境中钢筋有效截面和疲劳性能降低，［ti－1，ti］时段内应力循环 ni次后采用极限累积损伤模式分析的累积损伤Dj为

其中，Δσj为［ti－1，ti］时段钢筋疲劳应力幅，φ(t'i)是 φ(t)离散后t'i时刻函数值，反映此时段钢筋疲劳性能的衰减。

因此，设计基准期内构件的线性累积损伤系数D'为

2.3 疲劳失效概率

采用线性累积损伤法则计算的疲劳损伤系数D'并不总是等于1，而与应力循环次序有关。根据国内外研究结果［9］，将疲劳破坏的失效概率Pf表示为

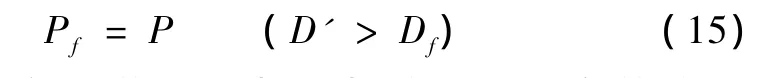
其中，P为概率函数;Df为随机变量，平均值介于0.836～1.720之间，变异系数 δ介于0.161～0.980之间。通常，应力变程逐步增大时，Df＞1;应力变程逐步减小时，Df＜1。

3 计算实例

图2所示为一T形截面钢筋混凝土公路桥梁。梁的计算跨度为15 m。采用C25混凝土，梁底配有10根Ⅱ级钢筋，其中8根直径为32 mm，2根直径为20 mm。钢筋混凝土保护层厚度为30 mm。

图2 T梁横断面(单位:mm)

按公路工程技术标准［10］，活荷载服从极值Ⅰ型分布，考虑冲击系数影响，在梁跨中截面产生疲劳弯矩SQ平均值 μSQ=505.97 kN·m，变异系数 δSQ=0.086 2。根据钢筋疲劳试验结果［11］，取梁内钢筋的疲劳S-N方程(Δσ)mN=C0，其中疲劳性能参数 m=4.382 7，C0服从对数正态分布，平均值 μC0=1.37×1015，变异系数δC0=0.4。

由式(1)计算钢筋初始锈蚀时间 Tcor为5.5年，结构设计基准期内，氯离子侵蚀作用引起的随时间变化的钢筋截面锈蚀率由式(5)计算。同时可以计算出钢筋锈蚀量时变函数，从而得到钢筋疲劳强度时变系数φ(t)，见图 3。

由于几乎所有的钢筋混凝土梁结构疲劳破坏均以受拉钢筋疲劳破坏为标志，所以计算腐蚀环境下钢筋混凝土桥梁疲劳可靠度时，以钢筋疲劳破坏作为疲劳计算依据。同时为了简化计算，Df作为确定量取值为1。可靠指标计算时采用 Monte-Carlo方法［12］，借助Matlab软件编制程序，分别计算考虑钢筋有效截面时变和疲劳性能衰减情况下，设计基准期内结构疲劳累积损伤随使用时间变化的可靠度指标，结果见图4。

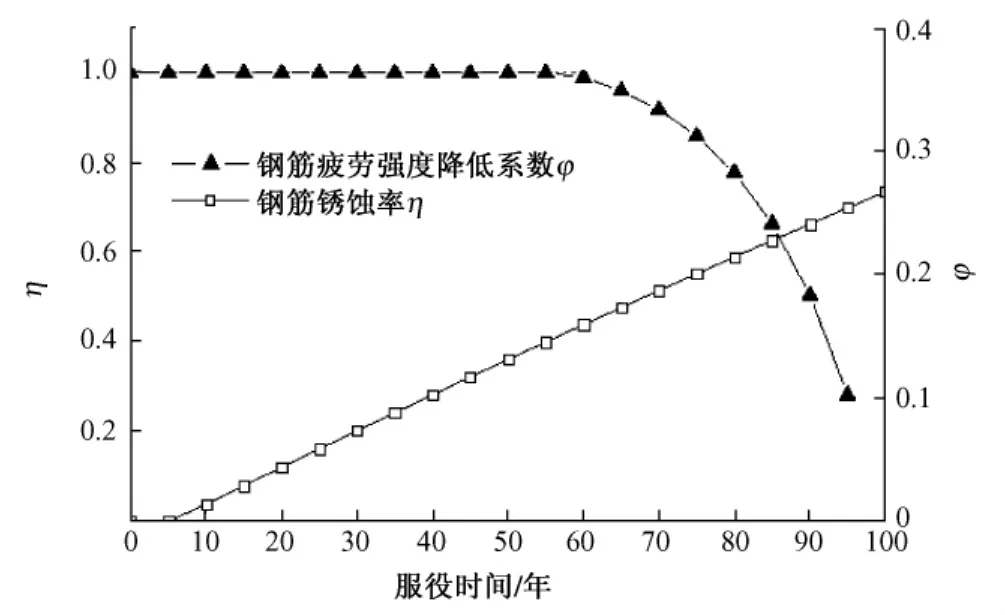
图3 钢筋锈蚀率及疲劳强度降低系数曲线

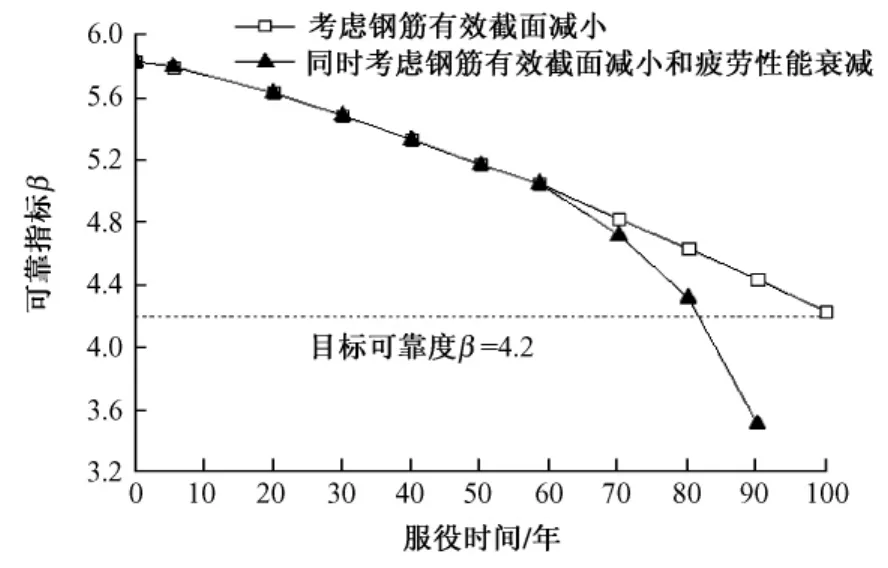
图4 时变疲劳可靠度指标曲线

结果表明:氯离子侵蚀引起的钢筋有效截面减小会降低桥梁疲劳可靠指标;在钢筋出现局部锈坑后，由于钢筋疲劳强度发生衰减，氯离子侵蚀对桥梁的疲劳可靠指标有更显著的降低作用。

通过上述计算可知，氯离子侵蚀作用下该桥服役5.5年后钢筋锈蚀，导致疲劳可靠度降低速度增加，此时应对桥梁进行维修检测，采取有效保护措施，控制钢筋锈蚀;同时考虑钢筋有效面积减小和钢筋疲劳性能衰减的情况下，结构服役超过80年时桥梁的疲劳可靠指标小于目标值4.2，失效概率高于可接受水平，此时必须采取维修措施，对桥梁结构进行加固或改造，以保证桥梁结构满足安全性要求。

4 结论

1)基于混凝土中氯离子扩散及其引起的钢筋锈蚀的机理，提出了钢筋面积随时间变化的公式。并结合钢筋疲劳强度时变模型，运用线性累积损伤法则和蒙特卡罗方法，对钢筋混凝土桥梁进行疲劳可靠度分析，计算了桥梁结构时变疲劳可靠指标。计算结果表明，氯离子侵蚀作用下钢筋有效截面减小和疲劳性能衰减显著降低桥梁结构的疲劳可靠指标。

2)本文建立的计算模型，可用于对氯离子侵蚀环境中钢筋混凝土桥梁服役期内的疲劳可靠度分析，计算能够对结构的可靠性进行动态的评估，为结构的可靠性鉴定、耐久性评估以及结构构件的维修决策提供参考。

［1］曹建安，文雨松．锈蚀钢筋的疲劳试验研究［J］．长沙铁道学院学报，1998，16(4):15-18.

［2］金伟良，张苑竹．浙东沿海高桩码头耐久性调查与对策［C］//混凝土结构耐久性及耐久性设计会议文集．北京:清华大学，2002.

［3］贡金鑫，赵国藩．腐蚀环境下钢筋混凝土结构疲劳可靠度的分析方法［J］．土木工程学报，2000(6):50-56．

［4］李鹏．腐蚀环境下钢筋混凝土结构疲劳性能研究［D］．长沙:中南大学，2009．

［5］STEWART M G，MELCHERS R E．Reliability of deteriorating RC slab bridges［J］．Structure Engineering，1997，123(12):1638-1644.

［6］彭修宁．锈损后钢筋混凝土疲劳耐久性若干问题的研究［D］．南宁:广西大学，2004.

［7］中华人民共和国交通部．GB/T 50283—1999 公路工程结构可靠度设计统一标准［S］．北京:中国计划出版社，1999．

［8］中华人民共和国建设部．GB 50010—2002 混凝土结构设计规范［S］．北京:中国建筑工业出版社，2002.

［9］李永强，车惠民．混凝土弯曲疲劳累积损伤性能研究［J］．中国铁道科学，1998，19(4):52-59．

［10］中华人民共和国交通部．JTG B01—2003 公路工程技术标准［S］．北京:人民交通出版社，2003.

［11］曾志斌，李之榕．普通混凝土梁用钢筋的疲劳 S—N曲线研究［J］．土木工程学报，1999，32(5):10-14.

［12］赵国藩．工程结构可靠性理论与应用［M］．大连:大连理工大学出版社，1996．