非线性函数法研究曲率对弯箱梁桥的影响

宋国华，霍 达，罗 玲，3，王东炜

(1.郑州大学 土木工程学院，湖南 郑州 450001;2.北京工业大学 建筑工程学院，北京 100022;3.北京市市政工程设计研究总院，北京 100045)

弯桥和直桥相比，最大的不同点主要在于曲率所引起的弯扭作用的耦合。一般而言，这种弯扭联合作用，随着曲率和桥宽的减小而减小。

研究表明，圆心角、曲率半径、弧长、桥面宽度以及弯扭刚度比等，是区分曲梁、直梁受力特征的主要因素［1］。除了影响直线桥受力特性的因素，如跨长、抗弯刚度外，与弯桥有关的主要因素还有圆心角。主梁的弯曲程度是影响弯桥受力特性最重要的因素，能全面反映主梁弯曲程度的参数是圆心角，它是跨长与半径的比值，反映了与跨径有关的相对弯曲关系。如果桥梁跨长一定，主梁圆心角的大小就代表了梁的曲率，圆心角越大，曲率半径就越小，所显示的弯桥的受力特点就越明显［2］。

本文主要研究桥长L和圆心角φ对二等跨连续弯箱梁桥的结构反应的影响。提出以梁格系法为理论基础编制的“斜弯坡及异形空间分析软件系统3DBSA”为结构计算分析工具，以 Matlab为数据处理工具，用非线性函数法建立变截面两跨弯箱梁桥受力性能与圆心角及桥长间的显示函数关系。

1 模型建立

研究参数有圆心角 φ、桥长L，它们的取值范围如下:

1)φ:30°，60°，90°，120°，150°。

2)L:50，70，80，100，130，150 m。

这样共建立6×6=36个模型。

1.1 截面特性

选用单箱单室截面，上宽9．0 m，下宽5.0 m，两翼板宽度各为2.0 m，顶板厚0.20 m，底板厚0.35 m，两侧上翼缘板根部厚0.30 m，端部厚0.15 m，直线过渡。桥梁跨中高度取为单跨长的1/40，支座高度取为单跨长的1/18，其它截面高按二次插值生成。各模型的支座截面高度和跨中截面高度的取值见表1。图1、图2分别列出了圆心角 φ=90°，桥长 L=130 m模型的支座截面和跨中截面。

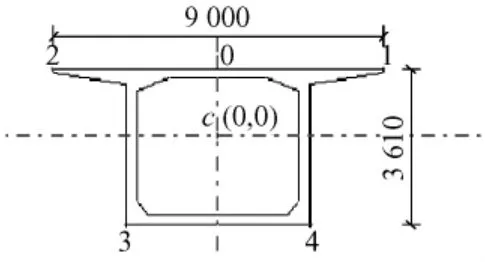
图1 支座截面(单位:mm)

1．2 收缩徐变

按文献［3］规定，取混凝土加载龄期τ=10 d。各模型的收缩徐变参数的取值见表1。

图2 跨中截面(单位:mm)

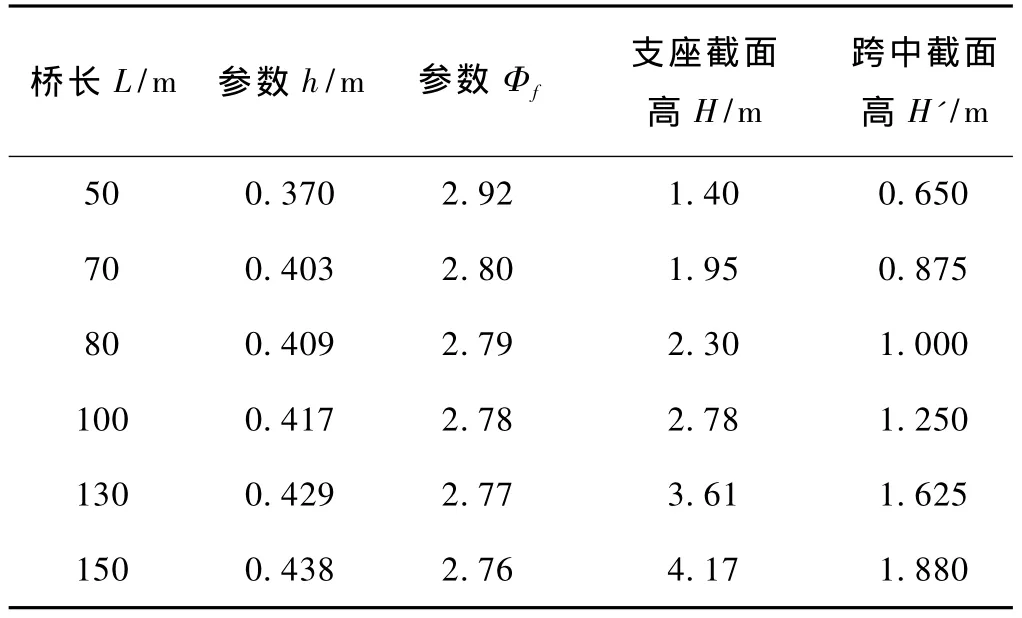
表1 收缩徐变参数及截面高度

1.3 活载

取汽车—超 20级，挂车—120，人群荷载为 3.5 kN/m2，纵向加载步长 1.0 m，横向加载步长 0.5 m。左右车道数均为1，单列系数1，行车时速80 km/h。

1.4 荷载组合

按规范规定取正常使用极限状态和承载能力极限状态下的荷载组合，共有8种。模型建立其它相关内容参见文献［4］。图3为圆心角 φ=90°，桥长 L=130 m的模型在施工阶段4，即收缩徐变完成后的结构分析简化模型。

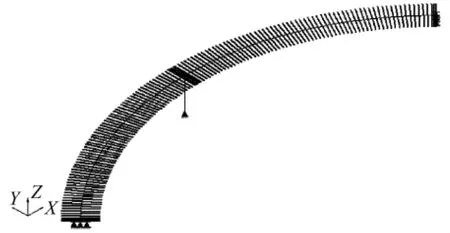
图3 结构分析简化模型

1.5 模型计算

包括4部分:数据处理，施工计算，活载计算及荷载组合。由软件3D-BSA计算。

所关心的结构反应包括分别在正常使用极限状态和承载能力极限状态下控制截面的内力和局部坐标系下自重作用的位移，以及组合1和组合2工况下支承单元的反力。因为上述内力为截面的配筋内力，上述位移最能反映结构变形受参数的影响情况，而支承反力反映了支承本身受φ，L两个参数影响的变化情况。

2 非线性函数法数据处理

Matlab中的函数lsqnonlin()是一个可以方便地拟合出多变量公式的函数，它解决的是非线性最小二乘问题，包括非线性数据拟合问题。lsqnonlin()要求用作者定义的函数来求解向量定义的函数。x=lsqnonlin(fun，x0)以输入初始点 x0开始，求出 fun中所列函数的平方和的最小值。fun返回的是这些值所组成的向量{x}。本文拟合的数值是各种桥梁结构反应，包括内力、位移和支座反力。

该方法的优点是:可以拟合多变量公式，并能整体考虑所有变量的影响。缺点是:需要提前预设所需拟合公式的形式并输入各变量的初始点。另外，如果变量较多，拟合效果不够理想时，需多次调整初始变量值，以达到能满足要求的较优点(极值点)，这是一个优化的过程。本文所确定的拟合标准，是拟合值与原值相差不超过10%。

本文拟合出的结构反应与桥长及圆心角之间的函数关系为:x1φx2Lx3+x4，见表 2。通过分析 x1，x2，x3和x4之间的符号变化就可以确定结构反应与桥长及圆心角的增减关系。分析后可以发现:

1)当x2=0或x2≈0时，不受圆心角影响，或影响很小，可忽略不计。

2)当x3=0时，不受桥长影响。

3)当x1x2＞0时，随圆心角的增大而增大。如x3＞0，则增大程度随桥长的增大而增大;如x3＜0，则增大程度随桥长的增大而减小。

4)当x1x2＜0时，随圆心角的增大而减小。如x3＞0，则减小程度随桥长的增大而增大;如x3＜0，则减小程度随桥长的增大而减小。

5)当x1x3＞0时，随桥长的增大而增大;如 x2＞0，则增大程度随圆心角的增大而增大;如x2＜0，则增大程度随圆心角的增大而减小。

6)当x1x3＜0时，随桥长的增大而减小。如 x2＞0，则减小程度随圆心角的增大而增大;如 x2＜0，则减小程度随圆心角的增大而减小。

将符合以上条件的反应项目列于表3。

下面分析所拟合结果的可靠性，通过对Qymax(承)的拟合值与原值之差相对于原值的比值作一例子，比值结果见表4。

由表4可知，比值结果均在10%以内，说明用非线性函数法拟合弯箱梁桥结构反应与圆心角及桥长的关系还是可行的，结果也比较可靠。

通过以上分析可得如下结论:

1)所有结构反应均受到桥长的影响，不可忽略。

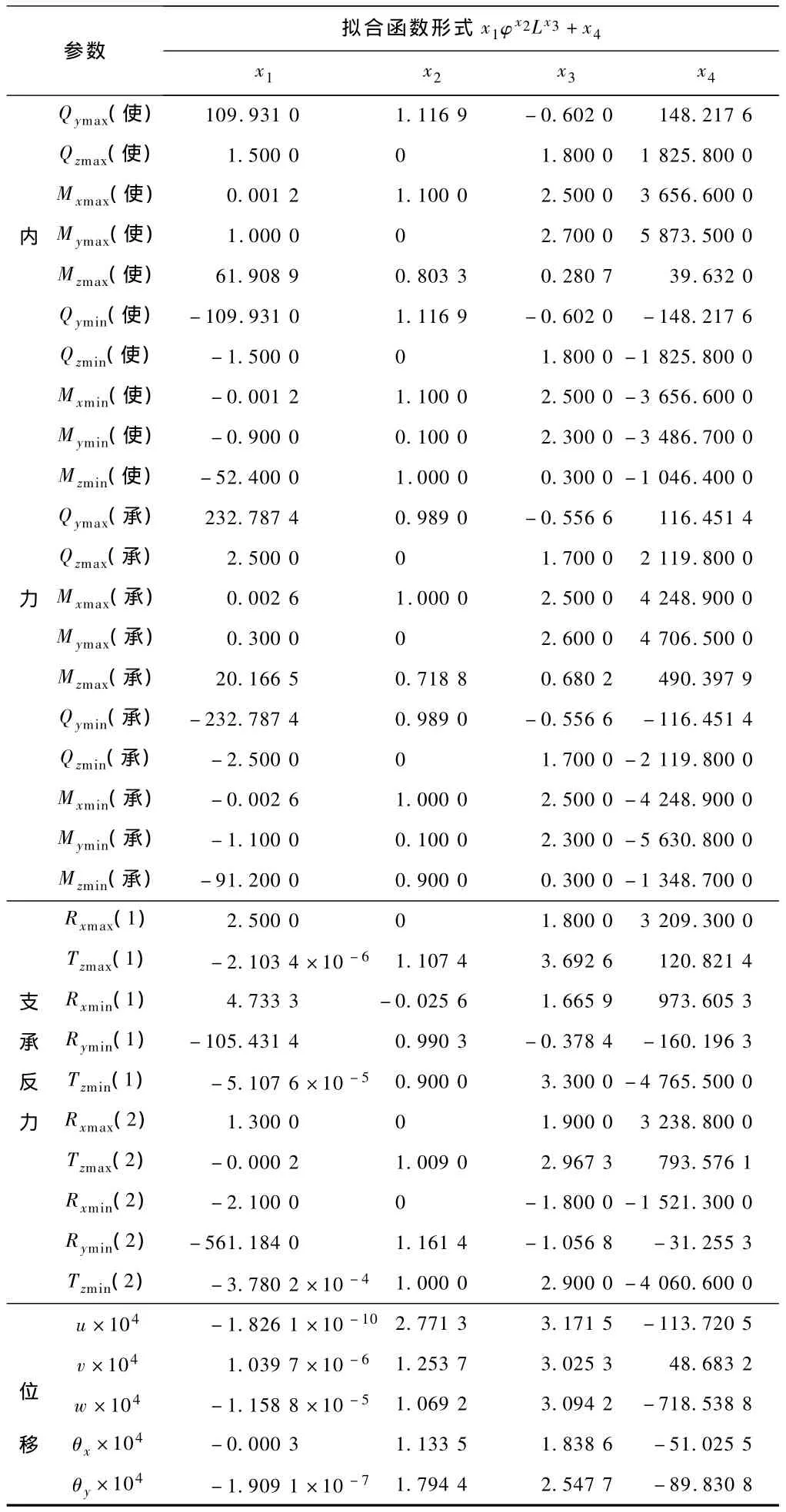
表2 结构反应与桥长及圆心角的拟合函数关系力:kN;位移:m

2)在直梁桥设计计算中存在的主要内力，如Qz，My以及支承反力Rx受圆心角φ影响很小，在弯桥设计中可以不考虑圆心角的影响，而取桥梁中心线长度为跨长来计算弯桥中的内力Qz，My及反力Rx。

3)因曲率存在而使弯桥中产生的附加内力，如Qy，Mx，Mz，支承反力 Ry，Tz及各项位移受圆心角 φ 影响较大，设计时必须考虑圆心角的影响。

表3 各种结构反应受圆心角及桥长影响的分类

表4 Qymax(承)的拟合值与原值之差相对于原值的比值

4)内力 Nx、位移 θz及支承反力 Rymax绝对值均很小，可忽略不计。

3 结论

1)通过统计分析和数值模拟的方法拟合出桥梁结构反应与圆心角及桥长间的显示函数关系，方法可行，结果可靠。

2)用非线性函数法拟合的桥梁结构反应，可以用其变量间的符号关系表达出结构反应受变量影响的增减性。

［1］邵荣光，夏淦．混凝土弯梁桥［M］．北京:人民交通出版社，1994．

［2］CHAN T H T，YUNG T H．A theoretical study of force identification using prestressed concrete bridges［J］．Engineering Structures，2000(23):1529-1537．

［3］中华人民共和国交通部．JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范［S］．北京:人民交通出版社，2004．

［4］宋国华，罗玲，王东炜．偏心支承对120°圆心角双跨弯箱梁桥的影响［J］．桥梁建设，2005(4):44-47．