对桥梁墩顶抗推刚度的思考

赵德强 刘美玲 孙小艳

1 截面刚度与桥梁下部计算时需用到的墩台抗刚推刚度的区别

刚度是构件承受外力作用时抵抗外力变形的能力。说起刚度，我们自然的想起构件在承受拉伸(轴向力N)、扭转(扭矩T)、弯曲(弯矩M)时所用到的刚度:拉伸时的抗拉(压)刚度EA、扭转时的抗扭刚度GIP、弯曲时的抗弯刚度EI。轴向应变而易见，单位变形等于作用力除以刚度。刚度EA，GIP，EI为构件的截面刚度，同一构件上的不同截面(随着截面几何形状的改变)刚度不一定相同。比如由支点的实心截面过渡到跨中的空心截面，在过渡段中截面的刚度是不断变化的。而桥梁下部计算时所需用到的墩台抗推刚度，是针对整个墩台而言的，包括地基基础。对于刚度，现在研究的对象是由“构件截面”改变为“整个结构”。对于给定的一个桥墩包括地基基础，该墩顶的抗推刚度是唯一的。简单的说墩顶抗推刚度的计算模式就相当于一端固定、一端自由的悬臂柱子(柱顶为自由端)，在柱顶发生单位水平位移时，所需的柱顶水平力的大小，即为墩顶抗推刚度值，也即柱顶单位水平力所引起的柱顶水平位移的倒数。

桥梁上部结构主要承受恒载、活载、温度和汽车制动力作用。这些作用都无一例外的由上部结构传至下部结构再传给地基。上部恒载、活载主要转化为竖向力和弯矩作用于墩顶;温度变化(包括收缩徐变)引起上部结构(梁)的伸缩，必带动墩顶发生水平位移，显而易见，该水平位移值乘以墩顶抗推刚度(严格的讲应该是集成刚度:支座刚度与墩顶抗推刚度的集成刚度)，即为由温度变化(包括收缩徐变)引起的作用于墩顶的水平力值;汽车制动力为纵向水平力，引起各墩顶发生大致相同的水平位移，所以汽车制动力按墩顶抗推刚度(严格的讲是集成刚度)分配。墩顶抗推刚度的“顶”字是必不可少的。

墩顶集成刚度计算详见参考文献［1］。

2 墩台顶抗推刚度的简单推导

1)一端固定(墩底)、一端自由(墩顶)的等截面柱，结构力学计算图示如图1所示，即墩底(桩顶)与地面或冲刷线平齐时墩顶抗推刚度的计算，墩身截面全长不变，墩身抗弯刚度恒为EI。利用图乘法:

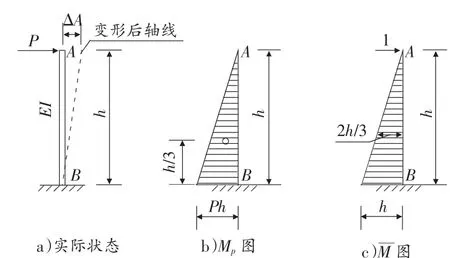
图1 一端固定、一端自由的等截面柱结构力学图

2)一端固定(墩底)、一端自由(墩顶)的等截面柱，材料力学计算图示如图2所示，根据梁的挠曲线近似微分方程:EIv″=-M(x)=Ph-Px，积分两次，再根据变形相容条件，当x=0时，转角v'和挠度v都等于0，可得挠曲线方程当x=h时，可得自由端挠度P=1时同样可得墩顶抗推刚度

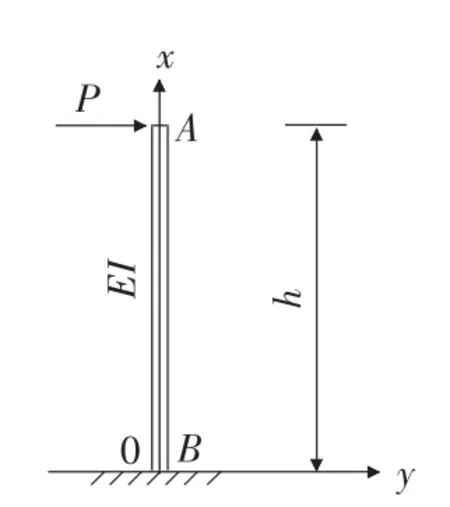
图2 一端固定、一端自由的等截面柱材料力学图

墩顶的刚推刚度是由墩身截面抗弯刚度EI和墩高h组成的一个表达式。结构力学和材料力学该两种计算方法都忽略了剪力和轴向力的影响，一般情况下墩高比墩身截面大好多，不影响精度。两种计算方法殊途同归。

墩底(桩顶)在地面或冲刷线平齐处并非完全嵌固，当在墩顶受到P=1作用时，则桩顶受到P=1，M=P×h=h和竖向力N(竖向力N不影响墩顶抗推刚度的计算，在这里忽略)的作用，桩土需要协调变形，则桩顶必产生变形。根据《公路桥涵地基与基础设计规范》可计算出当单位水平力作用在桩顶时，桩顶处产生的水平位移和转角当单位弯矩作用在桩顶时，桩顶处产生水平位移和转角。而此时桩顶受到P=1，M=h作用，根据叠加原理桩顶水平位移h，转角h，到墩顶就为h2。另外当墩底当成嵌固处理时，墩顶受到P=1作用时，x墩顶1=上可知墩顶受到P=1作用，而且考虑土中桩的变形影响时，墩顶总的水平位移顶抗推刚度

3)一端固定(墩底)、一端自由(墩顶)的不等截面柱，结构力学计算图示如图3所示，即桩顶高于地面或冲刷线时墩顶抗推刚度的计算，设墩身抗弯刚度为E1I1，桩身抗弯刚度为E2I2。

图3 一端固定、一端自由不等截面柱结构力学图式

由图乘法得(见图3):

3 单薄壁墩与双薄壁墩抗推刚度的比较

设单薄壁墩的截面尺寸为B×2H，双薄壁墩其中一个薄壁的截面尺寸为B×2H，墩高均为h，这样两种情况材料用量相等。对单薄壁墩，其顺桥向墩顶抗推刚度为:

对于双薄壁墩其顺桥向抗推刚度为:

由以上两式计算结果可知单薄壁墩的墩顶抗推刚度是双薄壁墩的4倍，因此采用双薄壁墩不仅可以削减墩顶负弯矩峰值，而且因其抗推刚度小，可以有效地减小梁体水平位移(由于温度变化和混凝土收缩徐变等引起的)对墩身的影响。另外双薄壁墩抗弯扭性能也比单薄壁墩强。

以上就是笔者对桥梁墩台顶抗推刚度的一些简单思考，希望能与初学者共勉。

［1］ 袁伦一．连续桥面简支梁桥墩台计算实例［M］．北京:人民交通出版社，1998．

［2］ 姚玲森．桥梁工程［M］．北京:人民交通出版社，2008．