电磁无心夹具定位面变化对定程磨削尺寸的影响

张果，季军警

(成都天马铁路轴承有限公司 技术一部，成都 610306)

符号说明

D初——定位面的初始尺寸(指调整过程中工件滚道直径)

D变——磨削过程中滚道直径

D1正——调整过程中大挡边外径

D1变——定位面尺寸为D变时，未磨削外径尺寸(与D1正相等)

D1实——磨削过程中大挡边外径直径

d正——调整过程中的内径

d变——定位面尺寸为D变时，未磨削内孔尺寸(与d正相等)

d实——磨削过程中的内径

f——定位面尺寸变化对磨削面尺寸的影响量(外径影响量f1,内孔影响量f2)

R砂——砂轮半径

OJ——初始定位面尺寸工件中心与砂轮中心的距离

OO′——定位面尺寸由D初变为D变时，工件中心在电磁无心夹具上移动的距离

MP——定位面尺寸为D变时，实际定程磨削工件磨削面半径尺寸距初始对刀工件磨削面半径尺寸的距离

P点——定位面尺寸为D变时，砂轮和工件表面磨削的切点

α——支承角

β——支承夹角

1 概述

铁路轴承353130B内圈结构如图1所示，其大挡边外径是装配油封的油封面，要求与滚道、内径具有良好的同心度。为消除由于工序定位基准不一致对同心度的误差影响，工艺顺序安排以滚道面做基准支滚道磨滚道，然后以滚道定位对大挡边外径和内孔进行加工。磨削方法属于以外圆定位磨另一外圆、以外圆定位磨内径面范畴。

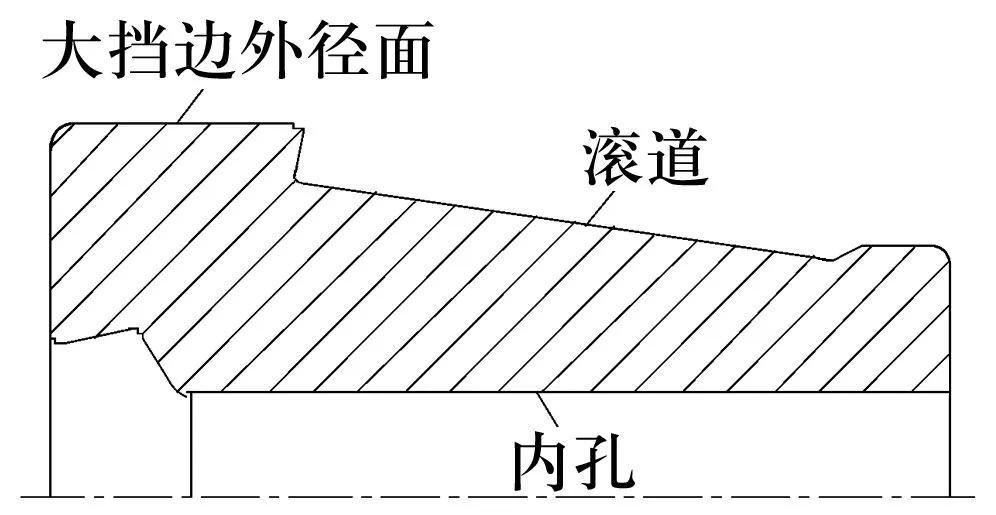
图1 353130B轴承内圈结构示意图

套圈磨加工过程中被磨削表面的尺寸精度控制方法主要有：定程法和主动测量法[1]。采用3ME2116半自动机床对工件大挡边外径面进行磨削，用MZ2015C半自动机床对工件内径面进行磨削，尺寸控制方式为定程法。经分析，在机床、砂轮及夹具相关调整参数固定不变时，用定程法磨削外径和内孔，定位面尺寸有一定公差时，会造成大挡边外径和内孔尺寸偏差。

2 电磁无心夹具定程磨工件尺寸变化

电磁无心夹具起径向定位作用的部件为前、后支承[2]。在定程磨削过程中，设定位面初始尺寸和磨削面的初始尺寸均为技术要求规定的名义尺寸，当定位面由初始尺寸增大或减小到另一尺寸时，磨削面尺寸也将由初始尺寸减小或增大到另一尺寸，磨削面尺寸减小与增大的变化量与支承角、支承夹角、砂轮半径、定位面尺寸变化量有关。

2.1 滚道定位磨外圆

图2为以外圆定位磨另一外圆的磨削原理，由图可知，当定位面直径由D初变为D变时，工件中心由O点移至O′点，处于第1象限；工件与前、后支承的切点发生变化，两支承间的定位弦长由BF移至AG，AB和FG分别为工件与前、后支承切点的移动距离；OO′连线的延长线与前、后支承切线相交于N点。由几何关系可知，砂轮圆周与工件外圆属于外切，其切点与砂轮中心、工件中心处于同一直线上。由于外圆磨削所用的砂轮直径较大，接触弧较短，砂轮半径对磨削面的尺寸影响较小。

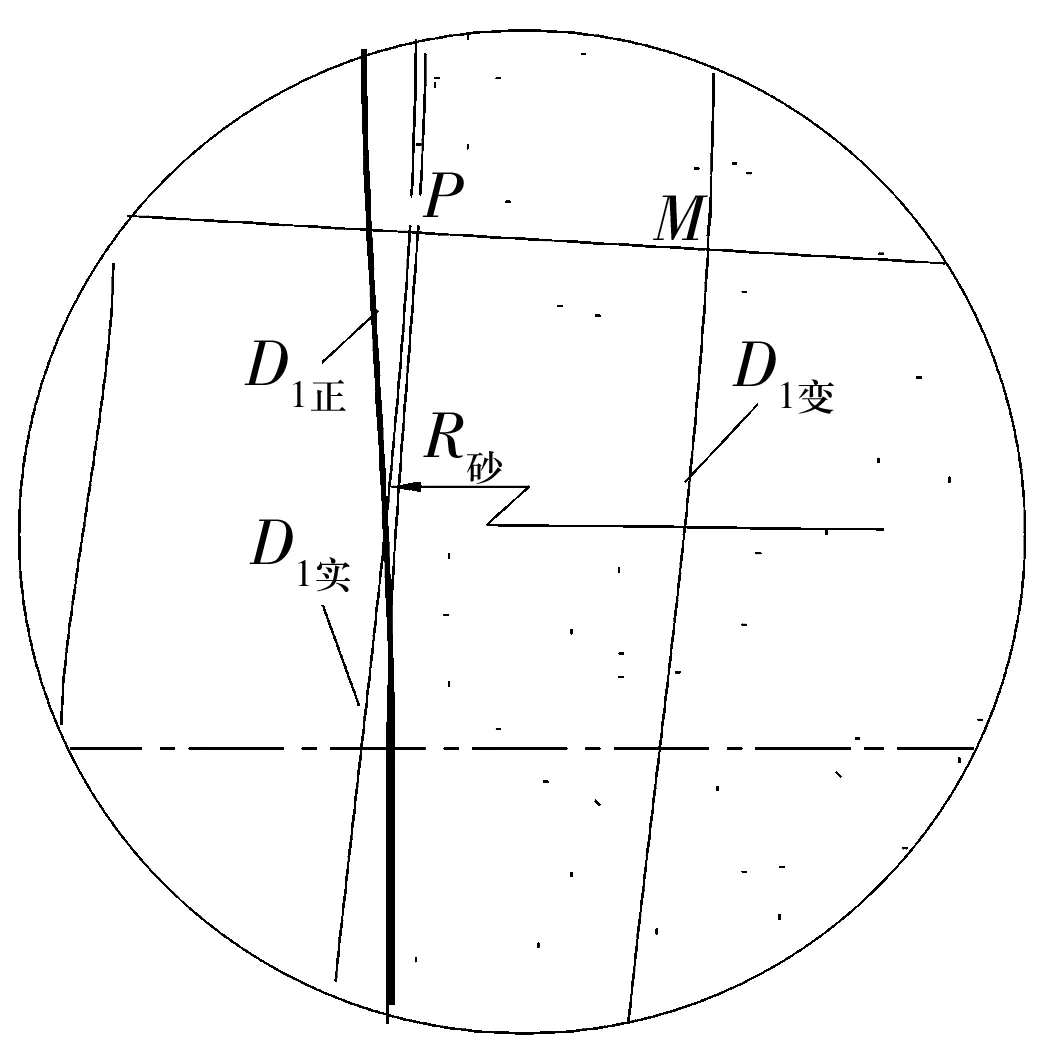
图2 电磁无心夹具以外圆定位定程磨另一外圆的几何关系

当定位面直径由D初变为D变时，对磨削外径面尺寸影响量为

f1=2MP=2(O′M-O′P)。

(1)

由图2几何关系可得：

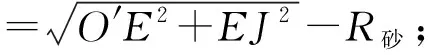
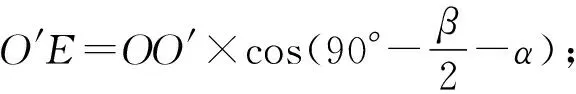
从而得出，磨削外径面的尺寸偏差量为

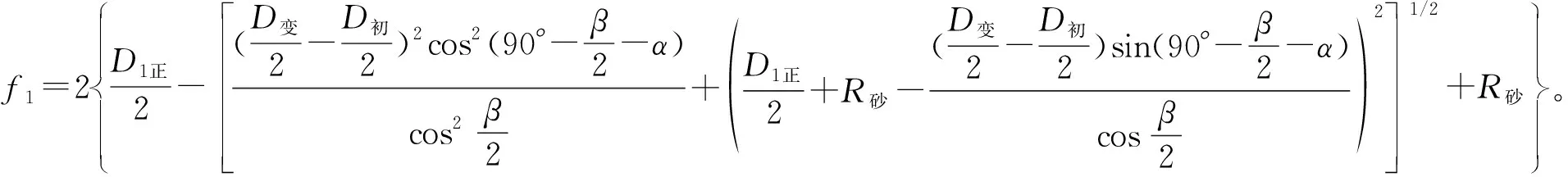
(2)

2.2 滚道定位磨内孔

图3所示为以外圆定位磨内孔的磨削原理，当定位面直径由D初变为D变时，工件中心由O点移至O′点，处于第2象限，工件中心与支承、支承夹角的几何关系与磨外径面一致。由几何关系可知，砂轮圆周与工件内径属于内切，其切点与砂轮中心、工件中心处于同一直线上。由于内孔磨削所用的砂轮直径较大，接触弧较短，砂轮半径对磨削面的尺寸影响较大。

对磨削内孔面尺寸影响量为

f2=2MP=2(O′P-O′M)。

(3)

由图3几何关系可知

图3 电磁无心夹具以外圆定位定程磨内孔的几何关系

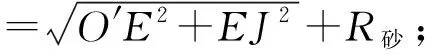
从而得到

(4)

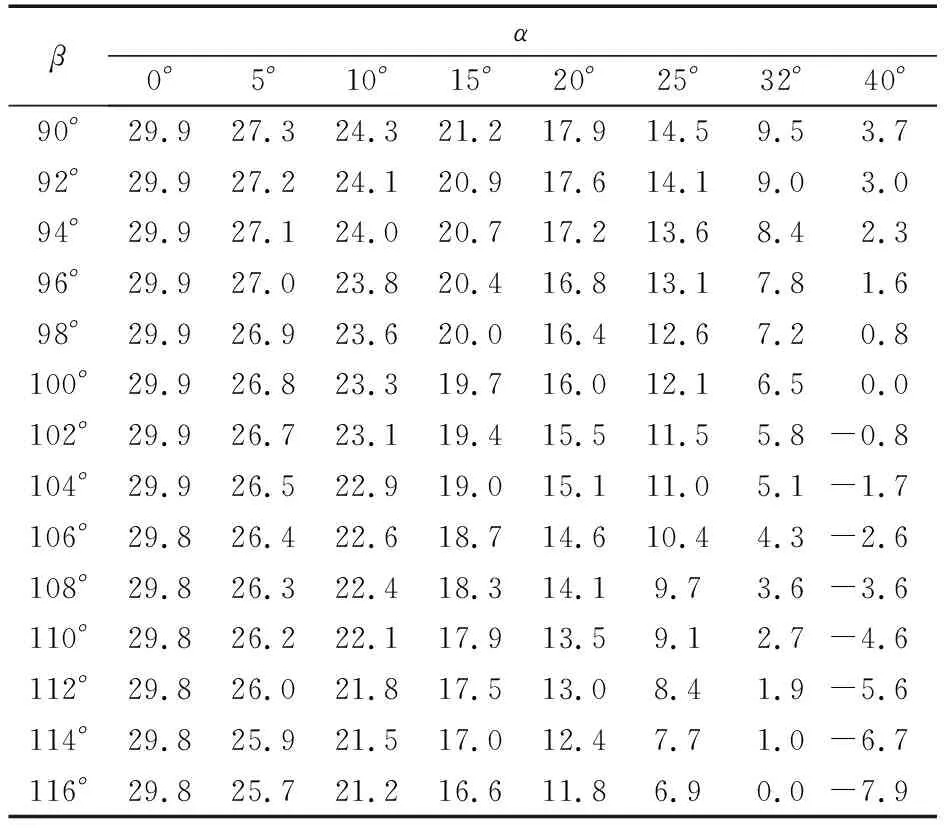
由(2)和(4)式可知，在电磁无心夹具上，用定程法磨削，在初始工件位置调整合格后，以外圆为定位面，磨外径时尺寸与参数D变，D初，D1正，R砂，α及β有关；磨内孔时与参数D变，D初，R砂，d正，α及β有关。当D变>D初时，f1(f2)的计算结果为正值，表示定位面尺寸欠磨时外径(内孔)磨削面尺寸的过磨量；当D变

3 电磁无心夹具参数对f的影响

3.1 支承夹角

设D初=188.775 mm，D变=188.805 mm，D1正=199.255 mm(公差中间值)，d正=149.979 mm(公差中间值)。因砂轮为选型确定，砂轮的尺寸变化在此处不予考虑。由(2)和(4)式可得在砂轮直径不变、支承夹角不同时，滚道尺寸变化量(已知定位面偏差为0.03 mm)对大挡边外径及内孔尺寸变化量的影响值，计算结果见表1、表2。 由表中数据的变化趋势可知：

表1 定程磨大挡边外径面时电磁无心夹具支承角对f1值的影响 μm

表2 定程磨内孔时电磁无心夹具支承角对f2值的影响 μm

(1) 当α=0°，β=90°时，定位面欠磨0.03 mm，与大挡边外径过磨量0.029 9 mm和内孔面过磨量0.030 01 mm均不等。这是因为定位面欠磨，尺寸变化后的工件相对于初始对砂轮工件的中心移动了一段距离，造成大挡边外径与砂轮的外切点由初始位置移至第1象限(若定位面过磨时，则外切点移至第4象限)，采用定程磨降低了其影响值；内孔磨削面与砂轮的内切点移至第4象限(若定位面过磨，则内切点移至第1象限)，增大了其影响值。

(2) 当α=0°时。定程磨外径面，尺寸变化后的工件对外径尺寸的影响量随着β角的增大而降低；定程磨内孔，对内孔尺寸的影响量随着β角增大而增大。这是因为在α=0°时，不论定程磨外径或内孔，β角的增大均能使尺寸变化后工件的磨削面超过砂轮初始位置的距离减小。但内孔磨削前支承处于水平状态，砂轮与工件的接触弧很长，反而增大了其影响量。

(3) 定程磨外径或内孔时，α角越大，β角的增大能降低因定位面尺寸变化造成的大挡边外径或内孔尺寸的变化量，且下降速度比α角较小时的下降速度要快。

(4) 当前、后支承调整至α+β/2>90°时，定位面的欠磨(0.03 mm)不会使大挡边外径或内孔尺寸过磨，反而会使大挡边外径或内孔欠磨。这是因为支承角、支承夹角增大后，定位面变化的工件中心已经处于第2象限(磨外径)或第1象限(磨内径)。此条件属理论计算，在实际生产中为保证电磁无心夹具夹持力、偏心量等，其前、后支承不会调整到此角度值。

结合353130B的工艺调整参数，由上述计算过程可得，当内圈滚道欠磨0.03 mm时，定程磨大挡边外径则最大过磨量为0.021 2 mm，最小过磨量为0；定程磨内孔时最大过磨量为0.030 03 mm，最小过磨量为0.000 14 mm。当内圈滚道过磨时，其计算结果均带负号，绝对值与表1、表2中数据一致，表示大挡边外径或内孔尺寸的欠磨量。

进一步计算发现，当α为负值时，β的增加将会增大定程磨大挡边外径或内孔尺寸的影响量，α的绝对值越大，则β的增加将会越快地增大定程磨大挡边外径或内孔尺寸的影响量。这与α为正值的情况相反，因为α为负值时，定位时会将工件大挡边外径或内孔向砂轮中心方向推动的距离增大，因此，在生产调整中要避免α角为负值的情况。

3.2 其他参数的影响

对f1(f2)的影响不仅与α和β有关，而且还与D变，D初，D1正(d正)，R砂有关。在α和β角保持不变的情况下，D变，D初，D1正(d正)，R砂对f1(f2)的影响如下：

(1)D变与D初的值相差越大，工件定位面尺寸稳定性越差，其对定程磨削外径面或内孔面的影响量越大。

(2)D1正和d正对f1和f2的影响由(2)式和(4)式可知：当D1正增大或减小时，f1随之增大或减小；当d正增大或减小时，f2随之减小或增大，但D1正和d正对f1和f2值的影响非常的小。因为D1正(d正)的变化仅表示工件与砂轮切点的变化，对f1(f2)的影响可忽略不计。

(3)磨大挡边外径面时，砂轮直径大，工件与砂轮的接触弧很短，砂轮半径对定程磨外径面的影响较小。磨内孔时，砂轮直径小，工件与砂轮的接触弧较长，砂轮半径对定程磨内孔的影响较大，砂轮半径的影响趋势为砂轮半径增大，影响量增大；砂轮半径减小，影响量随之减小。

3.3 优化措施

根据上述分析，为降低因定位面尺寸不稳定对磨削面精度带来的影响，在生产调整过程中，可采取以下措施来减小定程磨f1(f2)值：

(1) 在产品形状、位置公差合格的情况下，应增大α和β，并避免α+β/2>90°。

(2) 采取工艺方法，在磨削定位面时压缩其公差带，减小定位面的不稳定值，以保证定位面的精度要求。

(3) 当以外径面定位对内孔进行定程磨削时，在保证砂轮足够切削力、切削速度的情况下，应尽量减小砂轮直径。

(4) 在磨削加工中，能采用主动测量方法时应避免用定程法进行尺寸控制。

4 结论

(1) 定程法磨削外径面(内孔)时，定位面欠磨会导致外径面(内孔)过磨；定位面过磨会导致外径面(内孔)欠磨。

(2)α和β增大，能减小定位面欠磨或过磨时对外径面和内孔尺寸的影响，减小量受α和β增大量的控制。

(3) 当α+β/2>90°时，定位面的欠磨不会造成外径面和内孔面的过磨，反而使外径面和内孔面欠磨；定位面过磨也不会造成外径面和内孔面的欠磨，而会使外径面和内孔面过磨。因为工件中心所处的象限在α+β/2>90°时发生变化。

(4) 以外圆定位定程磨外圆时，砂轮半径对f1值的影响很小，可忽略不计。以外圆定位定程磨内孔时，砂轮半径对f2值的影响较大，必须予以考虑。

(5) 定程磨削中，初始对砂轮尺寸D1正(d正)是调整时必须得到的具体值，以便运用公式进行计算，为调整机床提供有益参考。

(6) 作为基准面的磨削定位面的尺寸公差应尽量小，以避免其散差较大而对磨削面造成过大的偏差。