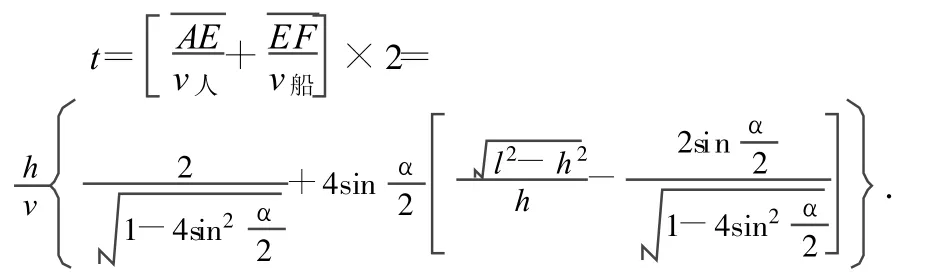妙用光学规律 巧解运动问题
叶玉琴
(安徽省安庆市第二中学,安徽安庆 246000)
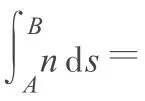
例1.如图1所示,P 、O、Q 为河岸上的 3点,其中 P、O连线垂直河岸,某人通过游泳(v1=3 m/s)和步行(v2=5 m/s)由P出发前往目的地Q.已知河宽L=100 m,O与Q间距150 m,问此人选择什么样的路径可以使他经历的时间最短?最短时间为多少?
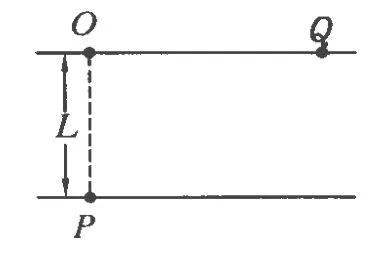
图1
解析1:这是一道看上去非常简单的运动学问题.问题的关键是此人在何处上岸,不妨假设此人在与O相距为x m的M点上岸,如图2所示,那么此人应该先沿PM方向游泳到M点再步行至目的地Q.
根据位移公式s=vt很容易得到
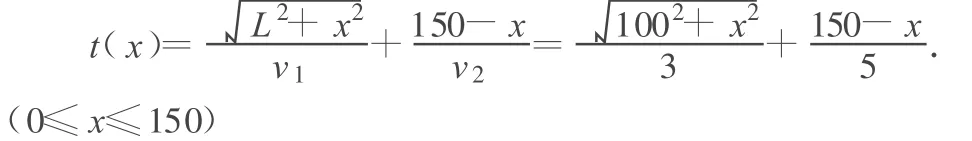
这题意及列式都比较简单,但 t(x)是关于 x的复合函数,利用中等数学知识难以求出 t(x)的最小值.下面利用高等数学求解.
先求t(x)关于x的一阶导数有
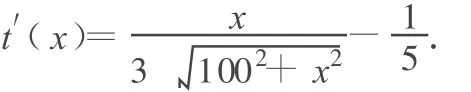
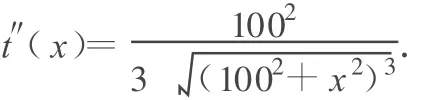
当 x=75时 t″(75)>0,根据费马原理可知
显而易见,以上的计算过程不仅十分繁难,而且中学生现有的数学知识难以求解,但类比光运动的特点可使这类问题的求解简单易行.
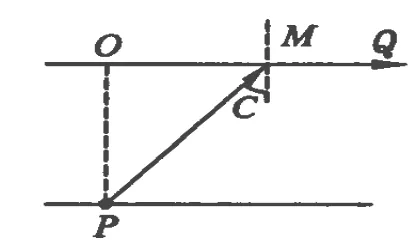
图3
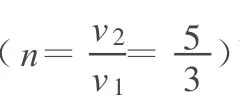
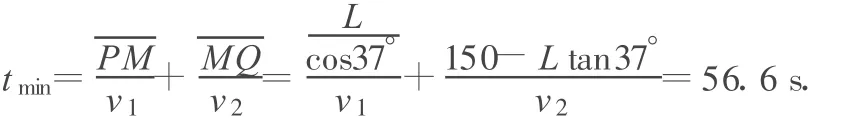
两种解法结果是一致的,但第2种方法由于类比了光的折射,巧妙地借助规律,因此非常简单.
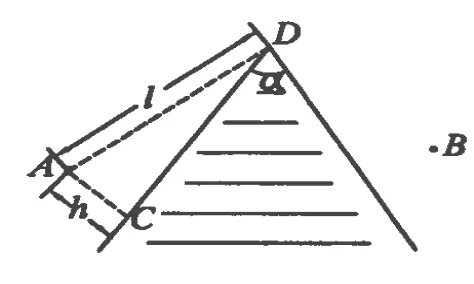
图4
例2.湖湾成顶角为 α的楔形,岸上住有一渔夫,他的房子在 A点,如图 4所示,从A点到他离最近的C点之距离为h,而到湖湾的一头,即到D点之距离为.湖对岸 B处有渔夫好友的房子,B点位置与A点相对于湖湾对称.渔夫拥有一只小船,他可以以速度v沿河岸步行或以速度乘船在湖中划行.求他从自己家中出发到好友家去所需要的最短时间t.
解析:本题可以利用高等数学求解.由于 A、B对称,所以路径关于角α的平分线对称,因此渔夫沿如图5所示的 A→E→G→B路径行走,设 E与D间距为x,则有
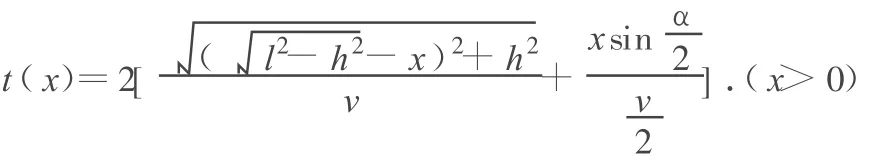
从上式不难看出,通过中等数学无法求解,即使利用高等数学来解也较繁难,但如果类比光学规律就可以很容易求解.本题中渔夫的运动十分类似光在棱镜中的折射情形,根据光学规律,光从 A点传播到B点的光路,同所有其他的路径相比,需时最少.又由于 A、B关于“棱镜”(即湖湾)对称和光路可逆性,所以在“棱镜”中的光线必垂直于角α的平分线,因此渔夫应该沿如图5所示的光路行走,即先沿 AE(令 γ为入射角)行走到湖湾E点,再乘船沿EG方向(EG垂直于角α的平分线)划行渡过湖湾,然后沿GB方向步行到B点.
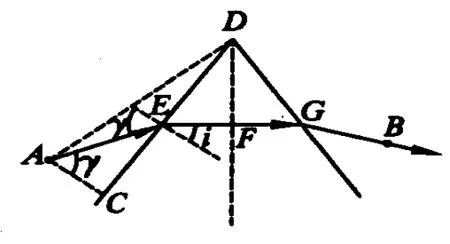
图5
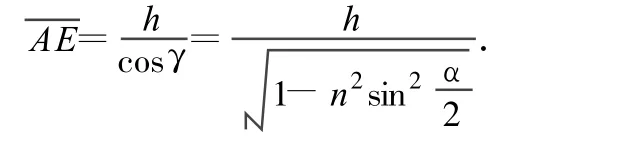
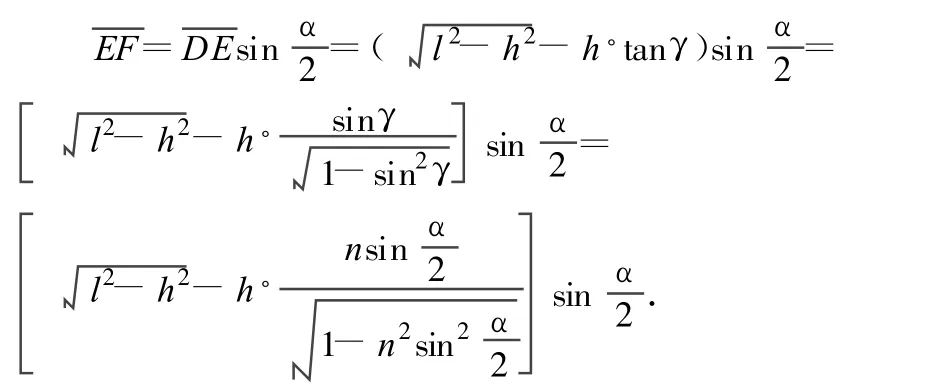
因此所求的时间为