“殊途不同归”,原因何在?
郑曙辉
(浙江省宁波第二中学,浙江宁波 315010)
2010年山东调研卷中有一道考题,该题考查运动学知识,同时考查运用数学知识处理物理问题的能力,情景新颖,运动模式既非匀速运动又非匀变速运动,是加速度随时间均匀减小的变加速运动,但求解的方法又在学生掌握的能力范围内.笔者把它作为一道习题布置给学生,结果引发学生的大争论,原因是采用两种不同方法做的学生都认为自己的解法完全正确,但结果却并不相同,而且这个差异也不在计算的误差范围内,可谓“殊途不同归”.原因何在?难道是其中一种方法有错误?笔者抓住这个契机,引导学生进行分析,查找原因所在,使学生通过争议,获取进步.
原题摘录如下:

图1
F1是英文Formula One的缩写,即一级方程式赛车,是仅次于奥运会和世界杯的世界第三大赛事.F1赛车的变速系统非常强劲,从时速0加速到100 km/h仅需2.3 s,此时加速度仍达10 m/s2,时速为200 km/h时的加速度仍有3 m/s2,从 0加速到 200 km/h再急停到 0只需 12 s.假定F1赛车加速时的加速度随时间的增大而均匀减小,急停时的加速度大小恒为9.2 m/s2.上海F1赛道全长5.451 km,比赛要求选手跑完56圈决出胜负.求:
(1)若某车手驾驶该赛车比赛时的平均速度为 210 km/h,则跑完全程用多长时间?
(2)该车手的F1赛车的最大加速度.
分析与解答:
该小题考查路程与平均速率的关系式,直接套用公式就可轻易求得答案,学生不会产生争议.争议的出现产生在第(2)小题中,下面对第2小题采用不同的方法进行解答.
方法1:联立方程组求解.
(2)F1赛车加速时的加速度随时间的增大而均匀减小,由题意可得:a=am-kt,其中am为赛车的最大加速度.
设赛车速度从200 km/h急停到零时,用时为t0,由运动学公式可得
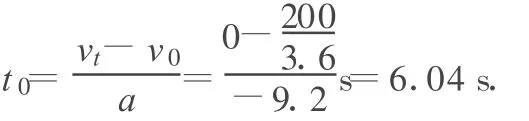
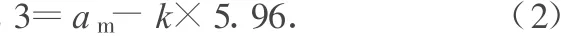
am=14.4 m/s2.
方法2:用a-t图像法求解
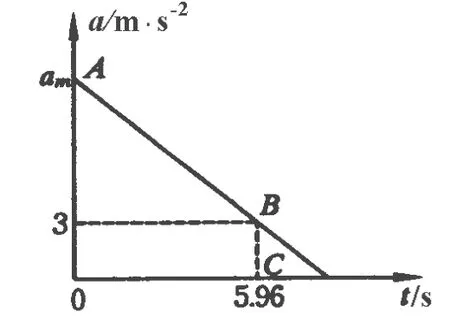
图2
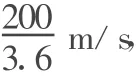
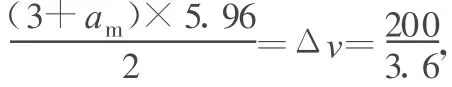
解得am=15.64 m/s2.
两种不同的方法,得到的结果相差了1.24 m/s2,这绝对不是计算误差所能简单解释的,引导学生对两种求解方法的每一步进行仔细推敲,发现方法都正确!问题究竟出在哪里?为了引发学生积极思考,笔者又提出了一种新的解法,开拓学生的思路.
方法3:等效平均加速度法求解.
(2)设赛车速度从200 km/h急停到零时,用时为 t0,由运动学公式可得
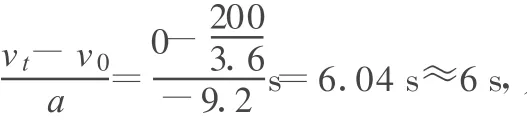
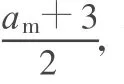
又一个不同的答案!
对方法3的答案和方法2的答案及其解答过程进行对照,容易发现,这两个答案其实在计算误差范围内,略有差异主要是在时间的计算上进行了近似处理,如果把方法2的时间与方法3的时间进行同样的处理,这两个答案是非常接近的,在计算误差范围内可以近似看做相等.这样,答案就倾向于am=15.4 m/s2了.
上述3种求解方法的思路各异,途径各不相同,但方法正确.方法1和后两种方法的答案为何会出现较大的偏差?再仔细分析这3种解法,发现后两种都没有用到时间在2.3 s时加速度达10 m/s2这一组数据,而方法1是采用时间在2.3 s时,加速度达10 m/s2和时间在5.96 s(或近似为6 s)时,加速度为3 m/s2时建立两个方程解得.可见造成答案偏差的问题就出在当时间为2.3 s时,加速度达10 m/s2这一组数据不精确,2.3 s,10 m/s2不在 a-t图线上.因此,笔者建议把该题的“从时速0加速到100 km/h速度仍达 10 m/s”,改为“从时速0加速到100 km/h仅需2.6 s,此时加速度仍达 10 m/s2”.依此条件建立的两个方程组为
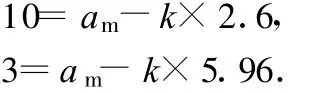
解得am=15.42 m/s2.这样,3种方法求得的结果便一致了.
一个数据的瑕疵影响了整道题目的质量.这道题目的求解告诫我们,出题者除了把握科学性、知识性以外,对题目中所涉及到的每一个数据也要进行推敲,以免出现不应有的错误.教师在讲解具体题目过程中,如果碰到了这种情况,更要抓住教学契机,引导学生进行正确、有效的讨论,这样“殊途”才能“同归”,而不能随意以题目有误应付了事.这样做的目的,除了对知识的尊重以外,更重要的是在对学生激发学习兴趣的同时,也培养了学生严谨的科学态度,这比掌握一道习题的求解更为重要!

