模糊自适应PID控制器在集中供热系统中的应用

许青松，高经伍，刘 冰，杜 娟

(东北电力大学 自动化工程学院，吉林 吉林 132012)

随着供热事业的迅猛发展，对供热系统提出了更高的要求。因此有必要对集中供热进行深入研究，以提高集中供热系统的自动化程度，不断增强供热系统运行的鲁棒性、准确性、节能性和自适应能力。

集中供热系统是个非常复杂的动力学系统，具有大时滞、大惯性、非线性、时变及不确定等特点[1]。采用模糊控制技术与PID控制技术相结合而构成模糊自适应PID控制器的方法[2]，在集中供热系统中得到了广泛的应用。

1 集中供热系统的数学模型辨识

1.1 数学模型的辨识

根据集中供热系统的特点，其数学模型可表示为：

式中，n为系统的阶数，T为时间常数，Kp为比例放大系数，τ为滞后时间常数，s为采样时间。

由于本文中热工对象的复杂性，用解析的方法很难得出动态特性的精确数学表达式，因此采用在运行的条件下通过实验来获得对象的动态特性的方法，根据对象动态响应曲线的特质求取相关特性参数。实验中的输入信号为阶跃信号，在阶跃输入下得到对象的阶跃响应曲线。

该实验是在调试吉林市某换热站设备时进行的一次试验，操作步骤如下：改变一次网供水阀门开度，阀门开度在某一时刻由35%开至60%，一次网供水流量由60 t/h跃升为80 t/h，然后每隔10 s采样一个二次网供水和回水温度数据，共采样100次，即1 000 s的温度数据，再取它们的平均值。实验数据如图1所示。

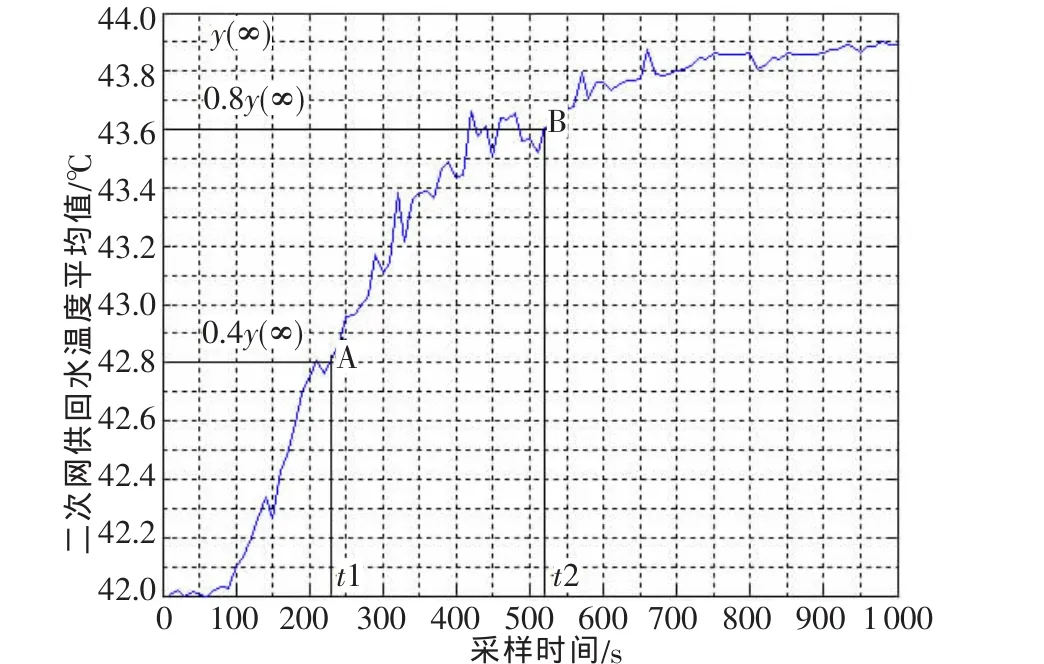
图1 系统阶跃响应曲线

根据先验知识，系统的阶跃响应曲线具有自平衡能力，可采用两点法求取特性参数。

两点法不需要画出整个阶跃响应曲线，只根据最终稳 态 值 y(∞)， 分 别 估 计 出 0.4y(∞)和 0.8y(∞)所 对 应 的 时间t1和t2，由近似公式计算特性参数。两点法适用于对象传递函数阶数n＜6的场合。

方法如下：

(1)测定或估计阶跃响应曲线的最终稳态值y(∞)；

(2)在阶跃响应曲线上求取 y(t1)=0.4y(∞)所对应的时间t1；

(3)在阶跃响应曲线上求取 y(t1)=0.8y(∞)所对应的时间t2；

(4)由近似公式计算特性参数：

滞后时间常数τ：根据阶跃响应曲线脱离起始的毫无反应的阶段，开始出现变化的时刻，就可以确定参数τ。

观察图 1可以得出，t1=230 s，t2=520 s， 并将 t1和 t2带入式(3)得n=1.83，取与之最接近的整数得 n=2；再将t1、t1和 n带入式(4)得 T=173.61。 该系统输入为 q=23，则比例系数KP=1.91，滞后时间常数 τ=60 s可直接观察得出。如此，该系统的数学模型可用带纯滞后环节的二阶系统来表示：

1.2 验证模型的合理性

表1给出了高阶惯性对象1/(Ts+1)n中阶数与比值t1/t2的关系，由计算可得 t1/t2≈0.442 3，查表可知与 0.46最接近。因此，该系统可以用二阶系统来近似。

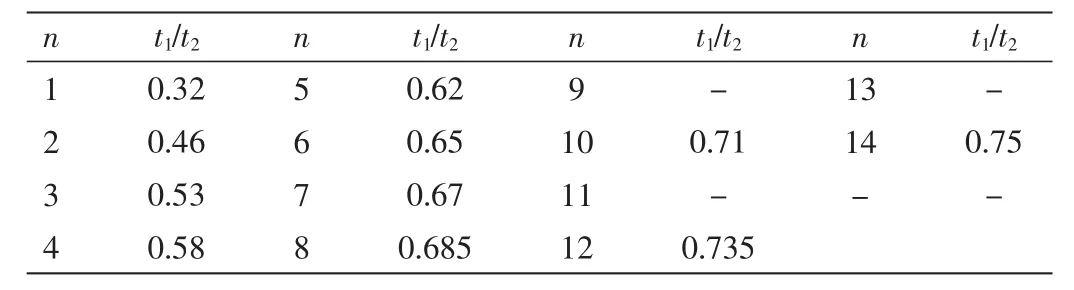
表1 高阶惯性对象1/(Ts+1)n中阶数与比值t1/t2的关系

2 模糊自适应PID控制器设计

2.1 PID控制原理

PID控制算式表示为：

式(6)中，Kp、Ki、Kd分别表示比例增益、积分增益和微分增益。Kp的作用在于加快系统的响应速度，提高系统的调节精度。Kp越大，响应速度越快，调节精度越高。但Kp过大将产生超调，甚至导致系统不稳定。Ki的作用在于消除系统稳态误差，Ki越大，静差消除越快。但过大就会产生积分饱和而引起大的超调，影响系统的动态性能。Kd越大，系统抑制超调能力越强，但过大会使被控量调节时间变长并使系统抗干扰能力下降[3]。

2.2 模糊自适应PID控制器设计

模糊自适应PID控制器主要由参数可调整的PID控制器和模糊推理器两部分组成。模糊推理器以偏差e和偏差变化率ec作为输入，以常规PID控制器的三个参数Kp、Ki、Kd为输出，采用模糊推理方法实现对参数 Kp、Ki、Kd的调整，以满足不同时刻偏差e和偏差变化率ec对PID参数自调整的要求，其基本结构如图2所示。

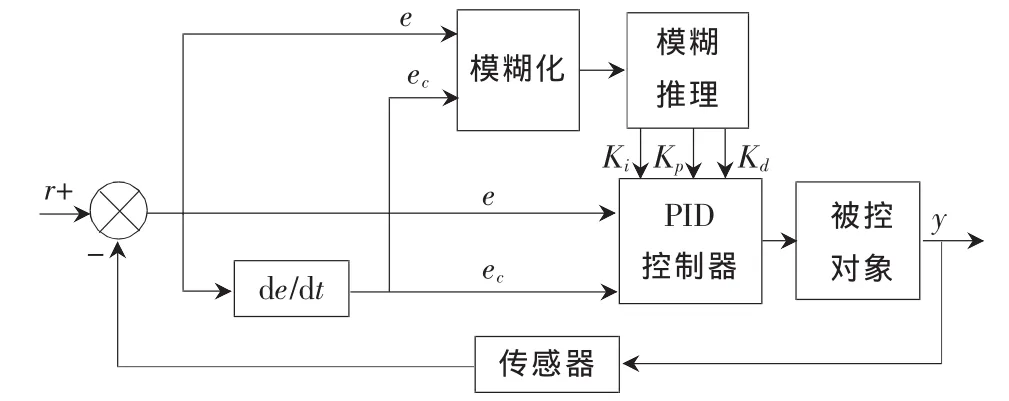
图2 模糊自适应PID控制器的结构

模糊自适应PID控制是通过计算当前系统偏差e和偏差变化率 ec，考虑 Kp、Ki、Kd三者的关联，根据工程设计人员的技术知识和实际操作经验，选择输入语言变量为偏差e和偏差变化率ec，语言变量值选取七个模糊子集{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)；选择输出语言变量为 △Kp、△Ki、△Kd，输出语言变量值也取{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)}。 模糊论域均为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，隶属度函数均为三角形型、S型、Z型隶属度函数。

表2为根据上述规则制定的输出变量 △Kp(△Ki、△Kd同理)的模糊控制规则表。

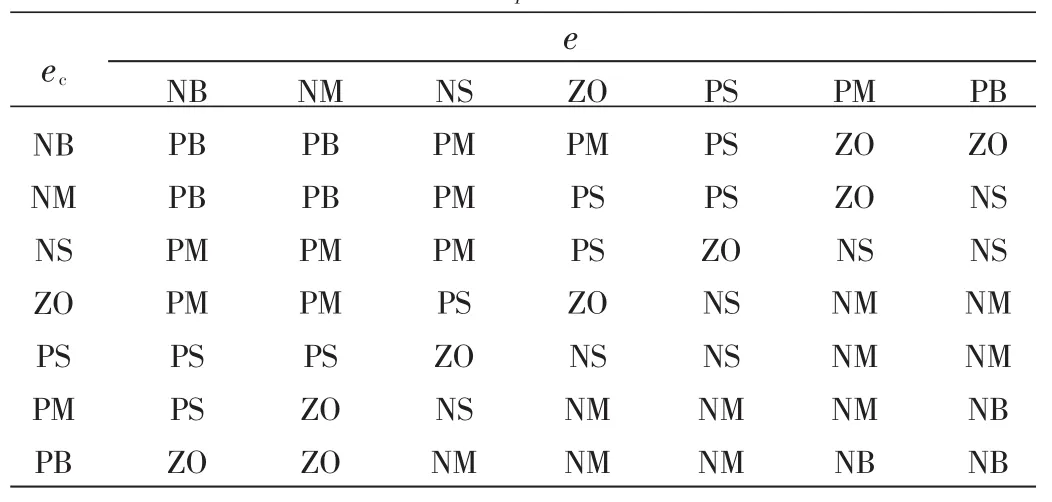
表2 输出变量△Kp的模糊控制规则表

根据模糊控制规则表，选择适当的模糊化和去模糊化方法，可以对 Kp、Ki、Kd进行在线动态调整，设 K′p、K′i、K′d为采用常规PID控制器的预整定值，计算公式如下：

在线运行过程中，控制系统通过对模糊控制规则的结果处理、查表和运算，完成对PID参数的在线自调整。

3 模糊自适应PID控制器MATLAB实现

本模糊控制器仿真程序是以m文件的形式给出的，需要运行时，只要把此m文件程序放到Matlab软件中直接运行即可，不需要其他任何操作[4]。

运行仿真程序，Matlab中仿真模糊推理和模糊判决生成的比例微分积分调节量观察曲面如图3所示。

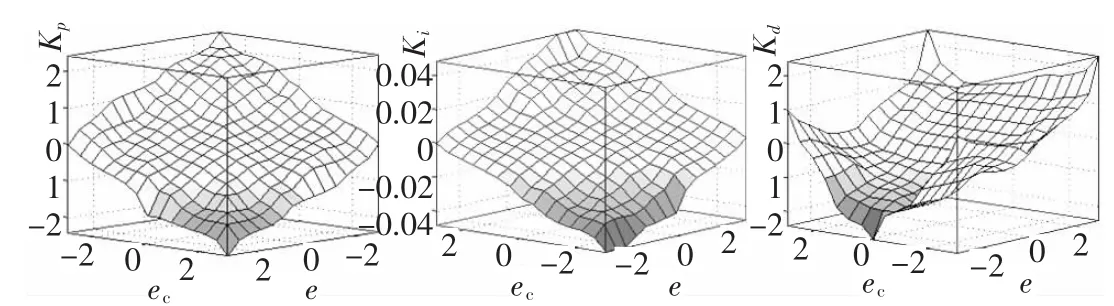
图3 比例积分微分调节曲面

在0.3 s时刻加入一个扰动信号，常规PID控制器和模糊自适应PID控制器输出的阶跃响应曲线分别如图 4、图 5所示。

图4 常规PID控制器的输出曲线

由图4、图5比较可以得出，模糊自适应 PID控制器较常规PID控制器对扰动具有更好的适应性、鲁棒性和稳态特性。应用于集中供热这种模型比较复杂、控制精度要求不高的系统，达到了预期的调节效果。

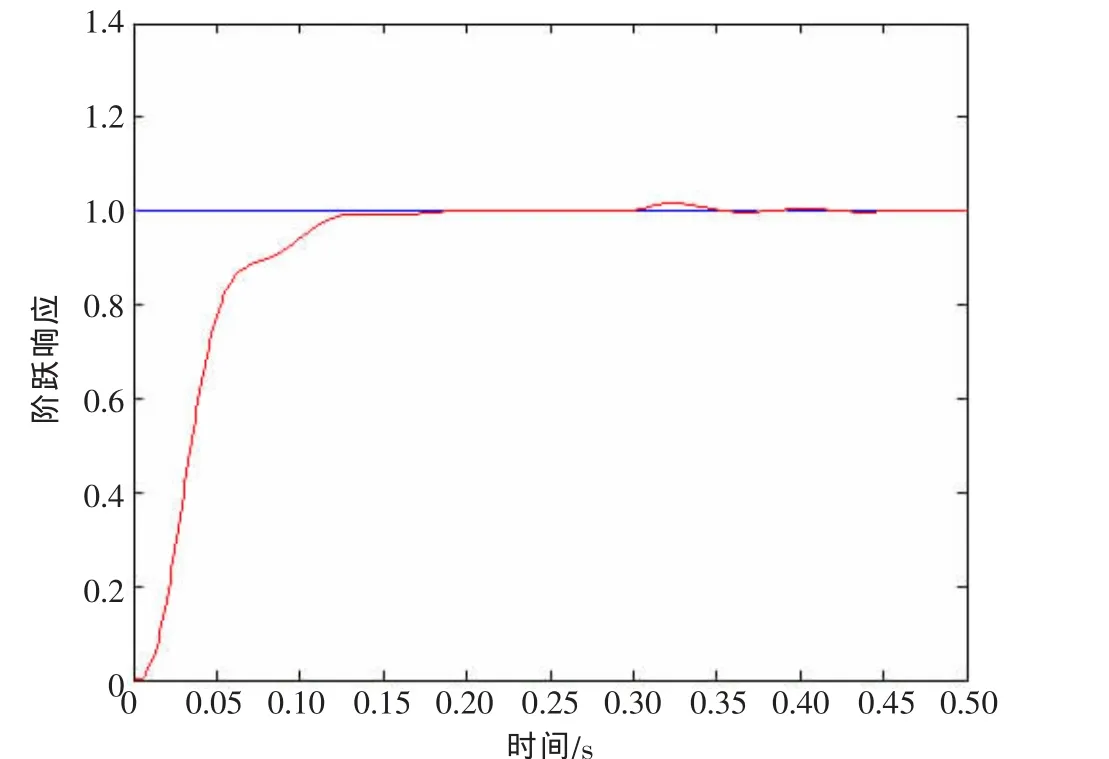
图5 模糊自适应PID控制器的输出曲线

模糊自适应PID控制器可用模糊推理的方法在线动态调整PID参数，能够发挥PID和模糊控制两者的优点，对被控系统的适应性强、鲁棒性好。特别在集中供热这样参数易发生时变的复杂系统中，可以获得令人满意的控制效果，能很好地适应了实际生产过程中的控制要求，而且达到节能减排的目的。由此可见，模糊自适应PID调节方式在集中供热系统应用中的合理性。

[1]张永明，朱学莉.供热负荷时间序列混沌特性识别及区间预报[J].暖通空调，2009，39(11)：50-53.

[2]袁凤莲.Fuzzy自整定PID控制器设计及其MATLAB仿真[J].沈阳航空工业学院学报，2006，23(1)：71-73.

[3]刘金琨.先进 PID控制及其 MATLAB仿真[M].北京：电子工业出版社，2003.

[4]黄忠霖，黄京.控制系统 Matlab计算及其仿真[M].北京：国防工业出版社，2009.