扁平绕带压力容器内爆炸动力响应数值模拟

孙 宾，田锦邦

(太原科技大学应用科学学院，山西太原 030024)

0 引言

多层压力容器在材料的合理利用、安全性等方面具有特殊的优点［1］。爆炸容器作为特殊的一类密封压力容器［2］，可对爆炸能量或爆炸装置产生的危险物进行有效限域，对有害气体进行密封，对外界起到防护作用，因此，在很多领域发挥越来越重要的作用［3－5］。

扁平绕带式压力容器的主要结构是内筒和筒外以一定角度交错缠绕的钢带，这种离散化的结构形式，使扁平绕带式爆炸容器在材料加工、生产成本、生产效率等方面具有整体式爆炸容器无法比拟的优势。

文中针对不同缠绕倾角和不同装药形状应用ANSYS/LS－DYNA非线性有限元程序进行数值模拟并与试验相比较，分析两种因素对容器抗爆特性的影响。

1 数值模拟模型

1.1 有限元模型的构建

建模时采用统一的单位制为:cm－g－μs。扁平绕带爆炸容器，应用ANSYS前处理程序建模，模型的几何尺寸与实验容器［6］保持一致。图1示出了扁平绕带爆炸容器的结构模型。

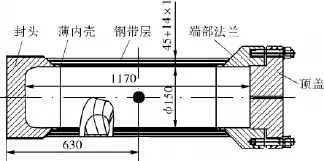
图1 绕带容器结构示意

表1列出分网后的单元数目和节点数，图2，3示出了扁平绕带容器和空气的划分网格后的模型。图4，5示出了柱形和球形炸药模型。

1.2 材料模型及参数

容器内壳﹑外壳和封头的材料参数见表2。

图3 空气有限元模型

图4 柱形炸药模型

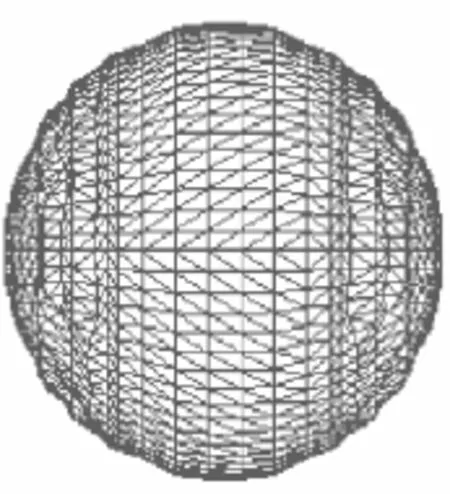
图5 球形炸药模型

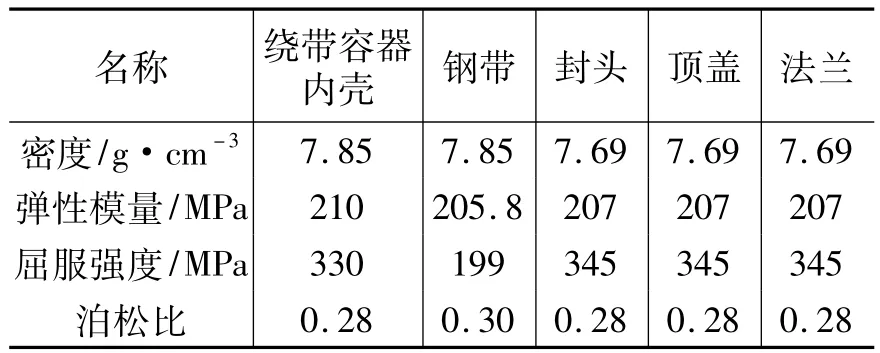
表2 容器材料参数［6］

炸药单元选用*MAT_HIGH_EXPLOSIVE_BURN模型［7］，爆速、爆压参数选取较符合此次试验的数据，分别为 0.4589 cm/μs和 5.37 GPa，用JWL状态方程描述爆轰过程压力和内能及相对体积的关系，该方程形式如下:

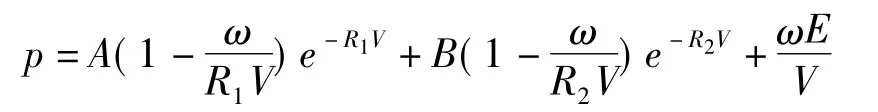
式中 A，B，R1，R2，ω——材料常数，分别为 373 GPa，3.33 GPa，4.15，0.95，0.28

V——相对体积

E——初始内能密度

空气密度 ρ0=1.293 ×10－3。

1.3 应变率效应模型及参数

在材料的塑性变形阶段，应变率效应通过Cowper－Symonds模型来考虑，其考虑应变率时的屈服应力为:

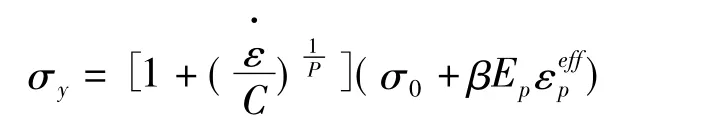
式中 C，P，β——Cowper－Symonds应变率参数，取 C=4 ×107，P=5.0，β =1

Ep——塑性强化模量，Ep=EtE/(E －Et)

E——弹性模量

Et——切向模量

σ0——初始屈服应力［7］

1.4 流固耦合的实现

文中划分的单元采取ALE算法，因为ALE算法更适合处理整个物体有空间大位移并且自身有大变形等问题。

对模型进行映射分网，空气和容器内壳在交接处设置共节点，以此来实现两者的耦合［7］。通过程序中的初始体积分数设置炸药位置、形状和体积，程序计算开始后会在初始化阶段将炸药填充到所定义的位置、形状和体积。这样既简化了建模过程又不影响网格的划分质量［8］。

容器内壳和绕带层之间均采取自动单面接触选项来定义接触。

2 计算结果与分析

2.1 缠绕倾角

图6示出了绕带倾角为10°，15°、在装475 g柱形炸药(试验采取的是柱形装药［6］)情况下，爆炸加载试验后容器的变形和数值模拟变形情况对比，可发现试验和数值模拟的情况基本吻合;表明数值模型建立的合理性。

表3 列出了绕带倾角为 10°，15°，20°、在装475 g柱形炸药情况下，爆心位置最外层绕带的径向变形对比，试验值［6］与模拟值之间存在一定误差，但对于爆炸冲击这么复杂的过程，这种误差是可以接受的，因此所建立的数值模拟有限元模型是可靠的。

图7 示出了绕带倾角为 10°，15°，20°、在装475 g柱形炸药情况下，容器的爆心位置最外层绕带的有效塑性应变，发现缠绕倾角越大，有效塑性应变越小。

图6 容器鼓胀图

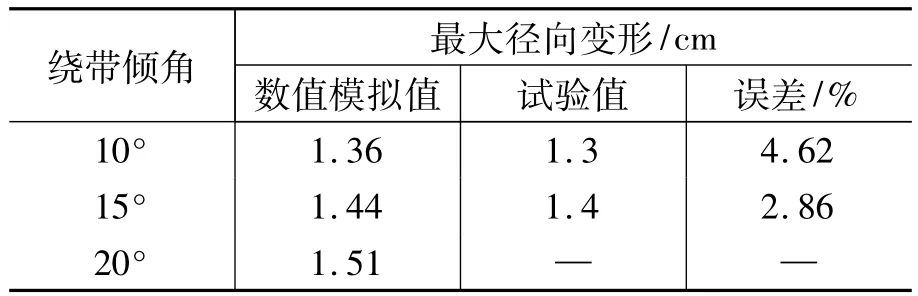
表3 爆心处容器变形对比

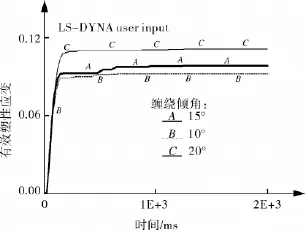
图7 有效塑性应变图

从爆心处的径向变形和有效塑性应变数值可看出，绕带的倾角越小，容器的抗爆特性越好。

2.2 装药形状

在爆炸容器动力响应过程中，爆炸产生的冲击载荷是非常重要的一个因素，同等重量下球形和柱形装药对扁平绕带式爆炸容器产生的冲击载荷是不相同的。图8示出了装有400 g球形和柱形炸药情况下，倾角为10°的容器壳体外壁上11个均匀的应力峰值检测点的最大等效应力分布曲线，图9示出了该情况下封头从边缘到顶心位置的最大等效应力分布曲线。球形装药下爆心环面和封头顶心的最大应力分别为等重柱形装药时的78.23%和50.01%;在壳体外壁上距爆心5 cm处，柱形装药和球形装药下的最大等效应力分别为各自爆心处的54.73%和71.25%，在远离爆心位置的一部分应力点的应力，球形装药会大于柱形装药的情况，再结合封头上的应力分布曲线，可以推断出球形装药的爆炸作用要比柱形装药的均匀。

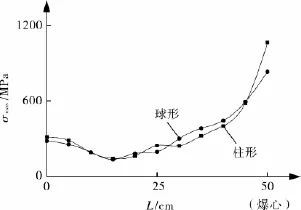
图8 壳体等效应力分布曲线

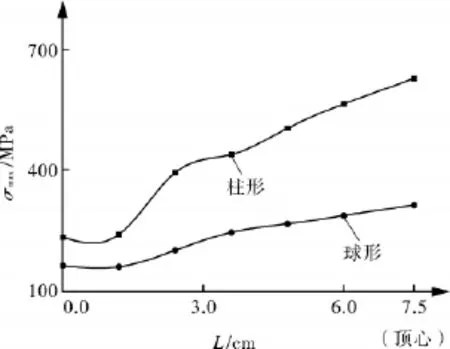
图9 封头等效应力分布曲线

图10，11 分别示出了 10°，15°，20°三种倾角的扁平绕带爆炸容器在400 g柱形装药和球形装药情况下的爆心处的内壳反射超压曲线。结果表明:装同种形状炸药的三种容器爆心处的反射超压相差不大，而三种容器在柱形装药情况下的反射超压分别为球形装药时的1.72，1.73和1.72倍，与文献［9］的试验数据比较吻合。表明，装药形状对反射超压产生影响。这主要是由于空气冲击波在传播中不断均匀化造成的。

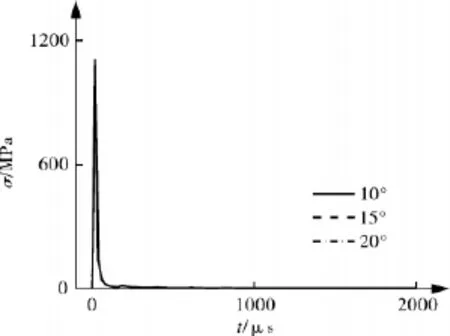
图10 柱形炸药下压力曲线

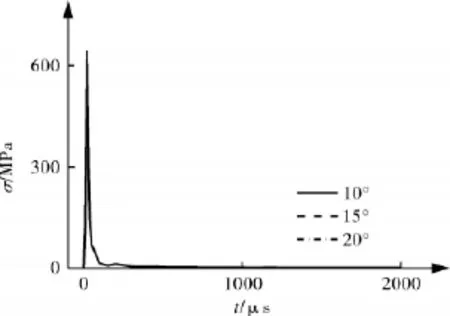
图11 球形炸药下压力曲线

3 结论

通过数值模拟与试验验证，得到以下结论:

(1)模拟值与试验值的误差在5%以内，这对相对复杂的爆炸冲击过程而言是可以接受的，表明建立的数值模拟模型是可靠的，为以后扁平绕带压力容器在内部爆炸载荷作用下的研究提供了相对可靠的有限元模型。

(2)随着缠绕倾角的增加，钢带对容器的轴向抗爆能力增加，而环向抗爆能力恰恰相反，爆炸冲击载荷下的内壳环向应力大于轴向应力，因而缠绕倾角越大，抗爆特性越小。这在数值模拟和试验数据中得到了验证。

(3)在同等重量下，装药的形状对冲击载荷产生影响，且球形装药在爆心处产生的反射超压比柱形产生的小，且爆炸作用更加均匀。

［1］李南京，朱孝钦，宋鹏云，等.多层压力容器的研究及其进展［J］.化工机械，2008，35(6):368 －373.

［2］朱文辉，薛红陆.爆炸容器动力学研究进展评述［J］.力学进展，1996，26(1):68 －77.

［3］霍宏发，于琴，黄协清.组合式爆炸容器冲击载荷及其动力响应的数值模拟［J］.西南交通大学学报，2003，38(5):513 －516.

［4］饶国宁，陈网桦，王立峰，等.内部爆炸载荷作用下容器动力响应的数值模拟［J］.中国安全科学学报，2007，17(2):129 －133.

［5］王定贤，王万鹏，石培杰，等.柱形爆炸容器动力学响应的有限元模拟与实验检验［J］.压力容器，2008，25(7):13 －16.

［6］田锦邦.扁平绕带式压力容器动力特性研究［M］.北京:中国建材工业出版社，2008.

［7］李裕春，时党勇，赵远.ANSYS11.0/LS－DYNA基础理论与工程实践［M］.北京:中国水利水电出版社，2008.

［8］尚晓江，苏建宇，王化锋.ANSYS/LS－DYNA动力分析方法与工程实例(第二版)［M］.北京:中国水利水电出版社，2008.

［9］林俊德.封闭空间的化爆荷载与沙墙消波［J］.解放军理工大学学报(自然科学版)，2007，8(6):559－566.