基于支持向量机回归的房地产单指标预测

王 平，师 青

（1.武汉工程大学 管理学院，武汉430071；2.中南财经政法大学 公共管理学院，武汉430073）

0 引言

支持向量机[1]是近年来发展起来的一种有效的非线性问题处理工具,它以统计学习理论为基础,以结构风险最小化为目标，因此能够克服BP神经网络和传统统计方法的诸多缺点,在训练样本有限的情况下,可很好地控制学习机器的推广能力。支持向量机作为一种新的机器学习方法，其理论体系完备，而且能够逼近任意复杂系统，因此在模式识别和数据挖掘领域得到了广泛的应用，但用于对复杂的时间序列进行预测则不多见，尤其是在房地产预警领域的运用目前还未曾见到，本文将支持向量机回归方法用来进行房地产单指标预测，并和BP神经网络预测法进行比较。

1 理论分析

1.1 支持向量机回归

设线性函数为f(x)=(wx)+b,则对ε不敏感函数逼近问题可转化为以下优化问题:

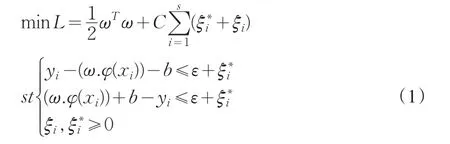
其中C=1/λ，为便于求解，将该二次规划（优化）问题转换为其对偶问题：

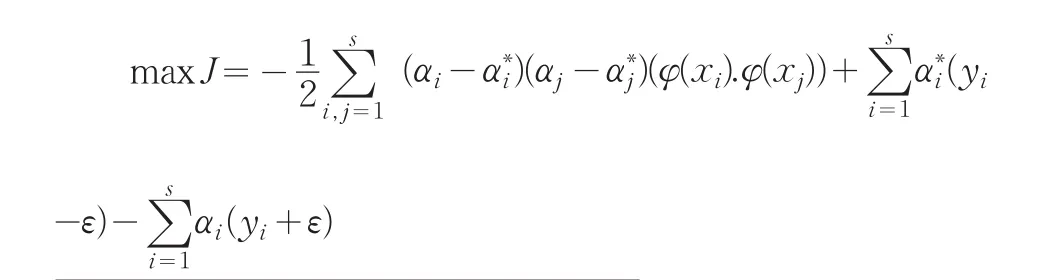
对于非线性逼近,基本思想是先通过非线性变换x→φ(x),将输入空间映射成高维的特征空间(Hilbert空间)[3],然后在特征空间中进行线性逼近,即f(x)=(w·φ(x))+b，这样目标函数式就变为：

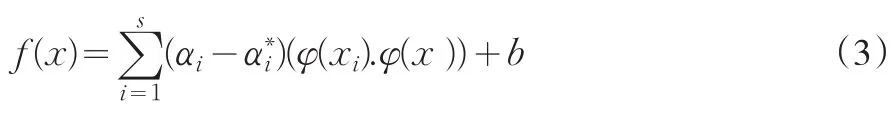
高维特征变换空间的内积运算即为支持向量机的核函数：

通过上面的分析可知，要求变量在高维空间的内积，只需在原低维空间计算其核函数即可，对凸二次规划问题进行求解，可得到如下非线性映射：

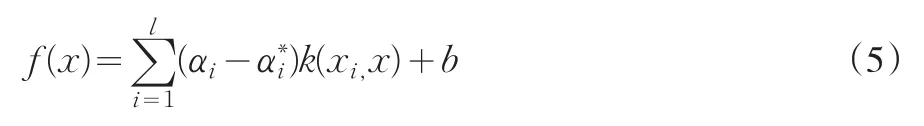
通常,上式中系数(α-α∗)只有一小部分不等于0,而这些系数不为0所对应的数据点就被称为支持向量。

1.2 时序相空间重构

由Kolmogro定理可知，对于任意一个时间序列，我们都可以把它看成一个系统，其输入、输出由非线性机制所决定。从这个意义上说，对时间序列进行预测，实质上就是根据历史数据求出映射f:Rm→Rn，然后用该映射来逼近数据中的非线性机制F，因此映射f就可以作为预测器使用[4]。

给定一个时长为N的时间序列{xt}，其中xt=x(t)，t=1,2,…，N，由于系统的演化规律可以在一个高维的相空间中恢复，因此，我们可以在短期内对时间序列{xt}进行预测。如果在某种条件下对满足特定条件的m，可以找到一个光滑映射f:Rm→R,使下面的等式成立：

xt=f(xt-m，xt-m+1，…,xt-1)

那么，我们把m称作嵌入维，而最小嵌入维则是使上式成立的最小的m取值。对时间序列进行预测，就是根据N-m 个Rm中的点Xt=(xt-m，xt-m+1，… ,xt-1)和Yt=xt组成样本对（Xi，Yi），（i=m+1，m+2，…，N），利用这些样本估计映射f，从而给出Xn+1的近似值。

为了降低建模误差，对原始数据首先进行零处理以及数据的归一化，然后根据Takens理论进行相空间重构操作，也就是把一维的时间序列转化成矩阵形式，得出数据间的关联关系，从而能得到尽可能多的信息量。为了使重构的相空间能较充分而细致的反映系统运动特征，恰当的选取嵌入维m的大小是相空间重构的关键。

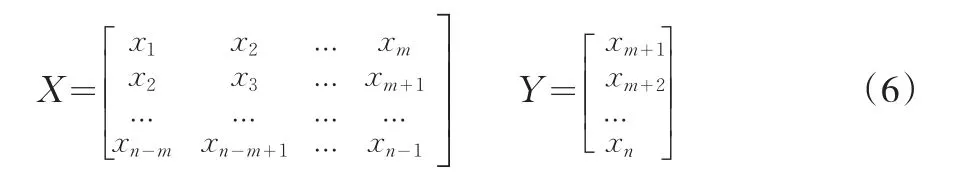
这样，原始的一维时间序列经过变形后可以得到用于预测学习的样本。

2 基于SVMR的模型构建

给定时间序列{xt}，其中xt=x(t),t=1,2,…,N，我们可以把数据分成两部分，一部分用于模型训练，而另一部分则用来测试。其中，我们把前Ntr个数据用来做训练，而后NNtr个数据用来做检验和测试。按照嵌入维数m进行滑动，则可以得到N－m个Rm中的点，也就是Xt={xt－m,xt－m+1,…,xt－1}及其映射值Yt=xt组成的样本对(Xi,Yi),(i=m+1,m+2,...,N),对前Ntr－m个数据进行训练，可以对映射f:Rm→R进行模拟估计，而后N－Ntr个数据则用来做测试，用来对建立的回归模型的预测效果进行检验。根据训练样本建立的SVM回归函数为：

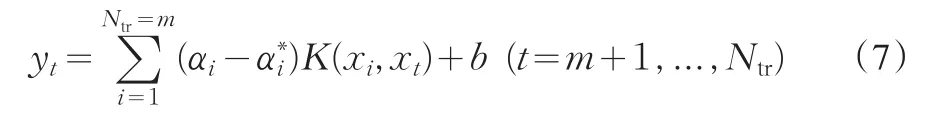
则可以得到一步预测模型为：

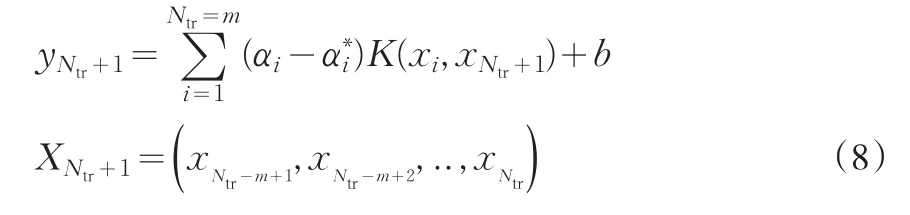
而进一步则L步预测模型为：

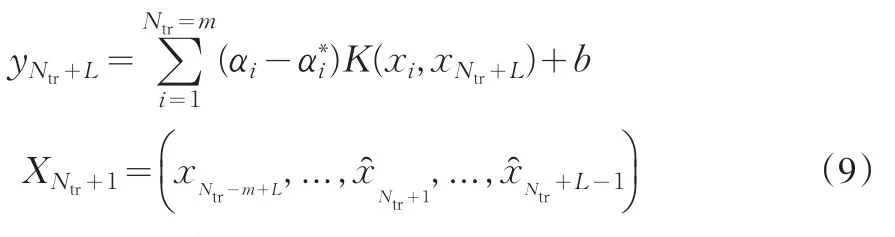
对于以上建立的基于支持向量机回归的时间序列预测模型，首先要确定时间序列嵌入维数m，而m的确定目前尚未完备的理论基础，一般都是通过试验选择使预测误差最小的m，其次就是要确定支持向量机的主要参数，包括核函数形式的确定、模型正则化参数C和回归逼近误差控制参数g。而这些参数一旦确定后，支持向量数也即隐层节点数SV则可以自动确定该预测模型的网络结构，连接权也可由算法自动确定[3]。

对构建的支持向量回归预测模型可以用如下统计量检验其拟合效果和预测。

平均绝对百分误差：

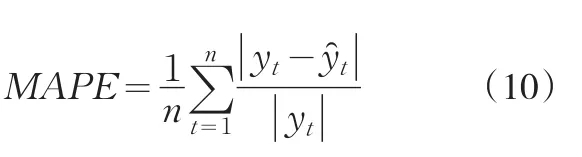
MAPE为相对数，一般而言，在时间序列预测中MAPE的值落在20%-40%就能够满足要求，而在具体分析时，其值越小，说明预测值和实际值越接近，预测模型的精度越高。

3 实证分析

根据前面建立的支持向量机回归预测模型，我们可以对组成房地产预警系统的各项指标的未来值进行短期预测，以武汉市房地产为例利用WEKA软件进行分析，由于组成房地产预警指标体系的指标较多，考虑到篇幅，仅以土地转让面积为例进行预测。

3.1 数据预处理

在用支持向量机回归模型做预测前，必须对指标进行归一化处理，使指标值在[-1 1]内变动,这样使得处理后的数据更容易训练和学习，本文的数据因为在前面进行指标选择时已经进行了处理，所以在这可直接进行试验。

3.2 确定训练样本和测试样本

根据前面分析，要对土地转让面积2010年的增长率进行预测，首先要对增长率进行相间重构，嵌入维数m考虑到数据的个数不多，参考了其他文献[3-4]，在多次实验的基础上，确定为m=4，也就是从第一年开始，前四年作为输入，第五年为输出，接着滑动窗口，从第二年开始，2、3、4、5年作为输入，第六年作为输出，如此循环下去，则共有10组数据。在建模时，为了保证模型的泛化性，把样本分成5份，采用5折交叉验证。

3.3 参数的选择与误差分析

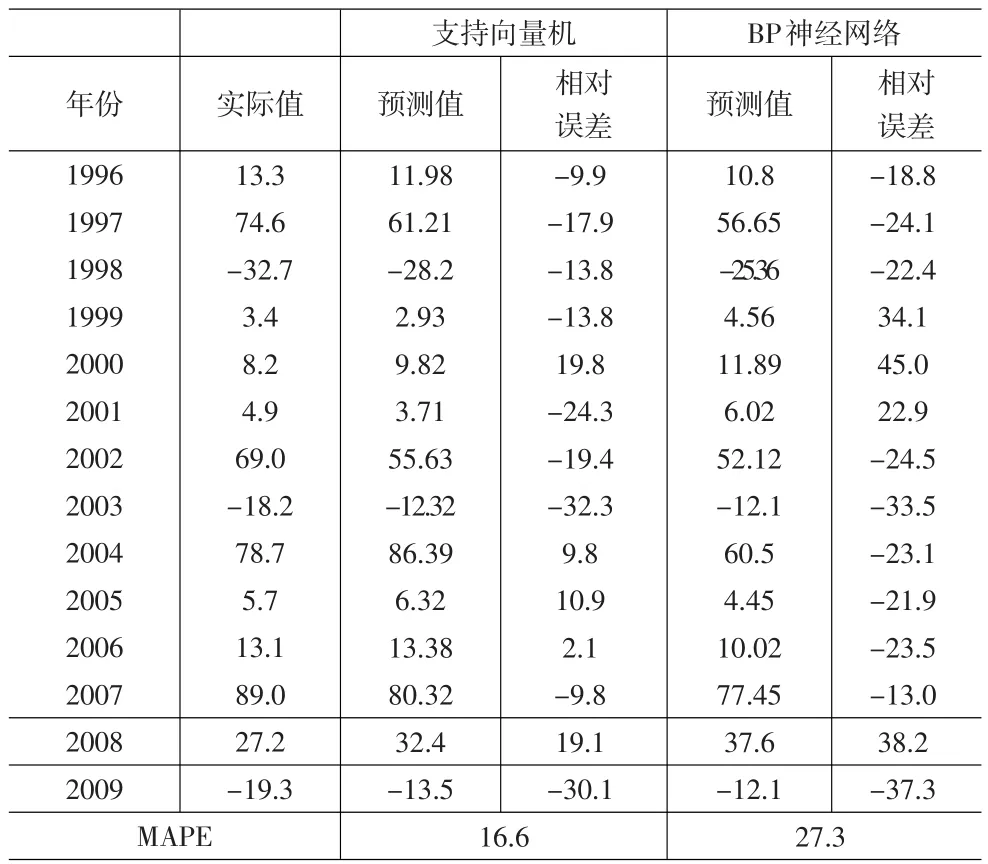
表1 土地转让面积增长率实际值与预测值比较 （%）

对以上10组数据建立模型，RBF函数因其优秀的局部逼近特性在SVM中应用最为广泛，本文的核函数选择RBF函数，经过反复试验，确定C=1，g=0.008，并进行误差分析和检验。我们对同一组数据分别用BP神经网络和支持向量机这两种方法来建立模型，具体比较结果如表1。

3.4 单指标预测

利用支持向量机对已知的历史数据进行学习，建立模型，通过检验满足误差要求后就可以利用建好的模型来对该指标的未来值进行预测，按照同样的格式对数据进行整理，即根据2010年之前的前四年的增长率来推算2010年土地转让面积增长率，支持向量机会根据前面的模型，进行自动学习，得出2010年土地转让面积增长率的值，通过weka软件的运算结果，可得到2010年武汉市土地转让面积增长率为15.6%。

4 研究结论

由预测结果得知,2010年武汉市土地增长率和2009年相比，将会上升，这与武汉市房地产发展的实际相符合，MAPE为16.6%，精度满足预测要求，且精度明显高于BP神经网络,，说明基于支持向量机回归的房地产单指标预测模型表现出了较强的泛化能力,得到令人满意的结果。

[1] Tay FEH,Cao LJ.Application of Support Vector Machines in Financial Forecasting[J].Omega,2001,9(4).

[2] 许建华,张学工,李衍达.支持向量机的新发展[J].控制与决策,2004,

19(5).

[3] 崔万照,朱长纯,保文信星.混沌时间序列的支持向量机测定与预测[J].物理学报,2004,53(10).

[4] 周佩玲等.相空间重构在股票短期预测中的应用[J].中国科学技术大学学报,1999,(29).