基于T-GOWA和T-IGOWA算子的二元语义多属性决策方法
刘 兮,陈华友,周礼刚
(安徽大学 数学科学学院,合肥 230039)
0 引言
自Yager[1]于1988年提出了有序加权平均(OWA)算子后,OWA算子作为一种数据信息集成算子在决策、管理、人工智能、专家系统等诸多领域迅速得到了很广泛的应用。1999年Yager又提出一种诱导有序加权平均(IOWA)算子[2],该算子先是通过诱导变量对数据进行排序,然后加权集成,它是OWA算子的一种推广形式。最近文献[3]提出了一种广义OWA(GOWA)算子,GOWA算子是在OWA算子上增加一个新参数来控制变量值的变化程度,是OWA算子的拓展。文献[4]把GOWA算子拓展到直觉模糊环境,提出了直觉模糊多属性决策问题的GOWA方法。文献[5]将GOWA算子和IOWA算子相结合,提出了诱导广义有序加权平均(IGOWA)算子。
在许多现实决策中,由于问题自身的复杂性和信息的模糊、不确定性,决策者往往难以用定量化的方法来描述决策信息,而一般较好的选择是采用定性的语言形式来表示。需要指出的是,在对决策者的语言评价信息进行集结时,得到的结果往往不能够用预先定义的语言评价集中的元素来准确表达,只能近似的表示出来,这就造成了信息的损失和集结结果的不精确性。为此,西班牙学者Herrera等人于2000年首次提出了关于语言信息集结的二元语义分析方法[6],较好地克服了这类缺陷,同时还提出了基于二元语义有序加权平均(T-OWA)算子,并将其成功应用于多粒度语言信息的多属性决策之中[7]。文献[8]提出了二元语义有序加权几何(T-OWG)算子,分析了T-OWA算子和T-OWG算子的性质。文献[9]提出了二元语义混合加权平均(T-HWA)算子,并指出二元语义加权算术平均(T-WA)算子和T-OWA算子均为T-HWA算子的特例。文献[10]将IOWG算子推广到二元语义中,提出了二元语义诱导有序加权几何(T-IOWG)算子,并分析了其性质,最后提出一种基于T-IOWG算子的二元语义多属性群决策方法。本文把GOWA算子和IGOWA算子拓展到二元语义环境中,提出了二元语义广义有序加权平均(T-GOWA)算子和二元语义诱导广义有序加权平均(T-IGOWA)算子,并探讨了这些算子的一些性质和特例,最后基于这些算子,分别在单人决策和群决策这两种情形下,提出了属性权重已知且属性值为语言信息形式给出的多属性决策方法。实例分析的结果表明该方法是有效的和可行的。
1 主要概念和结论
1.1 二元语义
二元语义是采用一个二元组(sk,ak)来表示语言评价信息的方法,其中元素sk是预先定义好的语言评价集ST中的第k个元素;ak为符号转移值,且满足ak∈[ )-0.5,0.5,表示经过集结计算后得到的语言信息与最贴近元素sk之间的差别。这里ST是由奇数个元素构成的有序语言评价集,即T称为ST的粒度。一般要求ST满足:(1)有序性:当i≥j时,有(2)存在逆运算算子:,其中j=T-i;(3)极大化运算和极小化运算:当时,有
定义1[6,7]若sk∈ST为语言短语,令函数:θ(sk)=(sk,0),sk∈ST,则称θ:ST→ST×[ )-0.5,0.5为语言短语对应的二元语义形式的转换函数。
定义2[6,7]设β∈[0,T-1]为语言评价集ST经某集结方法得到的实数,令:

则称函数 Δ:[0,T-1]→ST×[ )-0.5,0.5为实数β对应的二元语义信息的转换函数,其中round为四舍五入取整算子。
定义3[6,7]设(sk,ak)是一个二元语义信息,sk为ST中第k个元素,ak∈[- 0.5,0.5 ),令 Δ-1(sk,ak)=k+ak=β,则称Δ-1:ST×[- 0.5,0.5)→[0,T-1]为转换函数Δ的逆函数。Δ-1的意义在于把二元语义信息转换为相应的实数。
假设(sk,ak)和(sl,al)为两个二元语义,其序关系满足[6,7]:(1)若k>l,则 (sk,ak)> (sl,al),(2)当k=l时,若ak>al,则(sk,ak)>(sl,al);若ak=al,则(sk,ak)=(sl,al)。
1.2 T-GOWA算子和T-IGOWA算子
定义4[6]设{(s1,a1),(s2,a2),…,(sn,an)}是一组二元语义信息,w=(w1,w2,…,wn)T为相应的权重向量,且:

则称Φ为二元语义加权算术平均(T-WA)算子。特别地,当wj=1/n,j=1,2,…,n时,则算子Φ退化为二元语义算术平均算子。
定义5[6]设{(s1,a1),(s2,a2),…,(sn,an)}是一组二元语义信息,令:

其中(δ(1),δ(2),…,δ(n))是 (1,2,…,n)的一个置换,使得(sδ(j-1),aδ(j-1))≥(sδ(j),aδ(j)),j=2,3,…,n,且:
ω=(ω1,ω2,…,ωn)T是与函数 Ω 相关联的权重向量,,则称Ω为二元语义有序加权平均(T-OWA)算子。
定义6[3]设fω:Rn→R,若:

其中ω=(ω1,ω2,…,ωn)T是与fω相关的加权向量,满足且bj是实数a1,a2,…,an中按从大到小的顺序排列的第j个大的数,参数λ∈(0,+∞),则称函数fω是n维广义有序加权平均算子,简记为GOWA算子。
定义7[5]设为n个二维数组,gω:Rn→R,若:

则称函数gω是由u1,u2,…,un所产生的n维诱导广义有序加权平均算子,简记为IGOWA算子,uj称为aj的诱导值。其中u-index(j)是u1,u2,…,un中按从大到小的顺序排列的第j个大的数所对应的下标,ω=(ω1,ω2,…,ωn)T是与IGOWA算子相关的加权向量,满足j=1,2,…,n,参数λ∈(0,+∞)。
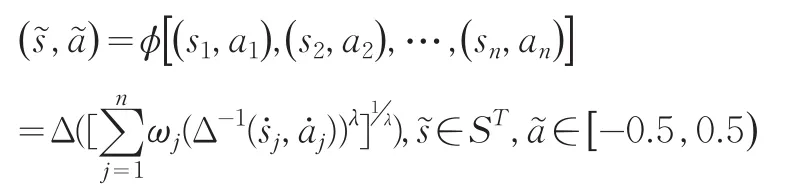
定义8设{(s1,a1),(s2,a2),…,(sn,an)}是一组二元语义信息,若其中ω=(ω1,ω2,…,ωn)T是与函数ϕ相关联的权重向量,,参数λ∈(0,+∞),且是按照序关系确定的(s1,a1),(s2,a2),…,(sn,an)中第j大的元素,则称ϕ为二元语义广义有序加权平均(T-GOWA)算子。
由定义8可得到以下几个结论:
(1)当λ=1 时,有则T-GOWA算子转化为 T-OWA算子;
(2)当λ→0+时,有,则T-GOWA算子转化为 T-OWG算子。

显然,由定义9也可得到以下几个结论:
(1)当λ=1时,有,则T-IGOWA算子转化为T-IOWA算子;
(2)当λ→0+时,有则 T-IGOWA 算子转化为T-IOWG算子。
1.3 T-GOWA算子和T-IGOWA算子的性质
关于T-GOWA算子,具有如下的性质:
性质1(置换不变性)设(s′1,a′1),(s′2,a′2),…,(s′n,a′n)是(s1,a1),(s2,a2),…,(sn,an)的任一置换,那么集结二元语义信息所得结果与集结的先后次序无关,即:

性质2(幂等性)设(s1,a1),(s2,a2),…,(sn,an)是一组二元语义信息,若对∀j,有(sj,aj)=(s,a),则:
ϕ[(s1,a1),(s2,a2),…,(sn,an)]=(s,a)证明:因为对 ∀j,有 (sj,aj)=(s,a),则,则:

性质3(单调性)设(s1,a1),(s2,a2),…,(sn,an)和(s′1,a′1),(s′2,a′2),…,(s′n,a′n)是两组二元语义信息,在权重向量ω不变的情形下,若对 ∀j,有 (sj,aj)≥(s′j,a′j),则:

证明:由于:
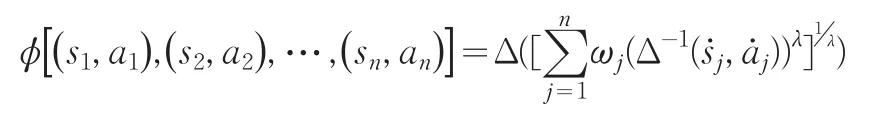
两边取自然对数可得:

再两边对Δ-1(s·j,a·j)求导可得:

又因为对 ∀j,有 (sj,aj)≥(s′j,a′j),可得则
故:

性质4设ϕ为T-GOWA算子,且ϕ=ϕ(λ),λ1≥λ2,则:ϕ(λ1)≥ϕ(λ2)
性质5(有界性)T-GOWA算子介于max算子和min算子之间,即:

故结论成立。
可以证明T-IGOWA算子也存在与T-GOWA算子类似的性质,只是运算法则不同,限于篇幅,这里不再赘述。
2 2T-GOWA算子和T-IGOWA算子的应用
下面基于T-GOWA算子和T-IGOWA算子,对属性权重已知且属性值以二元语义信息形式给出的多属性决策方法进行探讨:
2.1 T-GOWA算子在单人决策的应用
在单人决策的情况下,我们给出一种基于T-GOWA算子的多属性决策方法,具体步骤如下:
步骤1:对于某一多属性决策问题,设A={A1,A2,…,Am}为方案集,G={G1,G2,…,Gn}为属性集,属性权重向量为决策者对方案Ai按照预先定义好的语言评价集…,T-1}}关于属性Gj进行测度,得到属性值rij(rij∈ST),从而构成决策矩阵R=(rij)m×n
步骤2:利用权重向量w和决策矩阵R=(rij)m×n得到加权二元语义决策矩阵,其中
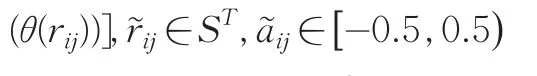
步骤3:利用T-GOWA算子对R按行进行集结,得到各方案的综合属性值

步骤4:根据二元语义的序关系对各方案综合属性值Li(ω)进行方案的排序和选优。
2.2 T-IGOWA算子在群决策的应用
在大型决策或者重要决策的过程中,为体现决策的民主性和合理性,往往需要多个决策者共同参与,下面给出一种基于T-IGOWA算子的多属性群决策方法,具体步骤如下:
步骤1:设A、G分别为方案集和属性集,属性权重向量为,d2,…,dt}为决策者集,τ={τ1,τ2,…,τt}是t位决策者的权重向量,设决策者dk∈D给出方案Ai∈A在属性Gj∈G下的属性值,从而构成决策矩阵
步骤2:利用T-WA算子和权重向量w=[w1,w2,…,wnT]对R(k)中第i行进行集结,得到决策者dk对方案Ai的综合属性值
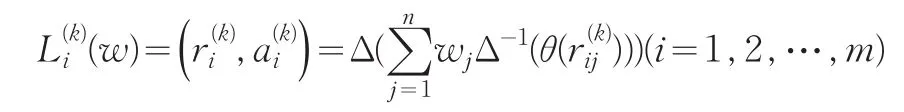
步骤3:利用T-IGOWA算子对t位决策者给出的方案Ai的综合属性值进行集结,得到方案Ai的群体综合属性值

其中 (rτ-index(l),aτ-index(l))是τ1,τ2,…,τt中第l大的元素所对应的二维数组中的第二个分量ω=(ω1,ω2,…,ωt)T是与T-IGOWA算子相关联的权重向量参数λ∈(0,+∞)由决策者根据实际情况预先选择确定。
步骤4:根据二元语义的序关系对各方案综合属性值Li(τ,ω)进行方案的排序和选优。
3 实例分析
某个风险投资公司进行项目投资评估,有4个备选企业Ai(i=1,2,3,4),4个评价属性Gj(j=1,2,3,4)(属性分别为风险因素、成长因素、社会政治影响因素和环境影响因素),属性权重为w=(0 .25,0.3,0.2,0.25)T。该公司聘请三位专家dk(k=1,2,3)参与决策分析,专家权重为τ=(0.3,0.5,0.2),利用语言评价集所得语言评估矩阵为:

下面利用2.2提出的方法进行方案排序:
步骤1:利用T-WA算子和权重向量w=(0.25,0.3,0.2,0.25)T对R(k)中第i行进行集结,得到决策者dk对方案Ai的综合属性值

步骤2:再利用T-IGOWA算子对t位决策者给出的方案Ai的综合属性值进行集结,这里与T-IGOWA算子相关联的权重向量为ω=(0 .3,0.4,0.3)T,专家权重为τ=(0.3,0.5,0.2),得到各方案Ai的群体综合属性值:

当参数λ取一些特殊值时,Ai的群体综合属性值如表1。步骤3:根据二元语义的序关系,得到方案排序如表2。可见最优方案为A4。

表1

表2
4 结束语
本文针对二元语义信息的集结问题,将传统的GOWA算子和IGOWA算子进行拓展,提出了一些新的集结算子:二元语义广义有序加权平均(T-GOWA)算子和二元语义诱导广义有序加权平均(T-IGOWA)算子,探讨了这些算子的性质和特例,并把它们应用于属性权重已知且属性值为语言信息形式给出的多属性决策中。该决策方法不仅充分考虑了各决策者的重要性,而且参数的不同使决策者能够有更宽泛的选择,具有很好的实用价值。
[1] Yager R R.On Ordered Weighted Averaging Aggregation Operators in Multi-criteria Decision Making[J].IEEE Transactions on Systems,Man,and Cybernetics,1988,(18).
[2] Yager R R,Filev D P.Induced Ordered Weighted Averaging Operators[J].IEEE Transactions on Systems,Man,and Cybernetics,1999,(29).
[3] Yager R R.Generalized OWA Aggregation Operators[J].Fuzzy Optimization and Decision Making,2004,(3).
[4] 伍之前,李登峰.基于GOWA算子的直觉模糊多属性决策方法[J].运筹与管理,2010,19(3).
[5] J M Merigo,A M Gil-Lafuente.The Induced Generalized OWA Operator[J].Information Sciences,2009,(179).
[6] Herrera F,Martinez L.A 2-tuple Fuzzy Linguistic Represen-tation Model for Computing with Words[J].IEEE Transactions on Fuzzy Systems,2000,8(12).
[7] Herrera F,Martinez L.A Model Based on Linguistic 2-tuples for Dealing with Multi-granular Hierarchical Linguistic Contexts in Multi-expert Decision-making[J].IEEE Transactions on Systems,Man and Cybernetics,2001,31(2).
[8] 姜艳萍,樊治平.二元语义信息集结算子的性质分析[J].控制与决策,2003,18(6).
[9] 魏峰,刘淳安,刘三阳.基于不确定信息处理的语言群决策方法[J].运筹与管理,2006,15(3).
[10] 卫贵武.基于T-OWG和T-IOWG算子的二元语义多属性群决策方法[J].统计与决策,2008,(10).

