基于蒙特卡罗方法的软土微观结构随机几何模型*

杨锡鎏，周翠英

(中山大学工学院//岩土工程与信息技术研究中心，广东 广州 510275)

基于软土的微观结构特征建立其微观结构仿真模型，对软土的工程力学性状进行数值模拟是当今土力学的前沿课题之一。经过许多学者的研究总结，土体的微观结构主要包括：结构单元体特征、颗粒的排列特征、孔隙性和结构连结4个方面[1]。其中，结构单元体特征和孔隙性是软土微观结构特征中最重要的因素，同时也对软土的工程力学特性起着决定性作用。因此，近年来关于土体微观结构仿真建模方面的研究，主要以结构单元体和孔隙作为仿真对象分为两大类：①以土体中的颗粒或结构单元体为仿真对象，常采用Cundall[2]提出的离散单元法，把土颗粒等效成刚性的圆盘或钢球[3-4]；王功明等[5]则把土壤结构体等效为9种基本粒子，提出了基于粒子系统的土壤可视化仿真模型；②以土体中的孔隙空间为仿真对象，常采用多孔介质的孔隙网络模型[6-7]，用简单的几何形状模拟土体中的孔隙体和孔喉。上述模型主要应用于土体压缩破坏和土体中渗流过程的模拟，但对于同时涉及孔隙水压力消散和土骨架变形的软土排水固结过程，只以结构单元体或孔隙作为单一仿真对象建立的软土微观结构模型，将很难基于软土排水固结过程的微观作用机理进行其微观结构演化的数值模拟。

基于此，本文根据常规土工试验获得的土样孔隙比和各粒组含量百分比，参考混凝土细观结构仿真中的随机骨料模型思想[8]，采用蒙特卡罗方法生成一定数量的随机多边形单元代表软土微观结构中的各类结构单元体和孔隙，然后通过把它们随机分布到给定大小的区域中，建立了软土微观结构的随机几何模型，为进一步实现软土各种工程力学性状的微观数值模拟提供了几何模型的基础。

1 随机多边形单元的生成

在软土的微观结构中，结构单元体和孔隙的大小、形状以及表面特征都是随机的，为了模拟这种随机性，本文采用了随机系统仿真研究中常用的蒙特卡罗方法，产生一系列的随机数作为控制随机多边形单元大小形状的参数，其中包括：多边形的边数n、丰度c和粒径d。多边形的边数n用于控制多边形单元的表面特征，n越小反映多边形单元的表面越呈棱角状越粗糙，n越大反映多边形单元的表面越圆滑；多边形的丰度c是指多边形单元的短轴与长轴之比，该参数用于控制多边形单元的几何形状特征，c越小反映多边形单元越趋于长条形，c越大反映多边形单元越趋于等轴形；多边形的粒径d用于控制多边形单元的尺寸大小。根据雷华阳[9]对饱和软黏土微观结构中关于颗粒与孔隙丰度的定量研究，以及《岩土工程勘察规范》对土体中砂粒和粉粒粒径范围的界定[10]，在各类随机多边形单元的生成过程中，上述各参数按表1所示的取值范围内随机生成。

1.1 单个随机多边形单元的生成

随机生成上述参数n、c、d后，具体的随机多边形单元生成步骤如下：

1) 以原点为中心，将xy平面平均划分为n个区域，在每个区域内随机取一点作为多边形的顶点，如图1所示，该点的坐标表达式为：

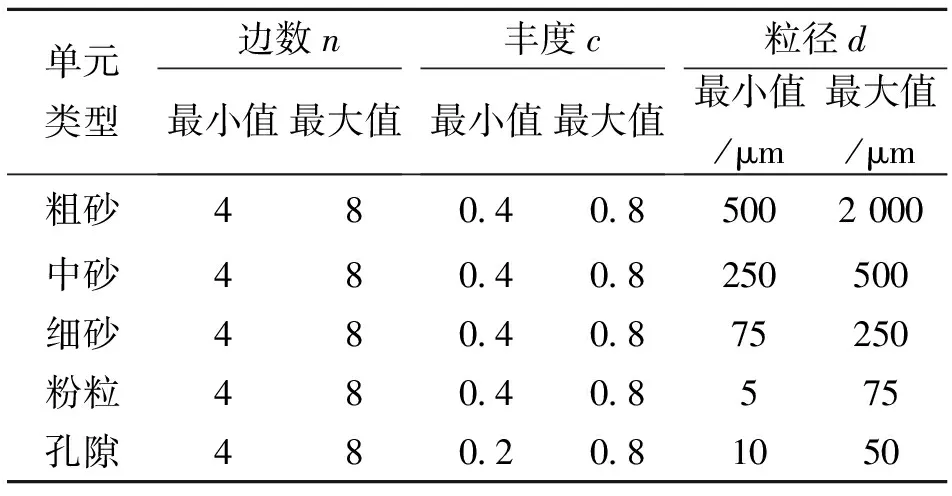
表1 各类多边形单元参数的取值范围

xi=ricos[(2π/n)(i-1)+θi]

(1)

yi=risin[(2π/n)(i-1)+θi]

(2)

其中，i为顶点序号；ri为顶点i所对应的极半径，在[dc/2,d/2]区间内随机生成；θi为顶点i所对应的极角，在[0,2π/n]区间内随机生成。

2) 连接这n个顶点，即可得到一个符合给定参数范围，形状、尺寸和表面特征均为随机的多边形单元。

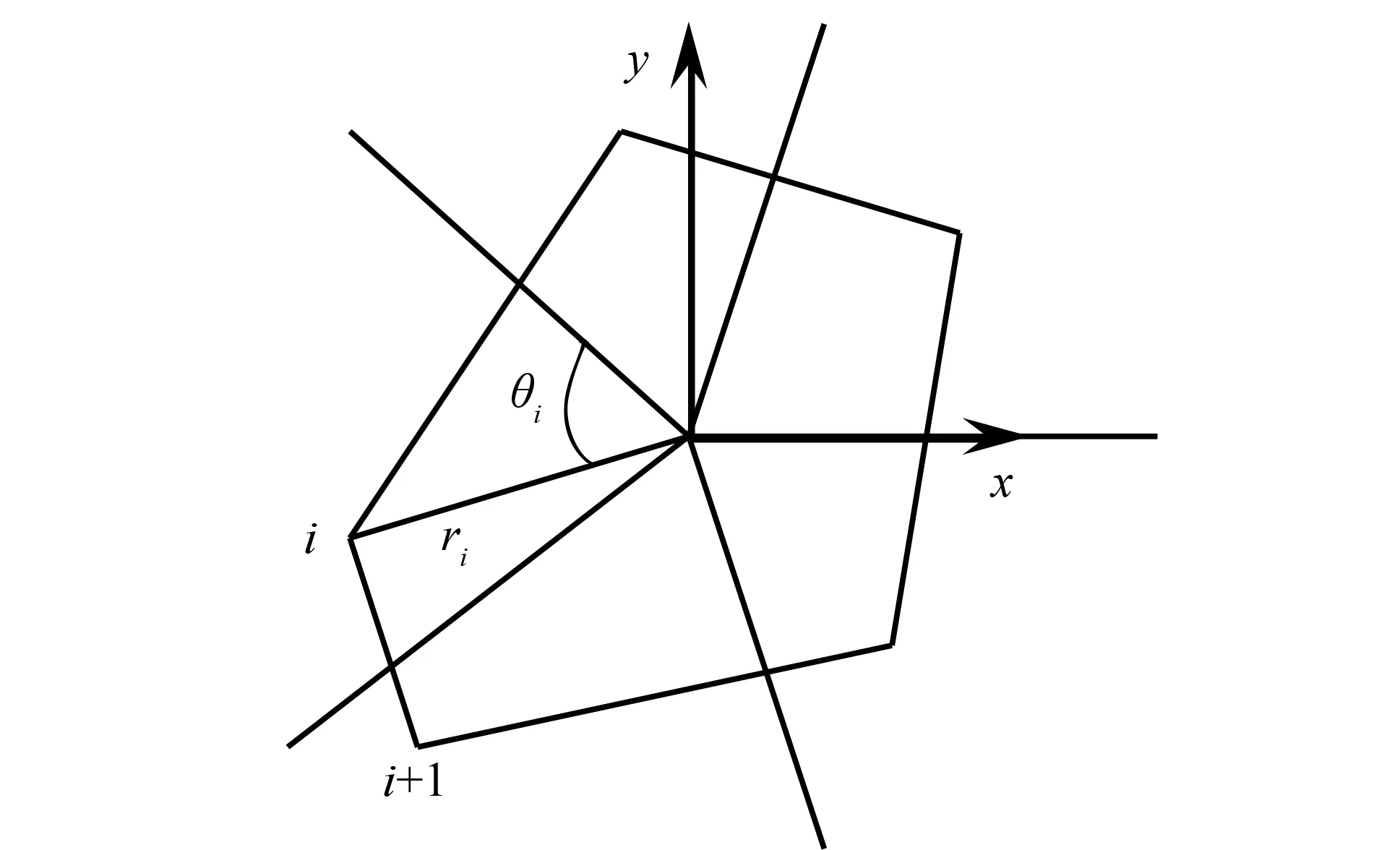
图1 随机多边形单元的生成

1.2 各类随机多边形单元的生成数量控制

在建立软土微观结构的随机几何模型过程中，代表各类结构单元体和孔隙的随机多边形单元数量并不是任意的。本文通过对土样进行常规土工试验获得的孔隙比e和各粒组的含量百分比wt进行控制，这样可以使建立的微观结构仿真模型最大程度地接近实际。具体的控制方法如下：

1) 计算所建立的软土微观结构随机几何模型的总面积A；

2) 根据土样的孔隙比e计算孔隙单元的控制总面积Av：

Av=eA/(1+e)

(3)

3)根据土样中各粒组的含量百分比wt计算各类结构单元体的控制总面积At：

At=Awt/(1+e)

(4)

4)对某一类单元，按前文所述方法生成一个随机多边形单元i，并计算其面积Si；

5) 根据该多边形单元的类型，计算已生成的该类多边形单元的面积之和∑Si；

6) 如果∑Si大于该类单元的控制总面积At则删除最后一次生成的多边形单元，并结束该类多边形单元的生成程序，否则继续执行步骤4)；

7) 对各类随机多边形单元的生成程序分别执行步骤4)～6)。

其中，步骤4)中多边形单元的面积S可用多边形单元的各个顶点与单元中心的连线把多边形单元划分成n个三角形(如图2所示)，再通过累加计算这n个三角形的面积之和求得。由于多边形单元的各个顶点坐标已由公式(1)和公式(2)给出，且多边形单元的中心位于原点，因此三角形的面积SΔ可由以下公式求得：

(5)

其中，SΔi为多边形单元中第i个三角形的面积；xi,yi,xi+1,yi+1分别为多边形单元第i和i+1个顶点的xy坐标。

图2 多边形单元的面积计算

2 多边形单元的随机分布

当生成一定数量的各类随机多边形单元后，就可以把它们随机分布到给定大小的模型区域内来模拟结构单元体和孔隙在软土微观结构中随机分布的特性。以宽为b、高为h的矩形模型区域为例，进行多边形单元随机分布的具体步骤如下：

1) 将已生成的随机多边形单元按其最大极半径的大小进行排列，按从大到小的顺序把多边形单元逐个随机分布到模型区域内。这样能避免进行分布时出现过多的重叠判断或没有足够的空间分布粒径较大单元的情况，从而提高模拟质量和缩短程序运行时间；

2) 逐个分布多边形单元时，首先在模型区域内随机取一点(Ox,Oy)，并把多边形单元的中心平移到该点上，即多边形单元各顶点的坐标修改为：

(6)

(7)

其中，Ox和Oy分别为在区间(rmax，b-rmax)和(rmax，h-rmax)上均匀分布的随机数，rmax为该多边形单元的最大极半径；

3) 判断新分布的多边形单元是否与已分布到模型区域内的多边形单元发生重叠或相交，如果是，则返回步骤2)重新对该多边形单元进行随机分布；否则对下一个多边形单元执行步骤2)和3)，直到所有多边形单元都分布到模型区域内为止。

为了避免某一多边形单元在进行随机分布过程中，多次与已分布的单元发生重叠或相交而不断需要重新分布，导致程序运行时间过长，建议对每个多边形单元的分布失败次数进行记录。当多边形单元随机分布到模型区域后，与已分布的多边形单元发生重叠或相交，需要重新对其进行随机分布时，该单元的分布失败次数累计加1。当某个多边形单元的分布失败次数达到某一程序控制值，如5 000次，则放弃对该多边形单元进行随机分布并将其删除。

3 多边形单元的重叠和相交判断

在上述对多边形单元进行随机分布的过程中，最关键的算法在于判断两个多边形单元是否发生重叠或相交，其判断流程图如图3所示。

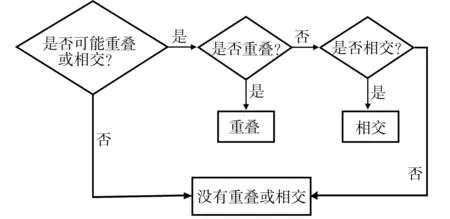
图3 多边形单元重叠或相交的判断流程图

1) 针对流程图中判断两个多边形单元是否可能存在重叠或相交的问题，可以通过计算多边形单元i和j的中心距离是否大于它们的最大极半径之和进行判断，即：

(8)

其中，Oxi、Oyi、Oxj、Oyj分别为多边形单元i和j随机分布后的中心点坐标；rmax i、rmax j分别为多边形单元i和j的最大极半径。

如果多边形单元i和j的中心距离大于它们的最大极半径之和，则它们不可能发生重叠或相交；否则它们有可能重叠或相交，需进行下一步判断。

2) 针对流程图中判断两个多边形单元是否重叠的问题，可以分别对其中一个多边形单元的所有顶点是否全部位于另一个多边形单元的内部进行判断。其核心算法为判断一点是否位于一个多边形单元的内部，按图2所示把多边形单元划分成n个三角形，把问题转化为判断一点是否位于这n个三角形中的其中之一的问题，然后按文献[11]介绍的判断一点是否位于一个三角形内部的方法实现。

3) 针对流程图中判断两个多边形单元是否相交的问题，可以依次对多边形单元i的每条边Lni，遍历多边形单元j的每条边Lnj，判断Lni是否与Lnj相交，如果是则表示两个多边形单元相交；否则，如果多边形单元i的每条边都没有与多边形单元j的任一条边相交，则表示两个多边形单元没有相交。其核心算法为判断两条线段是否相交，可按文献[12]介绍的方法实现。

4 软土微观结构的随机几何模型

基于软土的微观结构是一个由结构单元体、孔隙和结构连结所组成的三相体系，本文通过随机分布一定数量的各类多边形单元到给定大小的区域内来代表软土微观结构中的结构单元体和孔隙，并假设除去结构单元体和孔隙之外的区域为结构连结，从而建立了软土微观结构的随机几何模型。由于软土中结构单元体之间的结构连结主要是以黏土作胶结剂为主的黏质胶结连结以及由黏土畴和有机质集聚在一起形成的链条连结[13]，因此模型中假设结构连结的部分代表软土中的黏粒含量。

基于上述假设和前文介绍的随机多边形单元生成及随机分布方法，本文以Visual C#为开发工具，结合OpenGL图形函数库，编写了软土微观结构的随机几何模型仿真程序。该程序通过输入模型宽度、模型高度、孔隙比以及土样中各粒组的含量百分比作为建模参数。下面根据广东省某高速公路工程试验段软土土样的土工试验结果，按照表2所示的建模参数，分别建立了取土深度为2.5 m和10.8 m两个软土土样在天然状态下的微观结构随机几何模型(如图4所示)，模型的高度和宽度均为100 μm，图中黑色多边形为孔隙单元，白色多边形为各类结构单元体，剩余的白色空间为结构连结。图5为这两个软土土样的实际微观结构扫描电镜图片经过图像二值化处理后的微观结构图像，其中黑色代表孔隙，白色代表土骨架。从图4与图5的对比可以看出，所建立的软土微观结构随机几何模型与土样的实际微观结构图像具有一定的相似程度。

表2 建模参数

图4 不同取土深度软土土样的微观结构随机几何模型

图5 不同取土深度软土土样的微观结构图像

5 结 论

1) 采用蒙特卡罗方法生成了形状、尺寸和表面特征均为随机的多边形单元代表软土微观结构中的各类结构单元体和孔隙，通过把一定数量的各类多边形单元随机分布到给定大小的区域中，建立了软土微观结构的随机几何模型。在建模过程中，提出了各类随机多边形单元生成数量的控制方法，并探讨了进行多边形单元随机分布时，判断多边形单元是否存在重叠或相交的具体流程和核心算法。

2) 以Visual C#为开发工具，结合OpenGL图形函数库，编写了软土微观结构的随机几何模型仿真程序。对广东省某高速公路工程试验段不同取土深度处的软土土样进行微观结构仿真模拟，结果表明：所建立的软土微观结构随机几何模型与土样实际的微观结构图像具有一定的相似度，验证了本文方法的可行性。

3) 本文提出的软土微观结构随机几何模型基于常规土工试验获得的土样孔隙比和各粒组含量百分比建立，所需建模参数较少且容易获取，可控性较强。如果将该模型与有限元方法相结合，就能进一步实现软土各种工程力学性状的微观数值模拟。

参考文献：

[1]周翠英, 牟春梅. 珠江三角洲软土分布及其结构类型划分[J]. 中山大学学报：自然科学版, 2004, 43(6): 81-84.

[2]CUNDALL P A. A computer model for simulating progressive, large-scale movements in blocky rock systems[C]∥Proceedings of the International Symposium on Rock Mechanics, Nancy, France. 1971.

[3]BOHAC J, FEDA J, KUTHAN B. Modeling of grain crushing and debonding[C]∥Proceedings of the Fifteenth International Conference on Soil Mechanics and Geotechnical Engineering, Lisse. Balkema. 2001.

[4]游碧波, 周翠英. 双层堤基条件下管涌逸出的颗粒流模拟[J]. 中山大学学报：自然科学版, 2010, 49(6): 42-48.

[5]王功明, 郭新宇, 赵春江, 等. 基于粒子系统的土壤可视化仿真研究[J]. 农业工程学报, 2008, 24(2): 152-158.

[6]相方园, 王正, 孟祥磊, 等. 基于序列图像的土壤孔隙网络模型构建[J]. 山东农业科学, 2009, 4: 20-23.

[7]吕菲, 刘建立. 孔隙网络模型在土壤水文学中的应用研究进展[J]. 水科学进展, 2007, 18(6): 915-922.

[8]WANG Z M, KWAN A K H, CHAN H C. Mesoscopic study of concrete Ⅰ: generation of random aggregate structure and finite element mesh [J]. Computers and structures, 1999, 70:533-544.

[9]雷华阳. 饱和软黏土固结变形的微结构效应[J]. 水利学报, 2004, 4: 91-95.

[10]中华人民共和国建设部.GB 50021-2001岩土工程勘察规范[S]. 北京: 中国建筑工业出版社, 2009.

[11]杨锡鎏, 周翠英. 基于ANSYS与OpenGL的高速公路结构物仿真建模及三维地层地表修建方法[J]. 岩土力学, 2010, 31(2): 571-576.

[12]李永江, 华一新. 一种快速判断线段相交的方法[J]. 测绘通报, 2003, 7: 30-31.

[13]高国瑞. 近代土质学[M]. 南京: 东南大学出版社, 1990.