两类高斯超几何多项式零点的渐近分布*
周建荣,黄民海,王红勇
(1. 佛山科学技术学院理学院数学系,广东 佛山 528000;2. 肇庆学院数学与信息科学学院,广东 肇庆 526061;3. 南华大学数理学院,湖南 衡阳 421001)
近年来,关于超几何多项式零点渐近行为的研究引起了国内外许多专家学者的广泛兴趣和关注[1-4]。 对此类问题的研究通常有如下几种方法:其一,基于2F1类多项式与经典的 Jacobi 正交多项式的联系,可以获得关于零点位置及其渐近分布等重要信息[5]。 其二,利用经典的复分析方法直接研究超几何多项式零点的渐近行为[6]。 其三,从超几何函数所满足的欧拉积分替换出发,应用鞍点法导出其零点的渐近性质[7-8]。
本文从欧拉积分替换出发,采用经典的复分析方法探讨了超几何多项式2F1(-n,a;b;z)零点的渐近分布,进一步借助于 Pfaff 的恒等公式,得到了2F1(-n,λ;-n+μ;z)零点的渐近行为。此外,应用Mathematic软件,给出了相关定理的直观说明。
1 高斯超几何多项式
高斯超几何函数的定义如下:
(1)
其中
(ν)k=ν(ν+1)(ν+2)…(ν+k-1)=
是Pochhammer符号。当α=-n为负整数时,(1)中的级数退化为一个n次多项式,此多项式称为高斯超几何多项式。
高斯超几何函数有如下欧拉积分替换
(1-t)γ-β-1(1-zt)-αdt,Re{γ}>Re {β}> 0
(2)
选取α=-n,β=a>0并且γ=b>a,则有

(3)
2 零点的渐近分布
以下,我们基于高斯超几何函数的欧拉积分替换(2),采用经典的复分析方法,得到了超几何多项式2F1(-n,a;b;z)零点的渐近分布(定理1),进一步借助于 Pfaff 的恒等公式 (13),得到了2F1(-n,λ;-n+μ;z)零点的渐近行为(定理2)。
定理1 对任意常数b>a>0,超几何多项式2F1(-n,a;b;z)的零点渐近分布于如下曲线|z-1|=1,n→∞。(如图1)

图和的零点及渐近曲线(x-1)2+y2=1
证明为了讨论2F1(-n,a;b;z) 零点的渐近行为,需先得到如下积分的渐近展开式


(4)
其中f(t)=1-zt。令

(5)

首先计算I1(z),作变量替换r=1-zt,从而有
(6)
由于
(z-1+r)b-a-1=zb-a-1·
从而,I1(z)有如下渐近展开式
(7)

(8)
由于
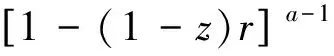
因此,I2(z)的渐近展开式为
(9)
由(3)-(5)式,可知2F1(-n,a;b;z)的每一个零点均满足
I1(z)+I2(z)=0
(10)
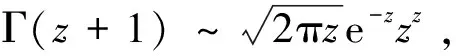
(11)
式(11)两边取模并且开n次方,容易得出,当n→∞时,
|z-1|=1
(12)
引理1 (Enestrom-Kakeya Theorem[9]136) 若0 为了方便起见,我们将用到如下的 Pfaff 恒等公式[10] 2F1(-n,α;-n+1+α-β;1-z) (13) 定理2 对任意的常数λ>0且μ<1,超几何多项式2F1(-n,λ;-n+μ;z)的零点渐近分布于单位圆周: |z|=1。而且当0<μ<1,λ>1时,其所有零点均在单位圆盘: |z|<1之内;当μ<0,0<λ<1时,其所有零点均在单位圆盘:|z|<1之外(如图2)。 图和的零点及渐近曲线x2+y2=1 证明式(13)的左边令α=λ,β=-n+μ可得 (14) (15) (16) 由(14)式和定理2,容易得出如下推论。 推论1 (i)当1 (ii)当0 参考文献: [1]DRIVER K, JORDAAN K. Separation theorems for the zeros of certain hypergeometric polynomials [J]. J Comput Appl Math, 2007, 199: 48-55. [2]DRIVER K, JORDAAN K. Pólya frequency sequences and real zeros of some3F2polynomials [J]. J Math Anal Appl, 2007, 332: 1045-1055. [4]DOMINICI D, DRIVER K, JORDAAN K. Polynomial solutions of differential-difference equations [J]J Approx Theory,2011 163:41-48 [5]DRIVER K, DUREN P. Zeros of the hypergeometricpolynomialsF(-n,b;2b;z) [J]. Indag Math (New Ser), 2000, 11: 43-51. [6]DRIVER K, MÖLLER M. Zeros of the hypergeometric polynomialsF(-n,b;-2n;z) [J]. J Approx Theory, 2001, 110: 74-87. [7]BOGGS K, DUREN P. Zeros of hypergeometric functions [J]. Comput Methods Funct Theory, 2001, 1: 275-287. [8]DUREN P, GUILLOU B J. Asymptotic properties of zeros of hypergeometric polynomials [J]. J Approx Theory, 2001, 111: 329-343. [9]MARDEN M. Geometry of polynomials [M]. American Mathematical Society, Providence, Rhode Island, 1996. [10]ANDREWS G, ASKEY R, ROY R. Special function,encyclopedia of mathematics and its applications [M]. Cambridge: Cambridge University Press, 1999.




