带转移机制且股票价格服从几何Levy过程的连续时间均值-方差投资组合选择*

伍慧玲，李仲飞

(1. 中山大学数学与计算科学学院，广东 广州 510275；2. 中山大学岭南(大学)学院，广东 广州 510275)

1952年，Markowitz[1]提出了单期的均值-方差模型，为现代投资组合选择问题奠定了理论基础并吸引了大量的学者对此进行推广和研究[2-5]。最近几年，带转移机制的连续时间均值-方差模型成为了人们的一个研究热点，在带转移机制的模型里，主要的参数，比如无风险利率，股票的收益率和扩散系数等均与所处的市场状态有关。对于带转移机制的均值-方差模型的研究，有兴趣的读者可以参考文献[6-9]。然而现有的带转移机制的均值-方差模型总是假设股票的价格服从几何布朗运动，具有连续的路径。但在现实中，股票的价格往往会发生跳跃，有兴趣的读者也可参考文献[10-11]。总的来说，对股票价格带跳的均值-方差模型的研究甚少。出于现实的考虑，本文研究了股票价格服从几何Levy过程的均值-方差模型，其中漂移率、波动率和Levy测度均依赖于所处的市场状态。据我们所知，目前还没有文献做过这方面的研究。

1 模型描述

令(Ω，F，P)是一个完备概率空间，{W(t)=(W1(t)，…，Wn(t))T，t≥0}是定义在(Ω，F，P)上的一个n维标准布朗运动。假设市场上有n+1个资产，资产在t时刻的收益与当时所处的市场状态a(t)有关。 其中{a(t)，t≥0}是定义在(Ω，F，P)上的连续时间平稳马氏过程且与{W(t)，t≥0}相互独立，状态空间为S={1，2，…，L}，转移率矩阵为Q=(qij)。 第0个资产为无风险资产，其价格过程是dP0(t)=P0(t)r0(t，a(t))dt，初始化条件P0(0)=P0。第k(k=1，…，n)个风险资产(股票)的价格服从几何Levy过程，即

dPk(t)=Pk(t)[μk(t，a(t))dt+

初始化条件PK(0)=PK>0

u(t)=(u1(t)，u2(t)，…，un(t))T,

r0(t，i)，…，μn(t，i)-r0(t,i))T0,

和σ(t，i)=(σkl(t，i))k，l=1，2，…，n

则在t时刻的财富X(t)满足

(1)

假设投资者的目标是求解优化问题

其中T是投资者考虑的投资期限，d是投资者设定的预期终端财富目标。

我们先用拉格朗日法，引入拉格朗日乘子λ，来解决无约束问题

上述两个问题的最优目标函数及最优策略的关系由下面的引理1给出。

注意到，求解PL(λ，d)等价于求解问题

令

a(t)=i,X(t)=x]

(2)

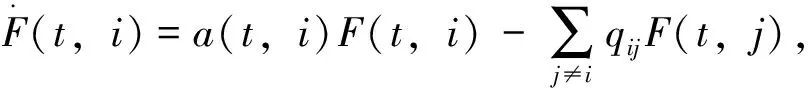
定理1[12](核验定理)

定义算子

令w(t，x，i)∈C1，2，i∈S是下面方程

w(T，x，i)=(x+λ-d)2

(3)

w(t，x，i)=P(t，i)x2+2(λ-d)H(t，i)x+

(λ-d)2G(t，i)

(4)

再将(4)代回(3)，整理出关于x(t)的二次多项式，最后令x2(t)，x(t)的系数和常数项为0，得到P(t，i)，H(t，i)，G(t，i)分别满足下列微分方程

(5)

(6)

(7)

其中，

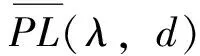
J(0，x0，i0)=P(0，i0)(x0)2+

2(λ-d)H(0，i0)x0+(λ-d)2G(0，i0)

(8)

问题PL(λ，d)最优目标函数为

g(λ)=P(0，i0)(x0)2+2(λ-d)H(0，i0)x0+

(λ-d)2G(0，i0)-λ2

(9)

3 问题P(d)的最优目标函数与最优策略

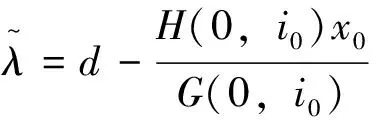
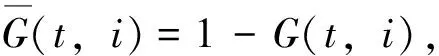
(10)

此时原问题P(d)的最优策略是

将(10)代入(9)简化后可得问题P(d)的最优目标函数和有效前沿为

参考文献：

[1] MARKOWITZ H. Portfolio selection [J]. The Journal of Finance, 1952, 7: 77-91.

[2] LI D, NG W L. Optimal dynamic portfolio selection: multiperiod mean-variance formulation [J]. Mathematical Finance, 2000, 10: 387-406.

[3] ZHOU X Y, LI D. Continuous-time mean-variance portfolio selection: a stochastic LQ framework [J]. Applied Mathematics and Optimization, 2000, 42: 19-33.

[4] CHIU M C, LI D. Asset and liability management under a continuous-time mean-variance optimization framework [J]. Insurance: Mathematics and Economics, 2006, 39: 330-355.

[5] XIE S X, LI Z F, WANG S Y. Continuous-time portfolio selection with liability: mean-variance model and stochastic LQ approach [J]. Insurance: Mathematics and Economics, 2008, 42: 943-953.

[6] YIN G, ZHOU X Y. Markowitz’s mean-variance portfolio selection with regime switching: from discrete-time to their continuous-time limits [J]. IEEE Transactions on Automatic Control, 2004, 49: 349-360.

[7] ZHOU X Y,YIN G.Markowitz’s mean-variance portfolio selection with regime switching: a continuous-time model [J]. SIAM J Control OPTIM, 2003, 42(4): 1466-1482.

[8] CHEN P, YANG H L, YIN G. Markowitz’s mean-variance asset-liability management with regime switching: a continuous-time model [J]. Insurance: Mathematics and Economics, 2008, 43: 456-465.

[9] XIE S X. Continuous-time mean-variance portfolio selection with liability and regime switching [J]. Insurance: Mathematics and Economics, 2009, 45: 148-155.

[10] ØKSENDAL B, SULEM A. Applied stochastic control of jump diffusions [M]. New York: Springer-Verlag Berlin Heidelberg, 2005.

[11] GUO W J, XU C. Optimal portfolio selection when stock prices follow a jump diffusion process [J]. Mathematical Methods of Operations Research, 2004, 60(3): 485-496.

[12] FLEMING W H, SONER H M. Controlled Markov processes and viscosity solutions [M]. New York: Springer-Verlag Berlin Heidelberg, 1993: 163-164.