基于改进遗传算法的非线性方程组求解*

燕乐纬，陈树辉

(1.广州大学工程力学系,广东 广州 510006;2.中山大学应用力学与工程系，广东 广州 510275 )

从理论研究和工程实践中提取出来的数学模型，经常会涉及到非线性方程组。在特解问题中，需要求解非线性方程组以得到满足全部方程的解。在优化问题中，非线性方程则作为等式约束出现。

一般而言，非线性方程组的解析解很难得到。数值方法中，常用的迭代求根方法有牛顿法、拟牛顿法、二分法、割线法等[1]。这些方法共同的缺点是：①对方程本身有较强的限制性要求，如连续、可导、高阶可导等；②对初值比较敏感，一般都要求有相当精度的根的近似值作为初值，初值选得不好时有可能会导致求解失败；③缺乏通用性，有的算法只能求实根，有的算法对重根收敛很慢。

为解决以上问题，一些研究者提出了将非线性方程组转化为优化问题求解的构想。基于这一构想，一些行之有效的优化方法被用来求解非线性方程组，其中遗传算法的使用最为广泛。

遗传算法(Genetic Algorithm，简称GA)是模拟自然界生物进化过程的计算模型，它的求解过程只用到优化问题的目标函数值而不涉及到连续、可导等条件[2]。作为一种随机搜索方法，遗传算法可以从任意初值开始搜索，并能够依概率收敛到全局最优解[3]。此外，遗传算法固有的隐含并行性使它能够同时对参数空间的多个区域进行并行搜索，便于找到非线性方程组所有的解[4]。这些优点使遗传算法在非线性方程组求解中得到了广泛的应用。

但是，标准遗传算法(Standard Genetic Algorithm，简称SGA)本身存在收敛速度慢，局部搜索能力不强的问题。数值试验表明，SGA能够很快定位到最优解所在区域，但其后的收敛速度明显放慢。针对这一问题，遗传算法与局部搜索算子相结合的方法应运而生[5-6]。其基本思想是：先用遗传算法进行全局搜索，得到非线性方程组的一组近似解，再用这组近似解作为局部搜索算子的初值进行精细搜索，最终得到优化问题的全局最优解，也即非线性方程组的根。这一方法的优点是充分利用了遗传算法的全局搜索能力强的优势，并用局部搜索算子弥补了遗传算法局部搜索能力的不足；缺点则是所使用的局部搜索方法(如牛顿法和拟牛顿法)常常需要用到非线性方程组的导数信息，这与遗传算法只需要知道目标函数值就能求解的特性相悖，从而限制了其通用性。

本文在作者以往工作的基础上[7-8]，设计了一种专门用于求解非线性方程组的改进遗传算法。这一改进遗传算法运用了多种宏观策略和微观策略，使之在保持标准遗传算法仅利用函数值信息即可求解这一优点的基础上，提高了局部搜索能力，加快了收敛速度，并有效防止了早熟收敛。

1 问题描述

含有n个未知数，由N个方程组成的实函数非线性方程组的一般形式为

(1)

求解此方程组等价于求解以下极值问题

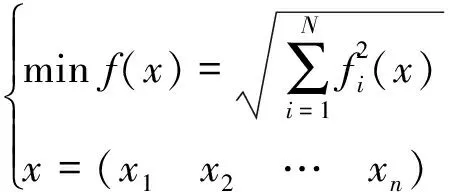
(2)

当f(x)的最小值为0时，所对应的x即为方程组(1)的解。当f(x)的最小值不为0时，方程组(1)无解。这样就将非线性方程组的求解转化成了一个优化问题。

2 改进的遗传算法

2.1 算法要点

2.1.1 宏观遗传策略 为保证解的精度，本文采用实数数组对设计变量进行编码。此外，优化过程中采用了被大量实践证明能够有效提高收敛速度、抑制早熟收敛的种群隔离机制，并利用自适应随机变异算子和算术杂交算子随繁殖代数收缩取值范围的特性实现了遗传算法从渐进阶段向骤变阶段的逐渐转换。

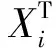
(3)

(4)

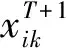
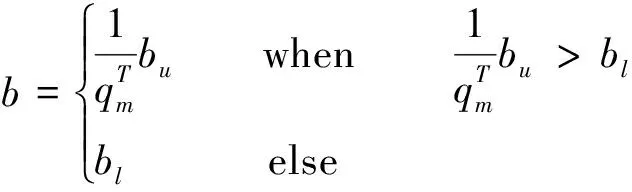
(5)

式中T是当前繁殖代数，bl和bu分别是取值半径b的下界和上界。qm是这一非均匀变异算子引入的一个用于调整变异半径b的收缩速度的参数，其取值范围在1.1～2.0之间。

(5)式使这一变异算子具备了自适应变焦的能力。随着循环次数的增长，变异半径逐渐收缩。在优化的渐进阶段，变异范围较大，变异算子参与全局搜索，目的是快速锁定最优解所在区域；在优化的骤变阶段，变异范围缩小，变异算子用于执行局部精细搜索，目的是准确地确定最优解。设定最小变异范围bl的目的是防止骤变阶段变异算子因变异范围缩得太小而失去意义。

2.2 异种机制

算术杂交算子和自适应随机变异算子的实质都是根据从优化过程中反馈回来的适应度信息，不断缩小搜索范围，进而求得最优解。这有利于算法的迅速收敛，但也增大了近亲繁殖发生的概率。为解决这一问题，本文引入了异种机制来修改广义遗传算法程序，以防止早熟收敛，提高收敛效率。

异种机制的作用机理是：① 对优化过程进行监测，如果发现当前种群发生了近亲繁殖，则启动异种机制；② 在缩小了的搜索范围之外选择数个异种，用以代替现有种群中适应度较低的个体；③ 用带有异种的现有种群生成子代，进入下一次循环。

异种机制的实质是在遗传优化过程中，以较小的概率继续选择种子进入种群，以保证种群的多样性。启动异种机制的概率与当前繁殖代数和种群中近亲繁殖的程度有关。需要指出的是，当种群中有大量的个体发生近亲繁殖时，往往只按很小的比例选择几个异种进入种群。在遗传优化过程中，如果人工干预的强度过大，就会破坏种群结构的稳定性，使遗传算法丧失自身固有的优点，这将是得不偿失的。

2.3 近亲繁殖判别式

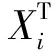
(6)

如果p(T)大于算法给定的近亲繁殖判据pb，则认为第T代种群发生了近亲繁殖。(6)式即本文引入的近亲繁殖判别式。

从近亲繁殖判别式的判别方法可以看出，在本文的研究中，种群内少数个体相互靠近是允许的，也是不可避免的。但如果发生了较多个体集中于一个或几个取值点附近的情况，则有必要启动异种机制进行干预。这是符合人工控制物种杂交优化的规律的。在进化过程的渐进阶段和骤变阶段，判定近亲繁殖的标准应该有所不同。本文所用的临界距离dr是繁殖代数T的变量，这样就实现了异种机制的自适应变焦。

2.4 异种的选取

异种的选取方法有两种：一种是不考虑近亲繁殖本身的特点，在编码空间内完全随机地选择异种的方法；另一种则是考虑近亲繁殖发生的特点，根据近亲繁殖的趋势在近亲繁殖个体所在的邻域内选择异种的方法。前一种方法近似于选择初始种群，有利于提高种群的多样性；后一种方法则是在判断适应度函数爬山方向的基础上进行有向选种，往往能够提高收敛效率。总之二者的目的都是选择与当前种群基因差异较大而适应度较高的个体进入种群，以引发良性链式反应。

3 算 例

3.1 数学模型

文献[9]提出了一种基于三维应力分析确定钢筋混凝土配筋方案的方法。对于钢筋混凝土内任意一点给定的应力张量

(7)

x、y、z方向的配筋率ρx、ρy、ρz可以由下面的12个方程确定。

平衡方程

(8)

(9)

(10)

τxy=σ1xy+σ2mxmy+σ3nxny

(11)

τxz=σ1xz+σ2mxmz+σ3nxnz

(12)

τyz=σ1yz+σ2mymz+σ3nynz

(13)

式中，σ1、σ2和σ3为配筋后应力张量的三个主应力。对应于这三个主应力的方向余弦(x,mx,nx)，(y,my,ny)和(z,mz,nz)需要满足的几何方程是

(14)

(15)

(16)

xy+mxmy+nxny=0

(17)

xz+mxmz+nxnz=0

(18)

yz+mymz+nynz=0

(19)

这12个方程中总共含有15个未知数，即ρx，ρy，ρz，σ1、σ2、σ3、lx、mx、nx、ly、my、ny、lz、mz和nz。其中主应力σ1、σ2、σ3的取值范围是

σ∈[0,fc]

(20)

式中，fc是所用混凝土的抗压强度。

今要求根据以上12个方程求得最小总配筋率，即

minρtotal=|ρx|+|ρy|+|ρz|

(21)

文献[9]通过研究几何方程的特性，尽可能缩小了各方向余弦的取值范围，并采用trial-and-error方法(试错法)得了到一系列的可行解及其对应的总配筋率。比较这些可行解的总配筋率，将最小的一个作为这一优化问题的最优解输出，优化问题就得到了求解。如果试算得到的可行解数量足够多的话，用这一方法得到的解是可以接受的。

但是，这类试错法存在的问题在于:①收敛性无法保证；②在目标函数值较差的地方盲目试错会浪费绝大部分试错机会；③如果试错次数太少，可能得不到足够精确的解。

3.2 优化策略

本文采用前述的改进遗传算法对这一问题进行求解。取lx、my和nz为优化问题的设计变量，它们给定的一组取值就是遗传优化问题的一个个体。对于任意个体(lx0my0nz0)，先将其代入几何方程中，求解出其余的6个方向余弦值mx0、nx0、ly0、ny0、lz0和mz0。然后将全部的方向余弦值代入平衡方程，使之退化为只含有6个未知数(ρx，ρy，ρz，σ1、σ2和σ3)的线性方程组。从这一线性方程组中解出ρx0，ρy0，ρz0，则对应于个体(lx0my0nz0)的适应度是

(22)

这样，对每一个个体，都有一个确定的适应度与之对应。需要指出的是，对给定的个体(lx0my0nz0)，由于几何方程是非线性方程组，会得到多组不同的方向余弦解。实际求解过程中，将这些方向余弦解分别代入平衡方程，计算其适应度，取满足全部约束条件，且适应度最高的一组作为对应于个体(lx0my0nz0)的可行解，并将其适应度作为个体(lx0my0nz0)的适应度输出。

找到了适应度的计算方法，就可以用遗传算法程序对上面的优化问题进行求解了。但是，将个体(lx0my0nz0)的取值代入几何方程求解时，由于几何方程是一个非线性方程组，求解存在一定困难。为解决这一问题，本文在优化问题的大循环中嵌入一个专门用于求解几何方程的嵌套遗传算法循环。内嵌遗传算法的适应度函数依照(2)式构造

(23)

当g2(lx,my,nz)取得最大值1时，所得到的最优解是优化问题的可行解。当g2(lx,my,nz)取不到最大值1时，几何方程无解。此时可令当前个体对应的适应度g1(lx0,my0,nz0)取一个很小的正数，比如10-6，表示其适应度极低，在遗传操作时不予考虑。

此外，根据方程(14)、(15)和(16)可知，设计变量lx、my和nz的取值范围都在[-1,1]区间内。将求解空间分成大小相同的四个区域，在这四个独立的区域内独立同步地进行遗传优化，这样就实现了种群隔离机制。

3.3 算法流程

上述求解过程的遗传算法程序流程如下：

1)将搜索空间划分为四个大小相同的子域，下面的步骤是在每个子域中独立同步进行的；

2)初始化算法中涉及到的所有变量；

3)随机选取lx、my和nz的多组值作为初始种群；

4)随机选择种群中的一半个体进行算术杂交；

5)用选择算子对杂交生成的子代和父代进行选择，保留其中一半的优良个体，与未参与杂交的另一半父代共同组成中间种群；

6)在中间种群中随机选择一半个体进行自适应随机变异；

7)用选择算子对变异生成的子代和父代进行选择，保留其中一半的优良个体，与未参与变异的另一半父代共同组成新一代种群；

8)判断选择得到的种群是否发生了近亲繁殖，如果满足近亲繁殖条件，则启动异种机制，如果不满足，则直接进入下一步；

9)计算种群中每个个体的适应度；如果连续p代种群中的最优个体保持不变，则认为算法已经收敛，满足循环终止条件，进入第10)步；否则，回到第4)步。

10)比较各个子域中得到的最优群体的适应度，选择各子域中适应度最高的个体组成全局最优群体。

11)终止程序，结束遗传优化过程。

内嵌遗传算法的程序流程与上述过程类似，不再赘述。

3.4 计算结果及分析

表1给出了12组不同的应力张量。表2是文献[9]、[10]的计算结果和本文计算结果的对比。其中文献[10]的计算结果是通过三向应力摩尔圆分析得到的。

表1 12组应力张量

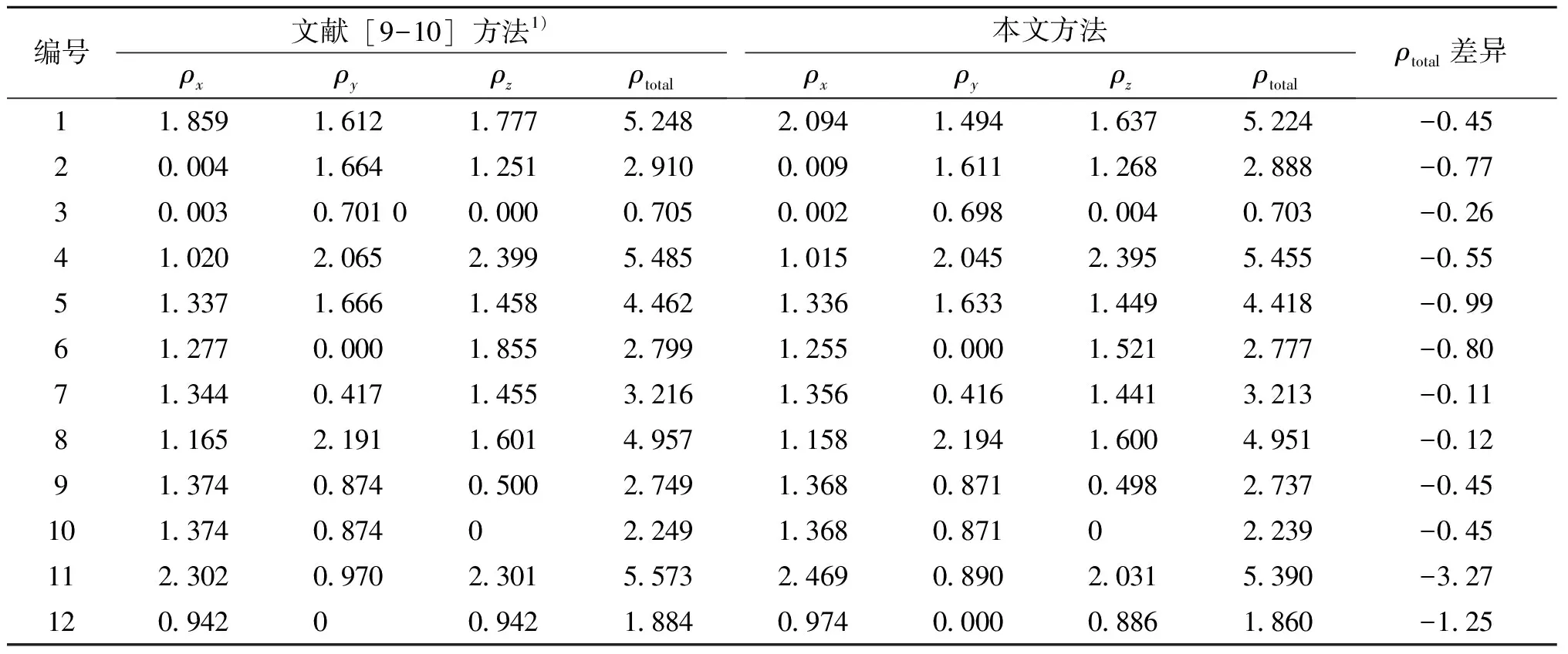
表2 几种计算方法的对比

1)1-10为文献[9]方法，11-12为文献[10]方法

从表2可以看出，本文提出的改进遗传算法不仅能够求解非线性方程组，而且能够求解以非线性方程为等式约束的最优化问题。本文方法得出的结果较文献[9-10]为好，是因为采用了最优保持策略的改进遗传算法能以概率收敛到优化问题的最优解，而文献[9-10]所用的方法不具备这种收敛性。

为了考察异种机制的有效性，本文用含有异种机制和剔除异种机制的遗传算法分别对以上12组算例进行了计算。计算结果表明，含有异种机制的遗传算法平均运行12.6个循环就会收敛；而剔除了异种机制的遗传算法平均运行22.8个循环才收敛。从最优解来看，含有异种机制的遗传算法得到的解均优于剔除了异种机制的遗传算法。这说明异种机制在提高算法收敛速度的同时，还增强了算法的局部搜索能力。

4 结 论

本文采用种群隔离机制、最优保持策略、算术杂交、自适应随机变异和异种机制对实数编码遗传算法进行了改进，在保持遗传算法仅需目标函数值信息即可求解这一优点的基础上，增强了算法的局部搜索能力。将这一改进的遗传算法应用于非线性方程组的求解。数值算例表明，该方法不仅能够求解复杂的非线性方程组，而且能够求解以非线性方程为等式约束的最优化问题。此外，异种机制的引入加快了遗传算法的收敛效率，有效提高了遗传算法收敛于全局最优解的概率。

参考文献：

[1] 陈子仪，康立山，胡欣.遗传算法在方程求根中的应用[J].武汉大学学报,1998, 4(5): 577-580.

[2] HOLLAND J H. Adaptation in natural and artificial systems [M]. Ann Arbor, Michigan: University of Michigan Press, 1975.

[3] WHITELY L D. Deception, dominance and implicit parallelism in genetic search [M]. Annals of Mathematics and Artificial Intelligence, 1992.

[4] GOLDBERG D E. Genetic algorithm in search, optimization and machine learning [M]. MA: Addison-Wesley Publishing Company, 1989.

[5] 罗亚中，周黎妮，唐国金. 遗传算法求解非线性方程组的应用研究[J]. 华南理工大学学报, 2003, 31(7): 140-142.

[6] 胡小兵，吴树范，江驹. 一种基于遗传算法的求代数方程组数值解的新方法[J]. 控制理论与应用, 2002, 19(4): 567-570.

[7] 燕乐纬，蹇开林，黄晓刚. 基于广义遗传算法的结构动力响应优化[J]. 工程力学, 2008, 25(7): 57-65.

[8] 蹇开林，燕乐纬，朱学旺. 基于遗传算法的结构支撑位置优化[J]. 应用力学学报, 2007, 24(1): 306-309.

[9] LAW C W, CHENG Y M, SU R K L. Approach for reinforcement design in reinforced concrete structures based on 3-dimensional stress field [J]. The Hong Kong Institution of Engineers Transactions,2007, 14(2): 1-18.

[10] FOSTER S J, MARTI P, MOJSILOVIC N. Design of reinforced concrete solids using stress analysis [J]. ACI Structural Journal, 2003, 100(6): 758-764.