一种基于GPS单差模型的姿态解算算法

秦红磊，陈万通，金 天，丛 丽

(北京航空航天大学电子信息工程学院，100191北京，qhlmmm@sina．com)

一种基于GPS单差模型的姿态解算算法

秦红磊，陈万通，金 天，丛 丽

(北京航空航天大学电子信息工程学院，100191北京，qhlmmm@sina．com)

针对采用双差模型无法克服双差观测量的强相关性这一问题，以观测量不相关的单差模型为基础，提出一种可递归处理的定姿算法．该方法用码观测量辅助载波相位观测值，增加了信息量，通过递归估计模糊度浮点解及其方差协方差矩阵，从而可以利用LAMBDA算法估计整周模糊度．该算法计算量较小，且具有数值稳定性．实验结果表明，该算法的初始化时间仅占双差模型所用时间的1/50左右．该算法可以有效缩短初始化阶段，能够高效地用于动态姿态解算．

全球定位系统;姿态解算;整周模糊度;短基线

全球定位系统(GPS)具有全球性、全天候和连续的精密三维定位能力．应用GPS载波相位测量技术来确定载体姿态，因具有精度高、长期稳定的准确性、低成本和低能量耗损等优点而日益成为导航领域研究的热点［1］．但由于载波是一种周期性的正弦信号，进行相位测量时存在未知的整周模糊度问题，必须先求得初始时刻的整周模糊度，才能获得高精度的基线坐标［2］．采用双差载波相位观测方程能够有效地减小电离层和对流层误差、轨道误差、卫星和接收机时钟误差，是姿态测量中通常使用的基本模型［3］．静态情况下，基线坐标在任何时刻保持不变，可以利用最小二乘求解浮点解和LAMBDA算法估计初始整周模糊度;动态情况下，基线坐标在不同时刻都对应着不同的未知量，经典最小二乘法和LAMBDA算法不能直接应用，而采用“直接收敛法”由于双差观测量的强相关性，通常会有十几分钟的初始化时间，不利于实际姿态测量应用．

本文避开双差模型，采用观测量不相关的单差模型，递归求解模糊度浮点解及其方差协方差矩阵，使得可以应用LAMBDA算法进行整周模糊度估计，并在有约束条件的情况下，通过扩大候选值空间后再利用约束条件“识别”模糊度的方法，将初始化时间缩减至十几秒，并给出了详细的算法步骤和相应的实验对比．

1 基本观测方程

1.1 码观测方程

接收机s对卫星i的码观测方程为

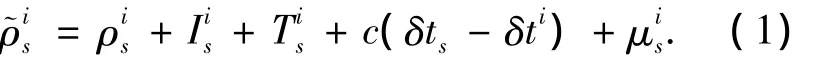
1.2 载波相位观测方程

接收机s对卫星i的载波相位观测方程为

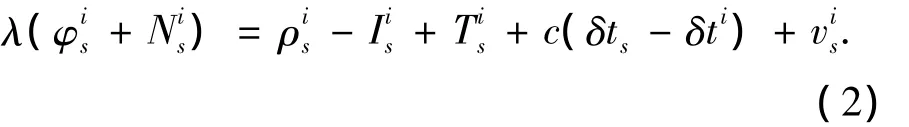
式中:φis为载波相位测量的小数部分;Nis为未知的整周模糊度;λ为L1载波的波长;vis为载波相位测量噪声．

1.3 码单差方程

对于短基线而言，采用单差方法可以消去电离层和对流层误差、卫星轨道误差和卫星时钟误差［4］．若在接收机A和接收机B之间针对同一颗卫星i进行码观测量的单差，则码单差方程为

1.4 载波相位单差方程

码观测量的缺点是噪声较大，因此在高精度测量中主要是利用载波相位观测量，其观测精度相对于码观测量要高2 ～3个数量级［5－6］．对于以A、B两个天线为端点的短基线，其对卫星i的单差载波相位观测方程表述为

根据式(5)，则整理方程为

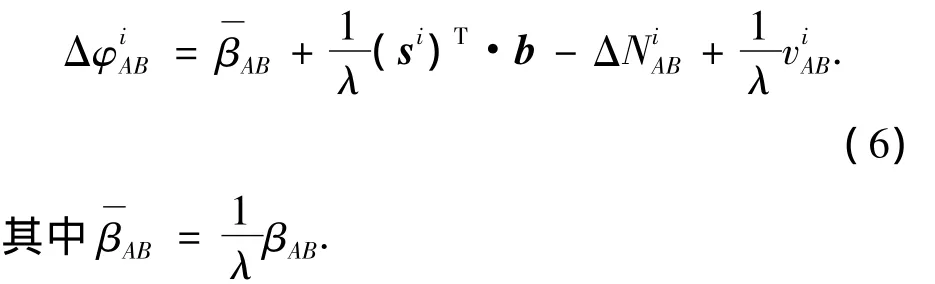
1.5 载波相位双差方程

将2个单差方程相减，可以消去接收机钟差项．假设卫星1仰角最高，作为参考星，则由式(5)可知参考星的单差方程为

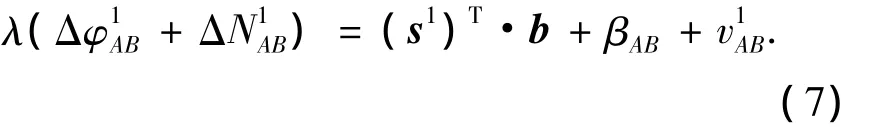
式(5)与式(7)相减可以得到卫星i对参考星的双差载波相位观测方程为

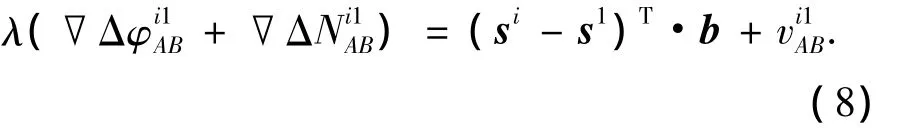
式中:▽ΔφiAB为A、B两个天线到卫星i的双差载波相位观测值的小数部分;▽ΔNiAB为未知的双差整周模糊度．

2 双差观测模型求解载体姿态

2.1 双差观测模型

对于m颗卫星而言，则存在m－1个载波相位双差方程，写成矩阵形式为

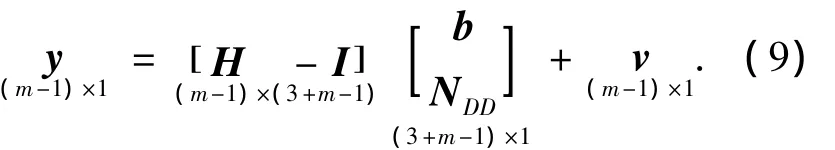
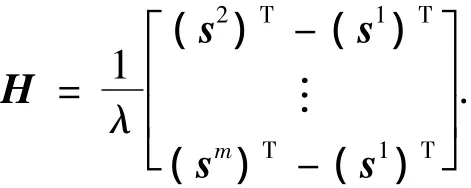
一般认为噪声服从均值为零的正态分布，对于双差载波相位观测值向量y而言，其各个分量存在一定的相关性，y的方差协方差矩阵为

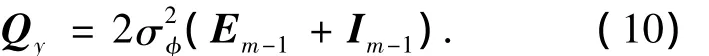
式中:σ2φ为接收机载波相位测量噪声方差，一般认为 σφ=0.025周［7］;Em－1为 m － 1 阶矩阵，其所有元素均为1;Im－1为m－1阶单位矩阵．可见双差观测值y各个分量之间存在强相关性．

式(9)是亏秩的，单历元的情况下无法得到唯一的解，必须将多个历元的观测方程进行联立，通过最小二乘估计未知参数．但最小二乘估计的基线和模糊度参数均为实数解，而模糊度是整数，解决此问题通常是先求解模糊度的浮点解，然后根据其方差协方差矩阵估计模糊度固定解，再利用固定解重新修正基线坐标．

2.2 静态观测模型

对于静态基线，b是保持不变的，对于连续的q个历元有

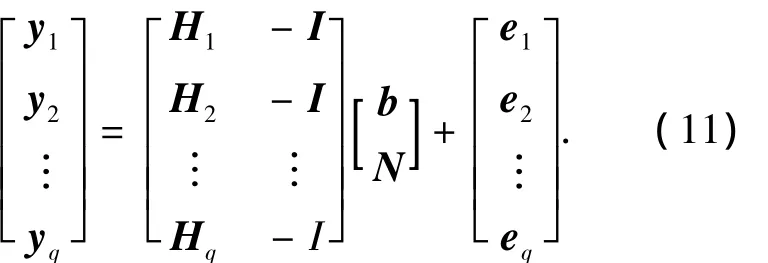
则其数学模型和统计模型可以看成

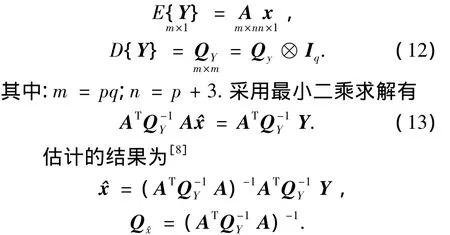
即得到基线向量坐标和模糊度浮点解及其相应的方差协方差矩阵为

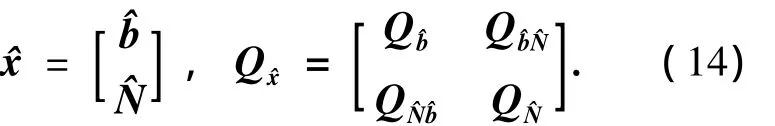
然后通过目标函数最小来求得模糊度固定解为

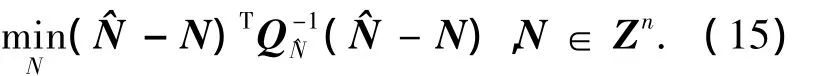
LAMBDA算法是求解式(15)的有效算法．

2.3 动态观测模型

对于动态情况，每个历元k都对应一个不同的基线坐标bk，则其批处理模型为

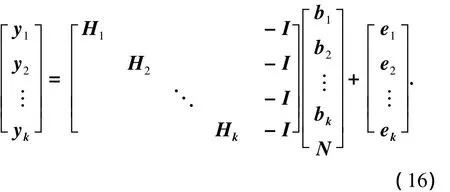
则式(16)中矩阵阶数会随着k的增加而增加，特别是求解各历元的浮点解时，矩阵求逆计算量会非常大，无法满足实时处理的要求．一种解法是将方程组进行解耦变换［9］，即

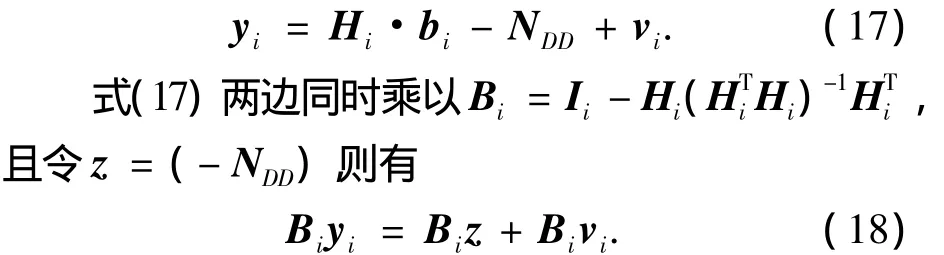
移项有Bi(yi－vi)=Biz，但是观测噪声是未知的，若忽略噪声，可得到模糊度的近似浮点解为

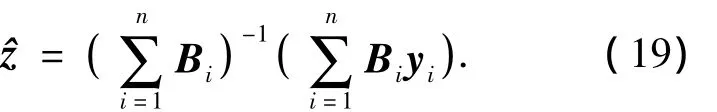
这种做法虽然可以避免大矩阵求逆求得模糊度的浮点解，也易递归实现，但是需要多个历元来等待模糊度浮点解的收敛，即直接收敛法．其收敛的速度曲线基本呈指数衰减的趋势，在开始的2～3 min内，向量NDD可迅速收敛到距真实值2～3个波长λ的位置，以后的收敛速度就变得十分缓慢．要到400～600 s后，NDD才逼近到距真实值NDD＜0.5λ的位置，从而获得正确的NDD．这主要是由于短时间内双差观测量的强相关性造成的，由于式(19)的特殊结构无法准确求得浮点解的方差协方差矩阵，所以无法直接使用LAMBDA算法进行估计．

3 单差观测模型求解姿态模型

3.1 求解单差整周模糊度

假设存在m颗卫星，则根据式(6)和式(4)将分别存在m个载波相位单差方程与m个码单差方程，写成矩阵形式分别为

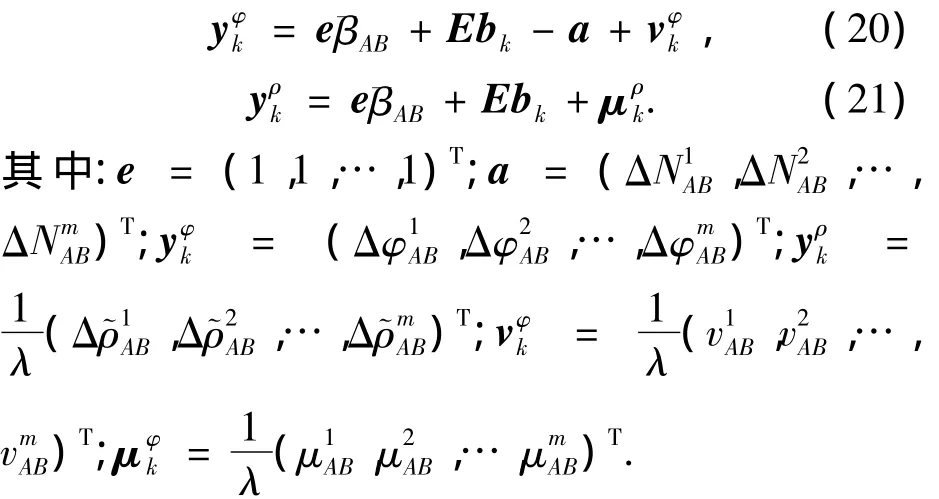
式中E为接收机到卫星的设计矩阵．为了将噪声统计特性归一化［10］，令 σr≡ σφ/σρ，其中:σφ，σρ分别为载波和码噪声的标准差;σr为其比值，一般取为0. 001，将其乘在式(21)的两端，则有

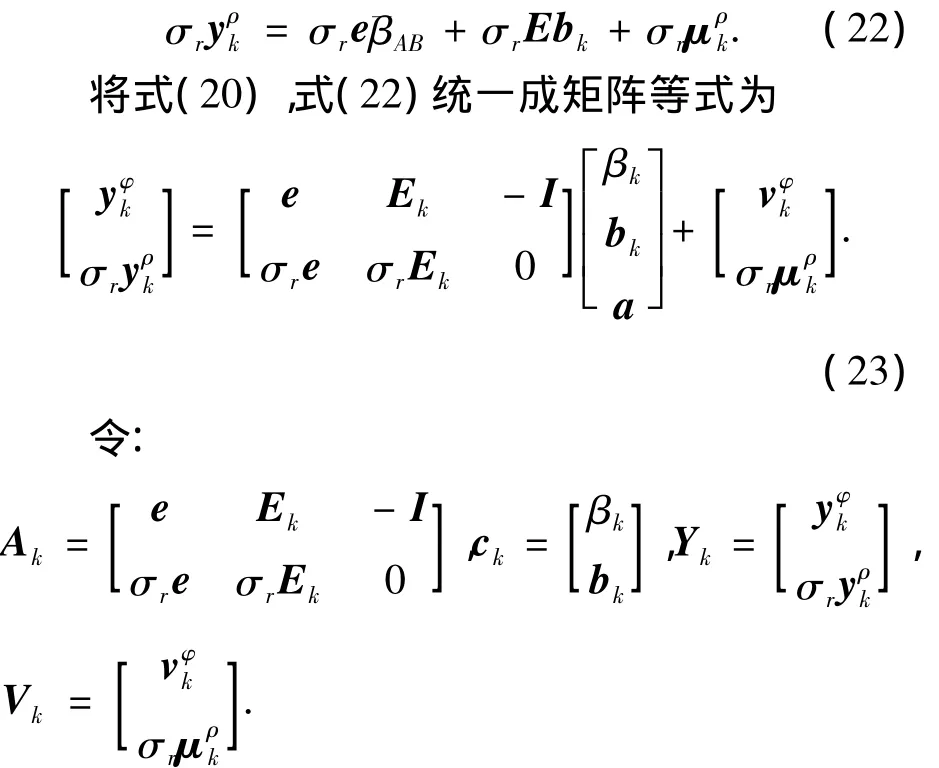
则式(23)等价于

其中a的各个分量均为整数．将k个历元的上述方程进行联立，其矩阵形式为

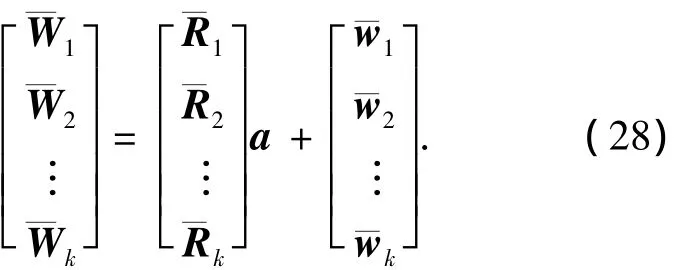
通过Householder变换进行QR分解可以得到正交阵Tk，式(28)两边同时乘以TTk，使得:

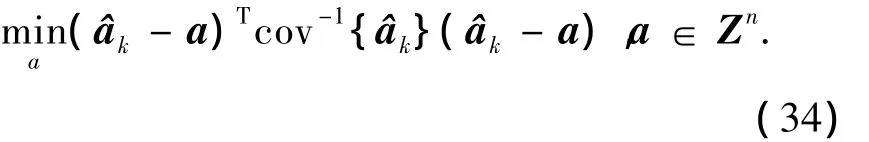
LAMBDA算法对初始模糊度进行Z变换，变换结果为

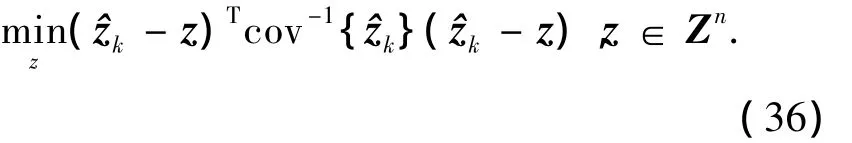
在变换域求解到z，在通过反变换求得原始的双差整周模糊度为

3.2 模糊度检验

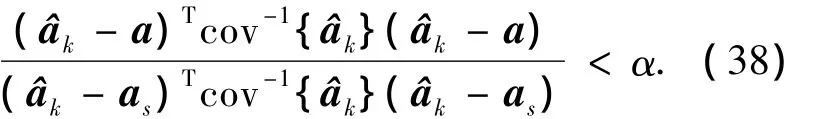
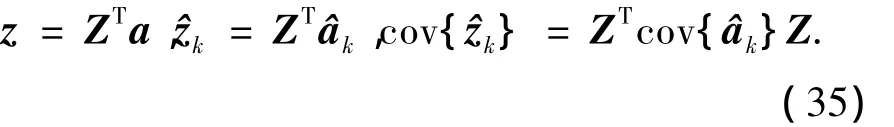
由于各种误差的作用，并不能保证所求出的模糊度就是正确的．因此需要对模糊度候选值进行检验，以得到正确的固定解．工程中最为常用的一种是比率检验，即式中Z矩阵及其转置的作用是对搜索空间进行不同方向的“挤压”，使搜索空间由拉长的高维椭球近似于球，以提高搜索效率，经过变换，式(34)的目标函数等价为

式中:as为次优模糊度固定解;α为常数，其如何选取该关键值仍是一个开放的问题［11］，目前多通过经验选取．为了确保模糊度验证的可靠性，本文采用的方法为如果连续n个历元的基线坐标都通过了基线长度检验且初始整周模糊度的固定解都一致，就可以认为该模糊度求解正确，即看是否满足

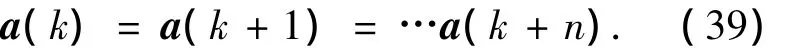
否则，将采用更多个历元继续递归求解，直到可以确定初始整周模糊度．

3.3 求解基线坐标和钟差

求得整周模糊度a，代入式(23)即有

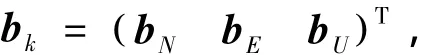
3.4 算法递归实现

在动态载体应用中，数据处理常采用递归的方式，为了便于实现模糊度浮点解的递归估计，利用第k历元估计的结果，则第k+1历元有

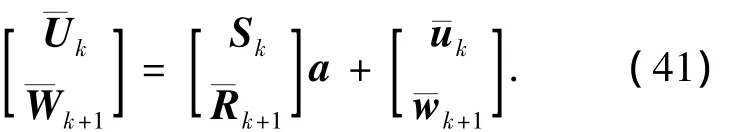
通过 Householder变换实现 QR分解，即式(41)两边同时乘以正交阵TTk+1，即

用k+1个历元的数据得到的初始整周模糊度的浮点估计值为，那么

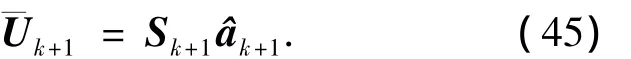
式(45)与式(31)形式统一，即在各历元都可以采用LAMBDA算法对浮点解进行整周模糊度估计．另外，递归算法使用QR分解来完成最小二乘计算，具有数值稳定性，而若使用递归最小二乘法，则会出现随着时间的增长，不可避免的截断误差或舍入误差导致结果偏离真值．

4 附加约束条件下的算法改进

4.1 历元数与模糊度正确性的关系

4.2 扩大候选值空间

减少历元数将导致模糊度浮点解的精度降低，虽然低精度的浮点解经变换后可能落到正确z的邻近整数点的归属域中，但其一定在z的周围．假设其落入z'的归属域，那么以z'为中心一定半径的覆盖范围内的全部归属域所对应的整数点会包含z，如果不包含，则扩大覆盖半径到一定程度，必定包含z．如果能够对通过扩大候选值空间得到的所有候选点进行符合某些准则的判别和检验，从而筛选出正确的整周模糊度，那么则对k的精度也放低．幸运的是，LAMBDA算法能够按照“最佳程度”依次给出多个候选值，这里用“正确候选点出现的位置”表示正确的候选值在多个候选值中的次序．例如若第3个候选值是真实的模糊度，可记作“正确候选点出现的位置为3”．

4.3 根据约束条件筛选候选值

基线长度或俯仰角等约束信息可以辅助筛选正确的整周模糊度，令LAMBDA算法给出的候选值个数为N，具体筛选步骤为:对于某个候选值a'，代入式(40)，求得对应的基线坐标记为b'k，则其基线长度为

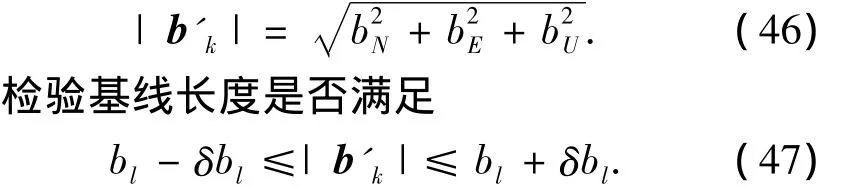
式中:δbl为预先设定的阈值;bl为基线的真实长度．在姿态测量应用中，δbl的选取是基线长度约束的关键．因为天线相位中心的变化和噪声影响，不能将δbl的值设置的过小，同时过大的δbl又无法有效地识别a是否为正确的整周模糊度．该值一般为基线真实长度的1%．

如果由a'得到的b'k满足式(47)，则可利用b'k求解的姿态角继续进行约束检验，即对于地面载体，满足|θ|≤10°;对于有惯性器件辅助的载体，则应满足|θ－|≤δθ并且|ψ－|≤δψ，其中:和分别为惯性器件给出的俯仰角和航向角观测值;δθ和δψ分别为设定的误差变化范围．如果通过该检验，则可认为a'在很大概率上为正确的模糊度．如果连续几个历元计算初始整周模糊度相同，则基本可以确定其为正确解．

如果由a'得到的b'k没有通过基线长度检验或者没有通过姿态角检验，则需要试验下一个模糊度候选值，直到筛选出正确的整周模糊度;如果所有模糊度候选值均不满足，则需扩大候选值个数中的N值，或者需要更多历元继续按照上述方法检测，直至找出满足约束条件的模糊度候选解及其解算得到的姿态角．

5 实际数据测试

为了比较新算法的优势，进行了单基线姿态测量的试验．数据采集地点为北京航空航天大学新主楼楼顶，即尽可能避免信号被遮挡，OEM板型号为NavAtel公司的Super Star II，其载波相位输出频率为1 Hz，天线型号为GPS－701GG，其内含扼流圈，具有多径抑制功能．基线长度为2 m，保持水平放置，持续跟踪的可见星数目为7颗．为了得到初始时刻的双差整周模糊度真值，以作为参考基准，首先采用静态观测模型算法进行求解，通过1 200个历元的观测数据 求 得 NDD= ［ 1， － 9， 7，－ 8，－ 8，7］T，b =［0.868 3，1.805 8，0.017 0］T，ψ =64.320 3°，θ=0.484 9°．

采用动态观测模型的直接收敛法求解，利用式(19)得到的模糊度浮点解的收敛情况如图 1，2所示，其中:“◦”为该时刻浮点解四舍五入后没有映射到正确的整周模糊度上;“·”为映射成功．可以看出直接收敛法确定模糊度分量分别至少需要 452， 465， 543， 335， 478，517 s才会收敛到正确整周模糊度的0.5λ范围内，也即需要近550 s才能保证所有的模糊度分量浮点解四舍五入后收敛到正确的整周模糊度上，进而求解出姿态．

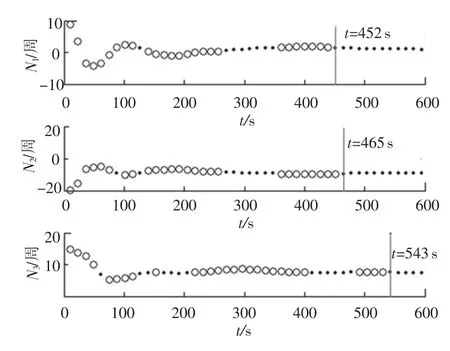
图1 模糊度第 1， 2，3分量收敛情况

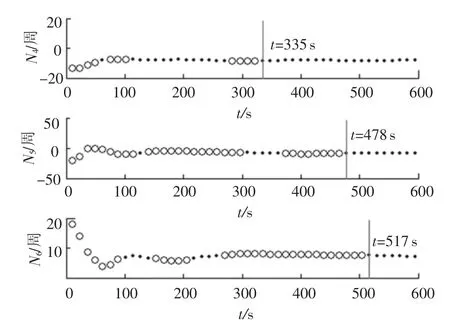
图2 模糊度第 4， 5，6分量收敛情况

采用基于单差模型的算法进行解算，首先假设无基线长度和姿态角约束等先验信息．实验结果如图3所示．结果显示，仅用31 s的观测数据，就可以得到正确的姿态解，解算过程中求得初始时刻的单差整周模糊度为

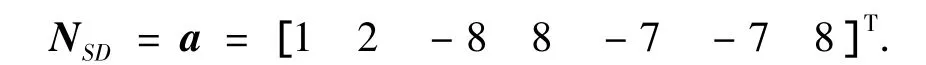
以第1颗星为参考星，可以得到对应的双差整周模糊度N(1)DD，与真实值一致．

图3 姿态角解算结果

对比图3和图4可知，基于单差模型的算法求解姿态的时间要远小于直接收敛法，其原因是单差模型的观测量各个分量之间不相关，同时利用了多个历元的数据递归求得初始时刻整周模糊度的浮点解及其方差协方差矩阵，进而使用LAMBDA算法准确地估计出单差整周模糊度，从而缩短了初始化时间．

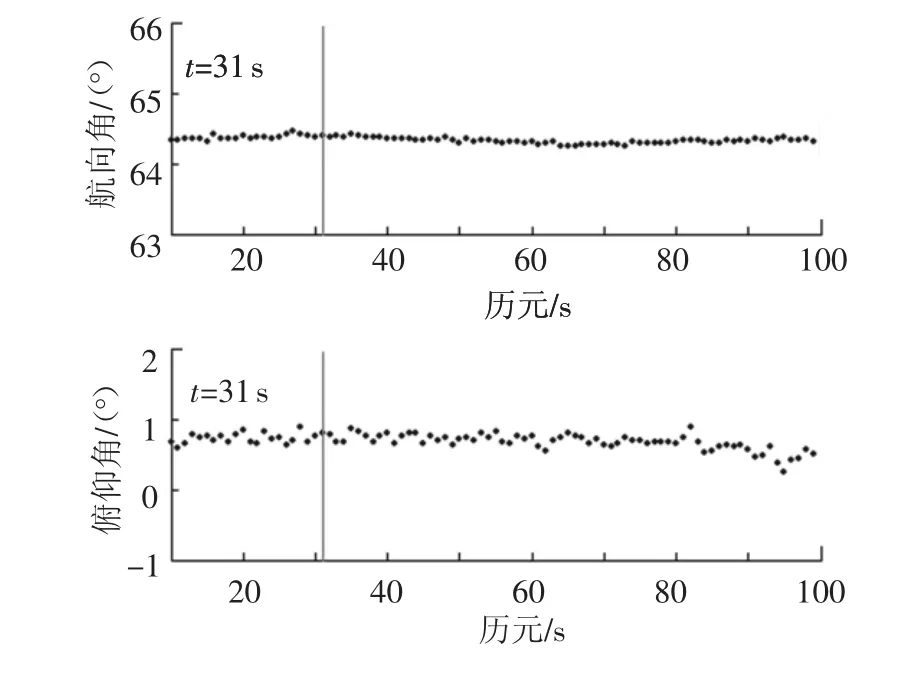
图4 基于约束条件的算法结果

由于基线长度事先可以测量，对于地面载体，俯仰角也存在约束，则可采用附加约束条件下的算法改进的算法求解．为了避免计算量过大，候选值个数N选定为500．实验结果如图4所示，此时初始化时间仅为10 s，小于直接收敛法所用时间的1/50．对比图3可知，比不用约束条件时的初始化时间还要少20 s，从而说明基于约束条件的算法更加有效．图5显示了前100个历元识别到的正确模糊度的位置，在第31 s之前，模糊度正确解是通过约束条件筛选出来的，出现位置虽然较远，但可以看出随着时间的推移其逐渐“向前”靠拢，直至第31 s以后，第1个候选值均为正确解．

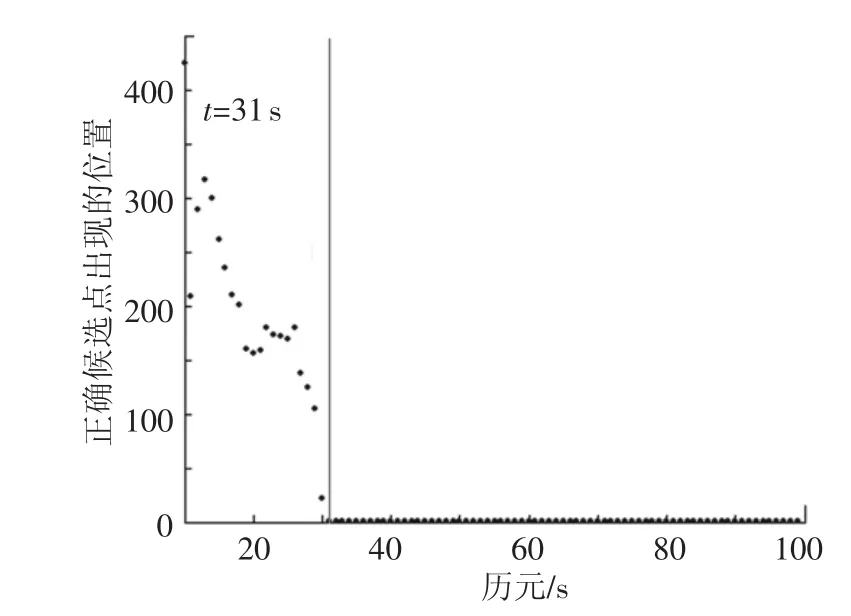
图5 利用基线长度筛选候选点

6 结论

1)采用观测值无关的单差模型，克服了双差模型由于观测值存在相关性而导致的模糊度浮点解收敛速度太慢的缺点．

2)可利用LAMBDA算法提高模糊度估计的准确性．

3)该算法可递归实现，数值计算稳定，计算量较小，能够满足实时应用．

［1］JOHN R．Current issues in the use of the global positioning system aboard satellites［J］．Acta Astronautica， 2000，47(2/9):377－387．

［2］ XIA Kewen，ZHANG Xinying，GAO Jinyong，et al．Study on GPS attitude determination technology based on QPSO algorithm［C］//Proceedings of the 7th World Congress on Intelligent Control and Automation．Washington DC:IEEE，2008:1869－1873．

［3］ CHANG Xiaowen，PAIGE C C，YIN Lan．Code and carrier phase based short baseline GPS positioning:Computational aspects ［J］．GPS Solutions， 2004，7(4):230－240．

［4］HOFMANN-WELLENHOF B．GNSS-Global Navigation Satellite Systems GPS，GLONASS，Galileo，and More［M］．New York:Springer Wien，2008:227－234．

［5］CHANG Xiaowen，PAIGE C C．An orthogonal transformation algorithm for GPS Positioning［J］．SIAM Journal on Scientific Computing， 2002，24(5):1710－1732．

［6］CHANG Xiaowen，PAIGE C C．An algorithm for combined code and carrier phase based GPS positioning［J］．BIT Numerical Mathematics， 2003，43(5):915 －927．

［7］ MISRA P，ENGE P．Global Positioning System:Signals，Measurements，and Performance［M］．2nd ed．Lincoln MA:Ganga-Jamuna Press，2006:238 －239．

［8］VERHAGEN S．The GNSS Integer Ambiguities:Estimation and Validation［D］．Delft:Delft University of Technology，2003:34－35．

［9］俞文伯，高国江，赵剡，等．单频GPS动态相对定位的模糊度逼近搜索解法［J］．北京航空航天大学学报， 2002，28(2):242－244．

［10］CHANG Xiaowen，GUO Ying．Huber＇s M-estimation in relative GPS positioning:Computational aspects［J］．Journal of Geodesy， 2005，79(6):351－362．

［11］VERHAGEN S．Integer ambiguity validation:An open problem［J］．GPS Solution， 2004，8(1):36－43．

An attitude determination algorithm based on GPS single-differenced mode

QIN Hong-lei，CHEN Wan-tong，JIN Tian，CONG Li

(School of Electronic and Information Engineering，Beihang University，100191 Beijing，China，qhlmmm@sina．com)

It is difficult to overcome the high correlation of double differential observation using double-differenced model and the initialization procedure costs a long time with makes it difficult to apply in practice．To deal this problem，a recursive algorithm based on the single-differenced model is presented in which the observations are not correlated．The new method increases observation information with the aid of code for original carrier phase observation．At the same time the float ambiguity solutions and its variance-covariance matrix can be obtained recursively and it makes the LAMBDA method be used to estimate the integer ambiguities．The method is also less computation with numerical stability．The experiment results show that the time of initialization is reduced to about 1/50 of that using the double-differenced method，so this method can be effectively applied in practical attitude determination for shortening initialization procedure．

GPS;attitude determination;integer ambiguity;short baseline

V249.3

A

0367－6234(2011)09－0105－07

2010－01－08．

国家高技术研究发展计划资助项目(2009AA12Z313)．

秦红磊(1975—)，男，博士，副教授．

(编辑 张 红)