升力式再入飞行器再入轨迹优化分析

黄育秋，何麟书

（北京航空航天大学宇航学院，100191 北京，huanyuqiu@163.com）

升力式再入飞行器再入轨迹优化分析

黄育秋，何麟书

（北京航空航天大学宇航学院，100191 北京，huanyuqiu@163.com）

在充分调研分析国内外轨迹优化方法的基础上，选择直接法将升力式再入飞行器的再入轨迹优化问题转化成参数优化问题，而后采用序列二次规划法来解该参数优化问题，并采用C++语言编写了优化算法，最后进行了再入飞行器的最大射程轨迹优化分析.仿真结果表明，采用本文所述的方法能够对升力式再入飞行器这一类轨迹优化问题进行优化分析，并具有较好的优化效果.

再入飞行器;轨迹优化;直接法;序列二次规划

传统的弹道式再入飞行器和弹道－升力式再入飞行器存在两大缺点，即存在造成再入器及其有效载荷损伤的着陆冲击过载和由于各种干扰造成的不易控制的大落点散布［1］.升力式再入飞行器的出现有效的克服了这两种缺点，是航天技术取得的巨大进步.升力式再入飞行器和传统的再入飞行器相比，升力式再入飞行器升力的增大和可调整，大大增加了飞行器机动飞行的能力.平缓的再入段和大范围的机动飞行能力，使升力式再入飞行器水平着陆到指定机场跑道和实现全球快速打击成为可能，正因为如此，升力式再入飞行器具有重要的经济和军事意义.二战后，美国就开始了升力式再入飞行器的研究，比较富有代表性的计 划 包 括:BOMI、Dyna － Soar、Alpha Draco、BGRV、HGV、CAV/HTVs、X －37 等.1940 年末到1950年初，苏联进行了Silbervogel飞行器的风洞试验，并积累丰富的试验数据.1960年中期，Mikyan设计局设计了自己的升力式再入飞行器Mig－105.最近，俄罗斯已秘密研制了新型再入机动飞行的白杨－M导弹［2］.

由于升力式再入飞行器的飞行速度较快，飞行空域较大，飞行环境复杂，而且其可能的飞行轨迹多为跳跃滑翔轨迹，在轨迹设计中需要考虑控制、动压、过载、气动热等限制，成为总体设计中的一个难点，而轨迹优化理论正是解决该问题的有效途径.

自上世纪中后期，升力式再入飞行器再入轨迹优化问题便逐渐被提出，并成为诸多学者研究的焦点，相继出现了多种轨迹优化方法，归纳为解析解法和数值解法两大类.解析解法是运用Pontryagin极大值原理，在不考虑过程约束的情况下给出一些飞行的最优解析解.随着研究的深入和飞行任务的需要，人们慢慢地把研究的焦点转向了数值解法［3］.数值解法是指利用离散的参数来逼近整个系统，使轨迹优化问题转化为参数优化问题，然后采用合适的算法解参数优化问题.数值解法主要包括轨迹优化问题的转化和解参数优化问题两部分.

就轨迹优化问题的转化方法来讲，数值解法主要有直接法和间接法两类.直接法是将连续的轨迹优化问题直接离散进行参数化，无需求最优解的必要条件.间接法是利用Pontryagin极大值原理推导出最优控制的一阶必要条件，从而得到求解最优轨迹的Hamiltonian边值问题(HBVP).相比直接法，采用间接法求解最优轨迹问题存在理论推导复杂、求解困难等缺陷［4－5］.

结合以上分析，本文采用数值解法对升力式再入飞行器的最大射程弹道进行优化分析，选择直接法将该轨迹优化问题转化成参数优化问题，而后采用序列二次规划法来解该参数优化问题，并采用C++语言编写了优化算法，进行了仿真分析，最后给出了相应的仿真结果.

1 飞行器轨迹优化理论

本文采用直接法将该轨迹优化问题转化成参数优化问题，而后采用序列二次规划法来解该参数优化问题，下面将阐述其相关理论.

1.1 轨迹优化问题的一般描述

轨迹优化问题一般可以描述为:确定容许控制u(t)∈Rm和参量p∈Rnp，使得由1个微分方程组确定的系统，从给定的初始状态过渡到终端状态，并使性能指标函数J达到最小，同时满足规定的约束.其数学描述如下［6－8］:

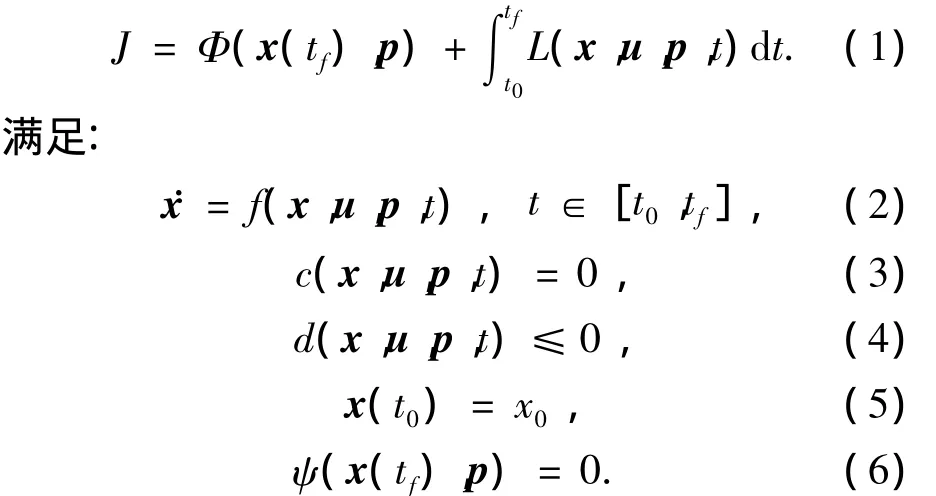
其中，x(t)∈Rn，表示系统的状态变量;t表示时间变量.标量性能指标函数J，由末值型性能指标函数Φ(x(tf)，p)和积分型性能指标函数组成，其被积函数为 L(x，u，p，t)，并且积分是从 t0时刻到tf时刻.式(2)表示系统状态方程，式(3)表示状态变量、控制变量和参量的等式约束，式(4)表示状态变量、控制变量和参量的不等式约束，式(5)表示状态变量的初始条件，式(6)表示状态变量和参量的终端条件.

1.2 参数化过程

1)划分时间区间［t0，tf］为N个子区间，节点为 ti，即 t0＜ t1＜ … ＜ tN－1＜ tN=tf.

2)控制变量的参数化.在每个子区间t∈［ti，ti+1］，(i=0，1，…，N － 1)，将控制变量近似为

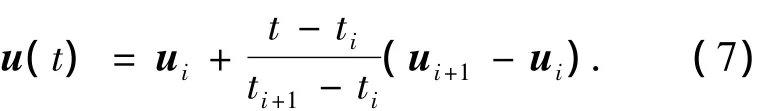
3)价值函数、约束函数的参数化.假设给定了1个猜测的控制输入量和参量，即，在初始条件方程(5)下，从t0时刻到tf时刻积分状态方程组(2)，得到的状态变量随时间的变化历程可以表示为x(，t)，也就是说，利用控制输入量和参量可以唯一地确定状态量，进而得到价值函数J以及约束c、d、ψ，据此约束可以离散成1个等式约束向量g∈Rnc(N+1)+nf和不等式约束向量h∈

用上述的参数化策略，有限维的最优控制问题，(即方程组(1)～(6))被近似化为有限维的非线性规划问题［9－10］:

1.3 序列二次规划法

方程(8)所表示的非线性规划问题可以采用如下序列二次规划方法求解:

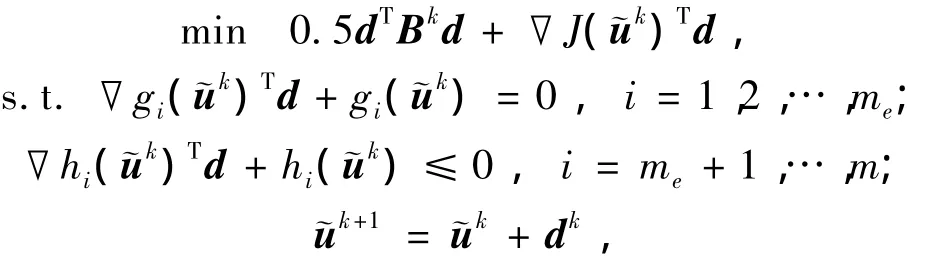
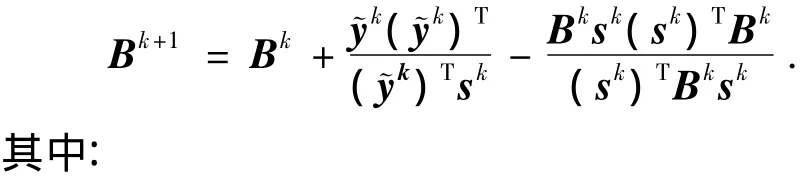
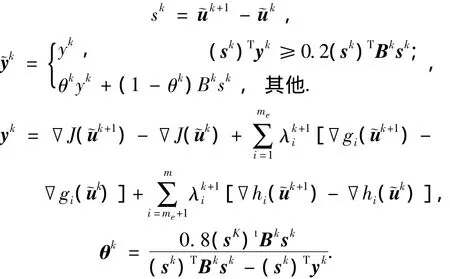
矩阵Bk的初值B0一般取为单位阵，即B0=I［11－13］.其算法流图如图 1 所示.

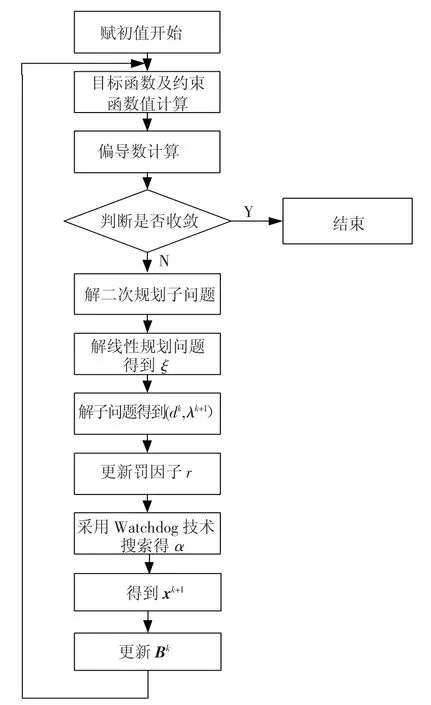
图1 算法流程

2 再入飞行器最大射程弹道优化模型

2.1 再入飞行器的动力学模型

考虑地球自转和地球扁率的情况下，再入飞行器的动力学模型为［1］

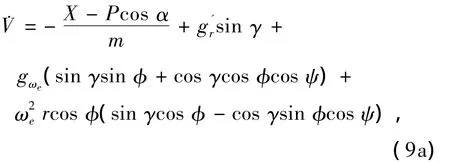
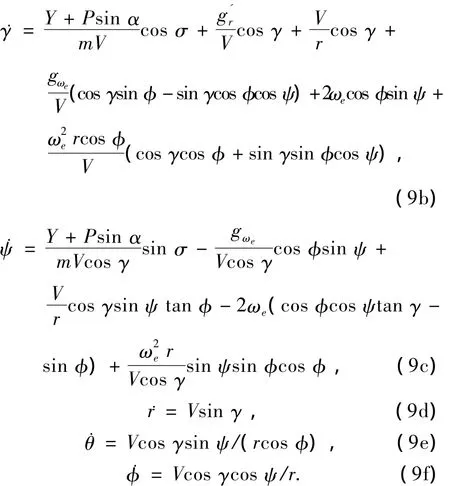
射程Lr由再入点的经纬度和飞行器当前点的经纬度通过球面三角形可以求得.

2.2 再入飞行器最大射程弹道优化模型

1)性能指标J.最大射程的性能指标为

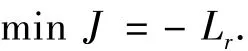
2)优化控制量u(t).由再入飞行器的控制方式可以得到优化控制量为

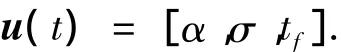
3)约束条件.攻角α约束为5°≤α≤15°;倾侧角σ约束为|σ|≤70°;攻角变化率约束为||≤10(°/s);倾侧角变化率约束为||≤20(°/s);滑翔段最大高度 hmaxh约束为 hmaxh≤65 km;动压q约束为q=0.5ρV2≤40 kPa;法向过载ny约束为|ny|=|N/mg0|≤2，其中N为体系下的法向力;末端高度约束为30 km≤hf≤40 km;末端速度约束为Vf=2 000 m/s;气动加热率约束为

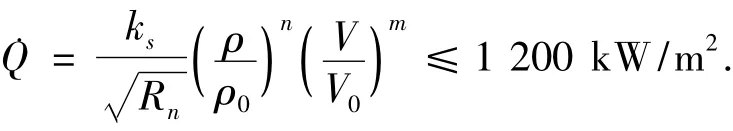
其中:Rn为鼻锥驻点区曲率半径;V0为第一宇宙速度;ρ0为海平面标准大气密度;ks、m、n为常数，可取理论计算值或实验值，本文取ks=17 600，n=0.5，m=3.15，Rn=0.04 m.

3 仿真分析

基于前文的研究基础，采用推力为零时的方程(12)以及2.2节中的轨迹优化模型，应用直接法和序列二次规划法对升力式再入飞行器的最大射程弹道进行优化分析，其相应的仿真结果如图2～10所示.

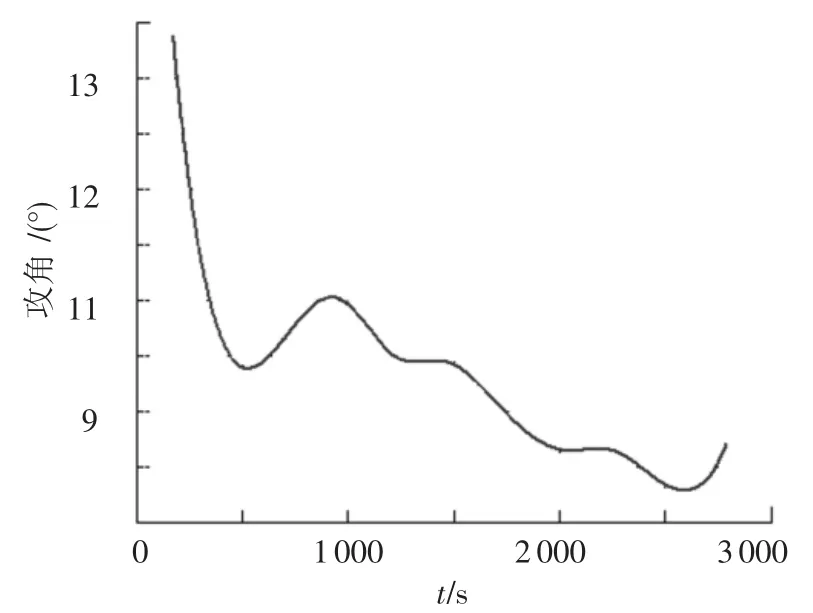
图2 攻角曲线

图3 倾侧角曲线

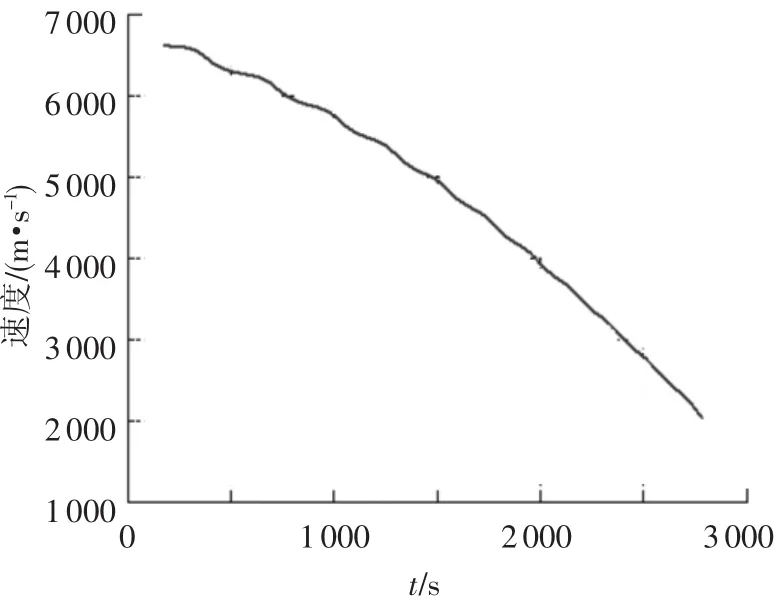
图4 速度曲线

最大射程是典型的弹道优化性能指标，可以反映出再入飞行器的滑翔能力以及优化算法的优劣，通过图2～11可得:

1)图2、3显示了升力式再入飞行器2个主要的控制变量在其滑翔飞行时的变化规律，可以看出再入初期飞行器以最大攻角减速以满足气动加热率的要求，而后飞行器以最大升阻比攻角飞行，倾侧角则一直保持在0°左右，直到后期需要机动时才有较大变化，且控制量均在给定的变化范围之内;

2)从图4、5可以看出，飞行器的速度是稳定减小的，最大滑翔高度为65 km，且跳跃的幅度比较稳定，这说明根据优化所得的控制量可以稳定控制飞行器的再入飞行;

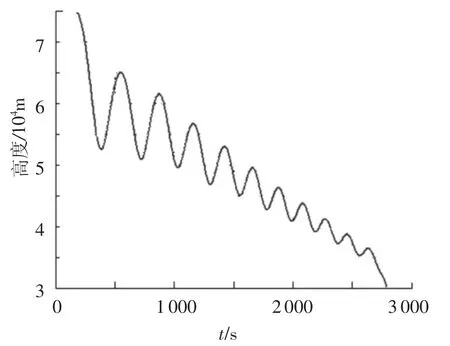
图5 高度曲线

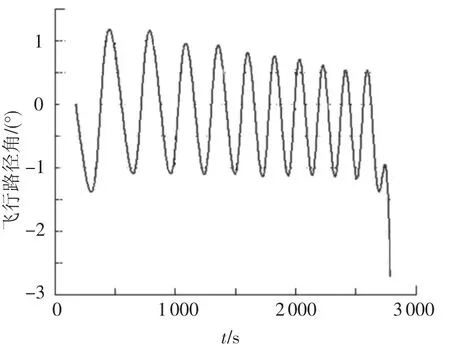
图6 飞行路径角曲线

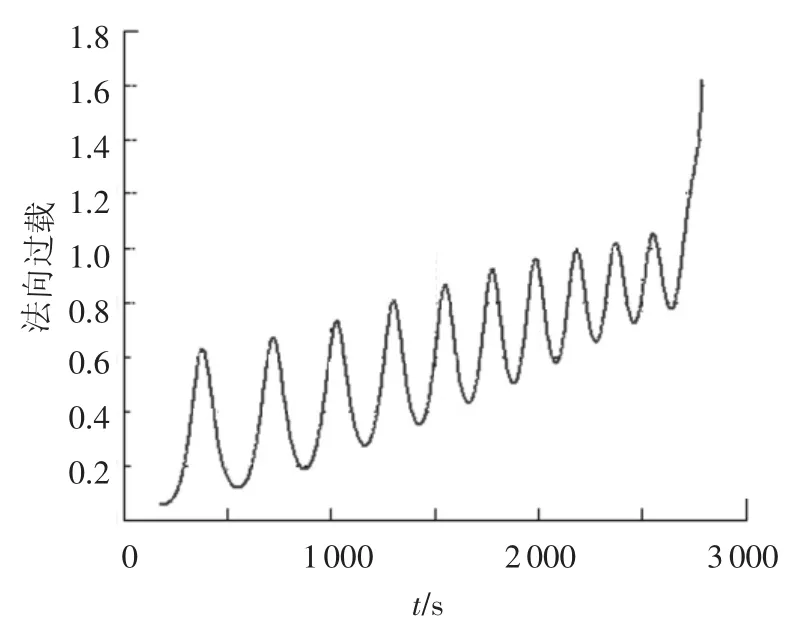
图7 法向过载曲线

3)图6～9反映了再入飞行器滑翔飞行时的部分特征参量的变化，其中最大法向过载为1.6、最大动压为 37 kPa、最大气动加热率为1 190 kw/m2，均满足给出的约束条件;

4)图10表明飞行器在满足所有约束的情况下，滑翔 2 616.11 s，期间获得的最大射程为12 670.0 km，满足一般设计中对升力式飞行器射程的要求.

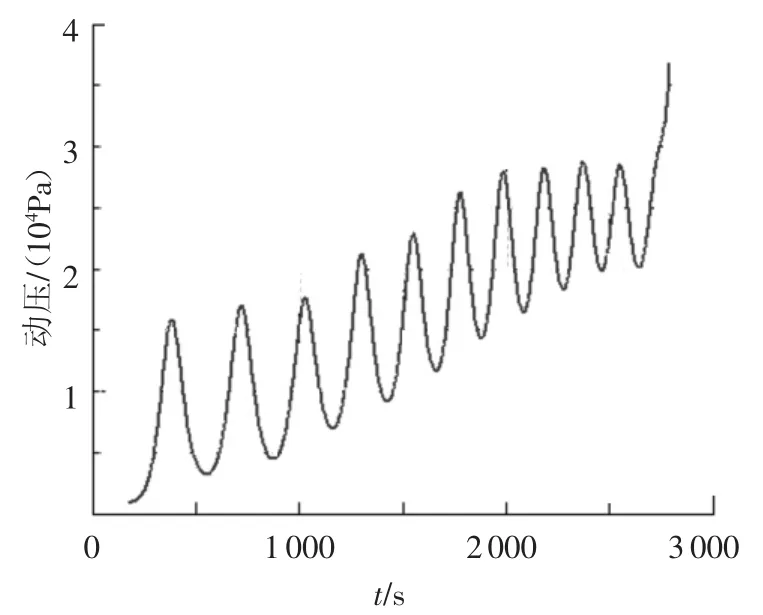
图8 动压曲线

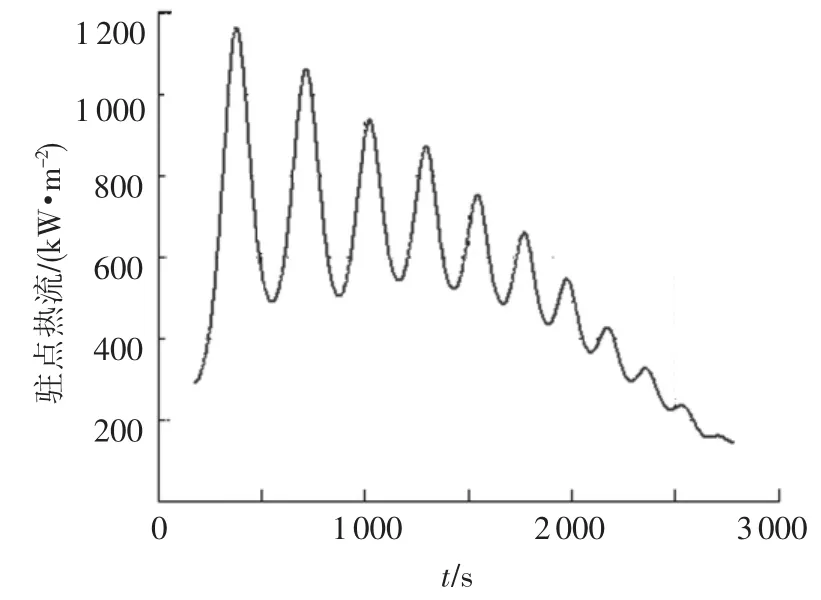
图9 气动加热率曲线

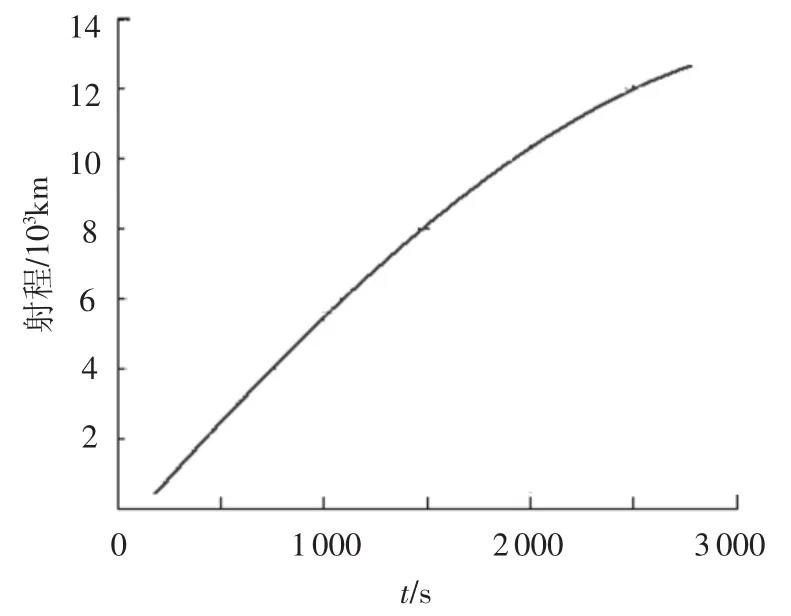
图10 射程曲线

综上，采用本文所述的直接法和序列二次规划方法能够对升力式再入飞行器这一类轨迹优化问题进行优化分析，并具有较好的优化效果.

4 结 论

升力式再入飞行器飞行速度快、飞行环境复杂、并受到多种约束条件的限制，轨迹优化方法能够很好的解决其轨迹设计问题.本文首先给出了轨迹优化问题的一般描述，基于直接法的参数化方法，序列二次规划算法，从而设计了一套基于直接法和序列二次规划方法的轨迹优化算法;其次建立了再入飞行器的动力学模型和轨迹优化模型;最后在前文的研究基础上完成了仿真分析，论证了本文提出的轨迹优化算法对于再入飞行器轨迹优化的适用性.后续的研究将涉及再入飞行器其他特征轨迹的优化问题，以及飞向固定目标的轨迹优化问题.

［1］赵汉元.飞行器再入动力学和制导［M］.长沙:国防科技大学出版社，1997:382－384.

［2］李瑜，杨志红，崔乃刚.助推－滑翔导弹弹道优化研究［J］.宇航学报，2008，29(1):67 －69.

［3］LEWALLEN J M，TAPLEY B D，WILLIAMS S D.Iteration proceduresforindirecttrajectory optimization methods［J］.Journal of Spacecraft and Rockets，1968，5(3):321－327.

［4］JACKSON M C，STRAUBE T M，FILL T J，et al.Onboard determination of vehicle glide capability for the shuttle abort flight manager(SAFM)［C］//IEEE Aerospace and Electronic Systems Society，Core Technologies for Space Systems Conference.Colorado Springs:［s.n.］，2002.

［5］BRAIN C F.Some tools for the direct solution of optimal control problems［J］.Advances in Engineering Software，1998，29(1):45 －61.

［6］VINH N X，CHERN J S，LIN C F.Phugoid Oscillations in Optimal Reentry Trajectories［J］.Acta Astronautica，1981，8:311－324.

［7］PANTOJA J F O De O，MAYNE D Q.A sequential quadratic programming algorithm for discrete optimal controlproblemswith controlinequality constraints［C］//Proceedings of the 28thIEEE conference on decision and control.Piscataway:IEEE，1989.

［8］PETER F G.CAMTOS-A software suite combining direct and indirect trajectory optimization methods［D］.Stuttgart:University of Stuttgart，2002:10 －28.

［9］BARRON R L，CHICK C M.Improved indirect method for air-vehicle trajectory optimization［J］.Journal of Guidance，Control，and Dynamics，2006，29(3):643 －652.

［10］BETTS J T.Survey of numerical methods for trajectory optimization ［J］.Journal of Guidance，Control，and Dynamics.1998，21(2):193－207.

［11］SHIPPEY B M.Trajectory optimization using collocation and evolutionary programming for constrained nonlinear dynamical systems［D］.Arlington:University of Texas，2008.

［12］VINH N X，LU P.Chebyshev minimax problems for skip trajectories［J］.Journal of the Astronautical Sciences，1988，36(1):179－197

［13］YONG E，TANG G J，CHEN L.Three-dimensional Optimal Trajectory for Global Range of CAV［C］//Proceedings of the 1st International Symposium on Systems and Control in Aerospace and Astronautics.Harbin:［s.n.］，2006:1396－1400.

Entry trajectory optimization of lift reentry vehicle

HUANG Yu-qiu，HE Lin-shu

(Dept.of Astronautics，Beijing University of Aeronautics and Astronautics，100191 Beijing，China，huanyuqiu@163.com)

In this paper，on the basis of review of trajectory optimization method at home and abroad，the direct method and sequential quadratic programming algorithm is used to solve the trajectory optimization problem.The trajectory optimization problem is transformed into a parameter optimization problem using direct method and the parameter optimization problem is solved using sequential quadratic programming.A trajectory optimization algorithm is written using C++，and a numerical simulation of maximum range entry trajectory is performed.The simulation results show that the technology of trajectory optimization for lift reentry vehicle proposed in this paper is reasonable and feasible with good results.

reentry vehicle;trajectory optimization;direct method;sequential quadratic programming

V412

A

0367－6234(2011)09－0139－05

2010－06－18.

黄育秋(1968—)，女，博士研究生;

何麟书(1938—)，男，教授，博士生导师.

(编辑 张 宏)