三次样条齿线圆柱齿轮齿面接触分析

苏进展，方宗德，蔡香伟

(西北工业大学 机电学院，710072西安，sujinzhan@mail．nwpu．edu．cn)

三次样条齿线圆柱齿轮齿面接触分析

苏进展，方宗德，蔡香伟

(西北工业大学 机电学院，710072西安，sujinzhan@mail．nwpu．edu．cn)

对三次样条齿线圆柱齿轮滚切加工和齿面几何接触进行了分析．在推导修形滚刀齿面方程的基础上，利用三次样条齿线滚切原理和啮合方程得到其齿面数学模型;根据两齿面在啮合中连续相切条件，建立了考虑安装误差的齿面接触分析(TCA)模型．齿面接触分析仿真结果表明，用抛物线形齿廓刀具对齿面修形，可获得抛物线型的几何传动误差，改善了啮合性能;在安装误差条件下，调整控制结点位置可降低接触印痕对安装误差的敏感性．

三次样条齿线圆柱齿轮;滚切加工;齿面接触分析;齿面修形

圆柱齿轮广泛应用于机械传动系统中．目前，许多研究工作都集中在齿廓，而对齿线的研究还比较少，主要有直线、螺旋线、抛物线［1］等．近些年来，国内外研究学者对圆弧齿线进行了研究，证明了圆弧齿线圆柱齿轮具有综合强度高和承载能力大的特点，在实际工程中得到了一定的应用［1－7］．圆弧齿线圆柱齿轮的啮合性能对安装误差较为敏感，通过增大刀盘半径可以降低误差敏感性［3］，但却减小了齿轮副的重合度，从而影响传动的平稳性［6］．Litvin 等［8－9］研究了各种修形方式的圆柱齿轮，以降低对安装误差敏感性和振动噪声．

本文在圆弧齿线圆柱齿轮的基础上，提出了三次样条齿线圆柱齿轮，研究了滚切加工方法，对齿面啮合进行仿真．比较分析两种不同齿线的齿轮副，结果表明，三次样条齿线圆柱齿轮可降低接触印痕对安装误差的敏感性，提高齿轮副的承载能力．该圆柱齿轮设计和加工方法对研究其他圆柱齿轮的各种齿形、齿线及综合拓扑修形都具有参考价值．

1 三次样条齿线展成原理

三次样条齿线是在圆弧齿线的基础上提出的，如图1所示．M1、M2为圆弧齿线上点，M'1、M'2为三次样条齿线上控制结点;以点 N1、M'1、G、M'2、N2为结点，圆弧齿线端点 N1、N2处切矢(最大螺旋角)作为三次样条齿线端点的切矢条件，构造出如下三次样条函数:

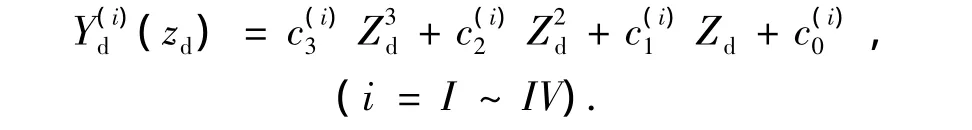
所得三次样条齿线是二阶导数连续的光滑曲线，与圆弧齿线具有相同单一凹凸性，否则需要重新确定控制结点位置;调整M'1、M'2得到不同齿线，保证在N1、N2处螺旋角不变．本文齿线设计方法:通过调整控制结点位置，使得齿线在齿宽中点附近区域螺旋角的变化较小，达到降低接触印痕对安装误差的敏感性的目的．

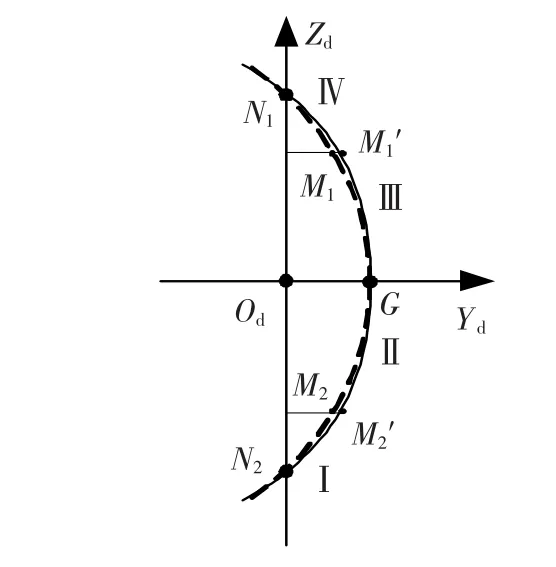
图1 三次样条齿线

图2为六轴联动NC(Numerical Control)滚齿机示意图，滚刀安装角转动A，滚刀转动B，工件转动C;滚刀沿着工件径向运动X、切向运动Y、轴向进给运动Z．如图3所示，由三次样条齿线上任一点的切矢和法矢相互垂直，可以得到滚刀位置lz(lz=Zd)与滚刀安装角φe(φe=φA+β，φA为滚刀轴线与Yd夹角，β为滚刀导程角)之间的关系式为

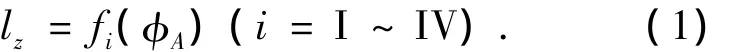
对式(1)求导可得到滚刀沿着Zd的速度为

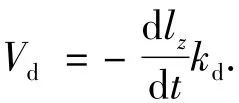
工件安装角和工件转角的关系式为

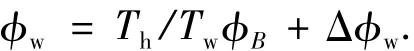
其中，φw、φB、Δφw分别为工件转角、滚刀转角、附加转角(即将滚刀沿着切向方向位移ly=Y(i)d(lz)转化到工件转角，Δφw=ly/rw，rw为齿轮节圆半径);Th、Tw为滚刀头数、齿轮齿数．滚刀需要轴向运动和径向运动而没有切向运动，工件与滚刀的角速度之间关系式为

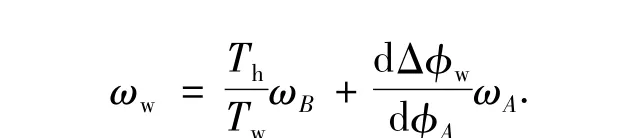
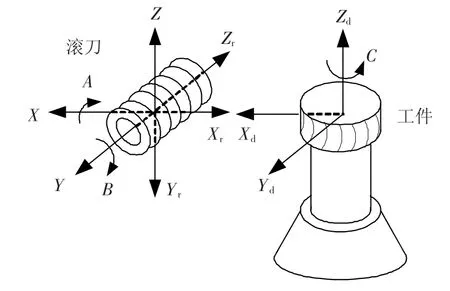
图2 六轴联动NC滚齿机示意图

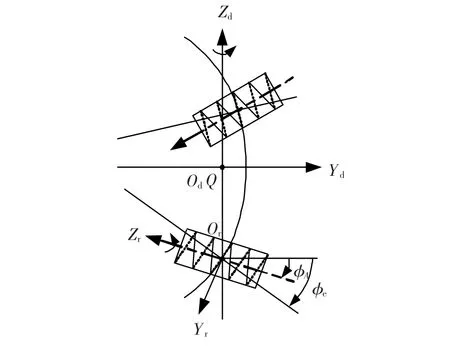
图3 三次样条齿线展成原理

2 滚刀齿面方程

本文采用法截面为直线型齿廓的右旋ZN型蜗杆滚刀加工三次样条齿线圆柱齿轮，其齿面方程推导可参考文献［ 1， 3，10 －11］．坐标系 Sc固联在滚刀的法截面上，αn为滚刀压力角，β为滚刀导程角，bn为节圆处齿宽，采用抛物线齿廓代替直线齿廓对滚刀法截面齿廓进行修形．从图4可以得到刀具齿廓位置矢量为

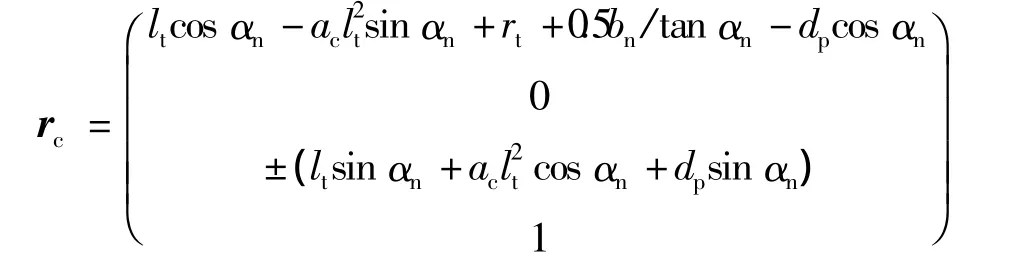
图5为滚刀齿面展成坐标系，Sb和Sh分别为滚刀参考坐标系和滚刀齿面动坐标系，滚刀齿面位置矢量和法向矢量为

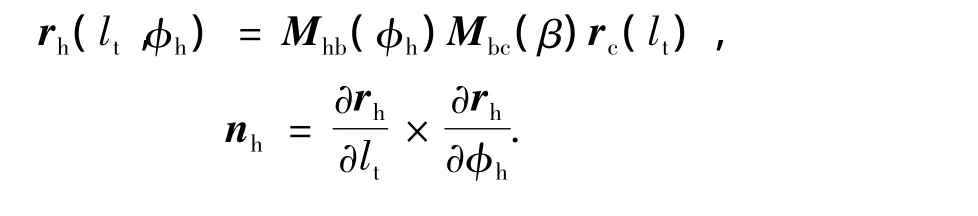
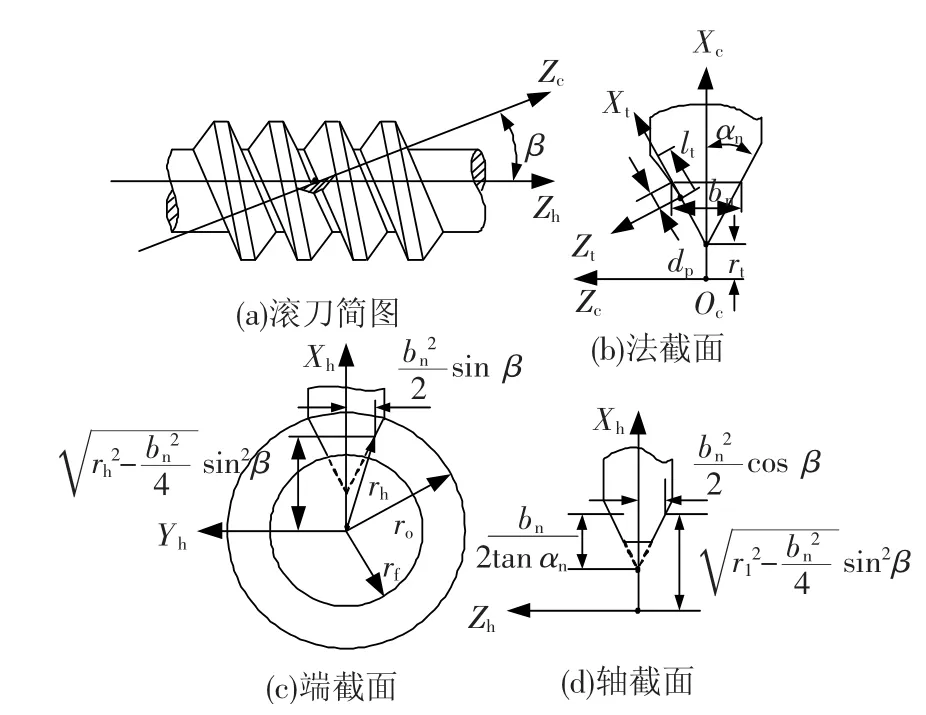
图4 蜗杆滚刀

图5 滚刀齿面展成坐标系

其中，Mbc为Sc到Sb的齐次变换矩阵，Mhb为Sb到Sh的齐次变换矩阵．

3 啮合方程

图6为六轴联动NC滚齿机的加工坐标系．

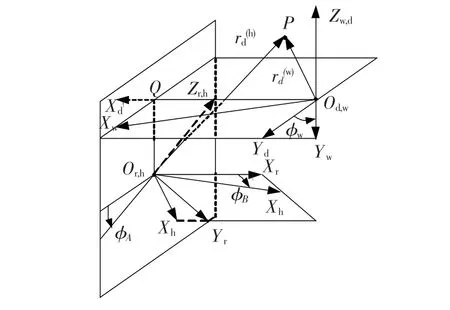
图6 滚切加工坐标系

坐标系 Sh、Sr、Sw、Sd分别为滚刀动坐标系、滚刀固定坐标系、齿轮动坐标系、齿轮固定坐标系;φB、φw分别为滚刀加工转角、齿轮转角．滚刀安装φA在加工过程中按照式(1)规律变化，同时沿着Zr轴向进给运动Vd和沿着Xr的径向进给运动，以保证滚切出完整齿形．齿面的位置矢量和法向矢量为

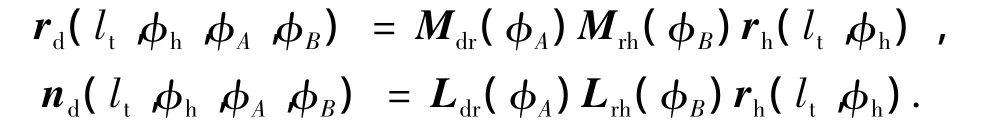
式中，Mrh为Sh到Sr的齐次变换矩阵，Mdr为Sr到Sd的齐次变换矩阵，Lrh、Ldr分别为 Mrh、Mdr的旋转变换矩阵．

切削过程中，满足以下的啮合方程:

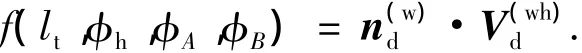
其中，相对速度为V(wh)d=V(w)d－V(h)d．齿轮切削点P的速度为V(w)d=ww×r(w)d，ww=wwkd为齿轮转动的角速度，r(w)d为P点的位置矢量;滚刀对应的P点的速度为

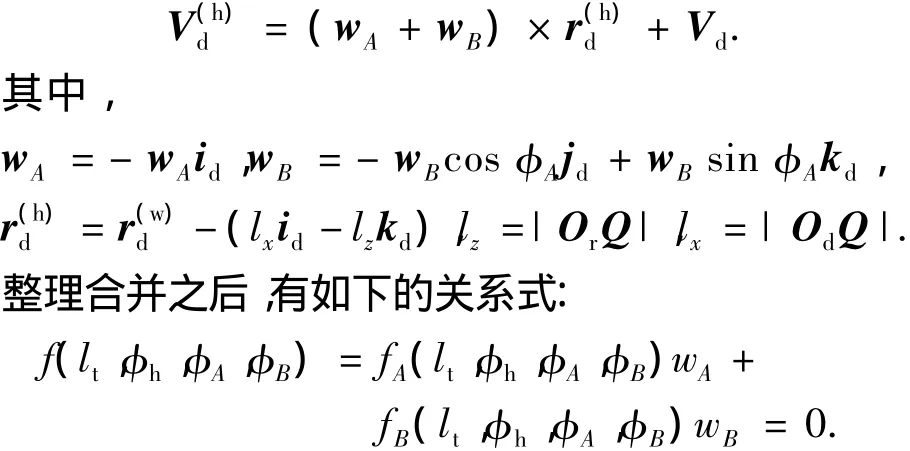
由于加工中转角φA、φB均为独立变量，有如下的两个啮合方程:

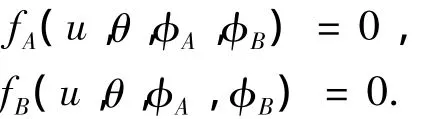
在齿轮动坐标系Sw下，齿面的位置矢量和法向矢量为

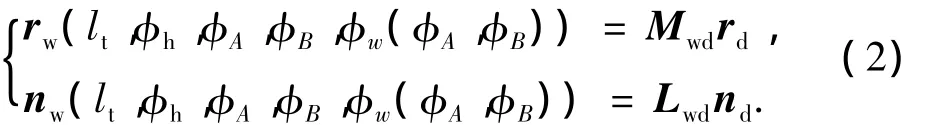
式中:Mwd为Sd到Sw的齐次变换矩阵，Lwd为Mwd的旋转矩阵．

4 齿面接触分析

齿轮副啮合坐标系(图7)中，坐标系S1、Sn分别为小轮的动坐标系、固定参考坐标系;S2、Sm分别为大轮的动坐标系、固定参考坐标系;Sk和Sv是模拟安装误差的辅助坐标系，其中Δγv为垂直安装误差，Δγk为水平安装误差，ΔC为中心距安装误差，C为齿轮副中心距，φ1、φ2分别为小轮和大轮的啮合转角．小轮和大轮齿面的位置矢量r1、r2和法向矢量n1、n2可分别用式(2)求得，并在固定坐标系Sn中表示为

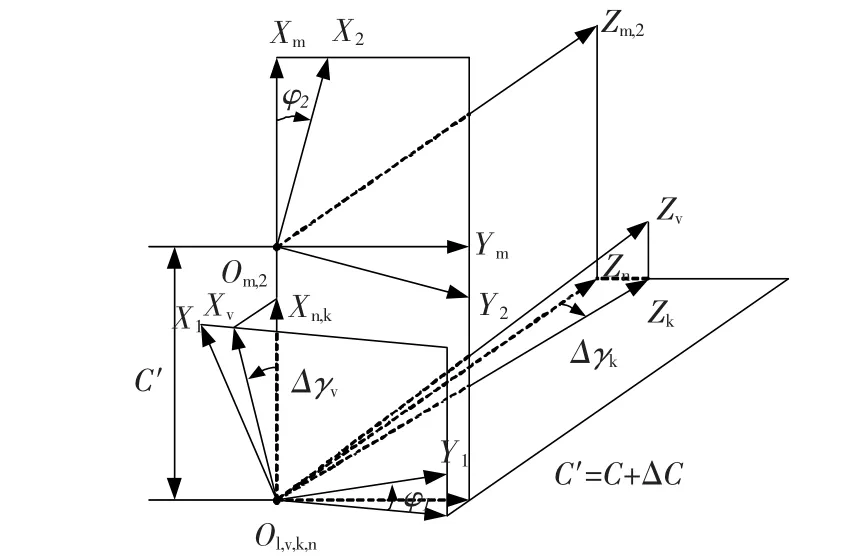
图7 齿轮啮合坐标系

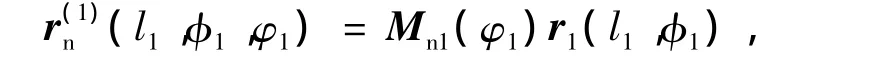
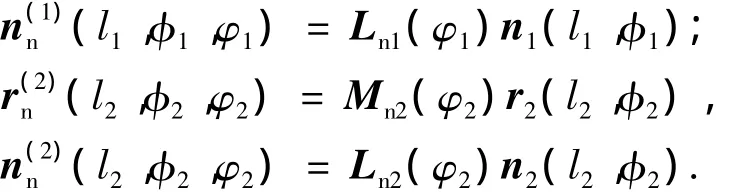
式中，Mni=MnkMkvMvi(i= 1，2)分别为Si到Sn的齐次变换矩阵，Lni为Mni的旋转变换矩阵．根据小轮和大轮齿面Σ1、Σ2在小轮固定坐标系Sn中连续相切接触条件，得到以下TCA基本方程组:

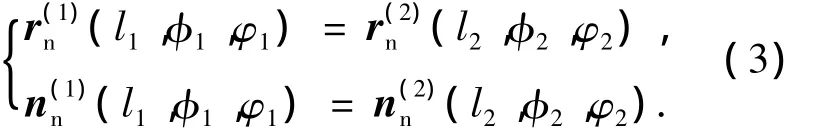
其中，l1、φ1为小轮的齿面参数，l2、φ2为大轮的齿面参数．式(3)包含6个标量方程，但由于|nn(1)|=|nn

(2)|= 1，所以只有5个独立的标量方程，而未知量却有6个，取φ1为输入量，求式(3)可得到两齿面的一个接触点，再以固定步长改变小轮的啮合转角φ1值，继续求解，直至所求出的接触点超出两齿面的有效边界，从而获得接触迹线．定义传动误差定义为

式中:φ02、φ01为大小轮初始啮合转角，Z2、Z1为大轮齿数、小轮齿数．

5 算例

蜗杆滚刀和齿轮副设计参数如表1所示，表2、表3是两次调整控制结点位置所得的三次样条齿线系数，第一次调整时控制结点M'1=( 15，6.4)和M'2=(－ 15，6.4)，第二次调整时控制结点M'1=( 15，6.8)和M'2=(－ 15，6.8)．以小轮凹面和大轮凸面为研究对象，分别对修形前后齿轮副进行TCA分析，得到齿面接触印痕和传动误差见图8;图9为2种齿轮副在同等安装误差条件下3种设计方案的接触印痕．

表1 蜗杆滚刀和齿轮副设计参数

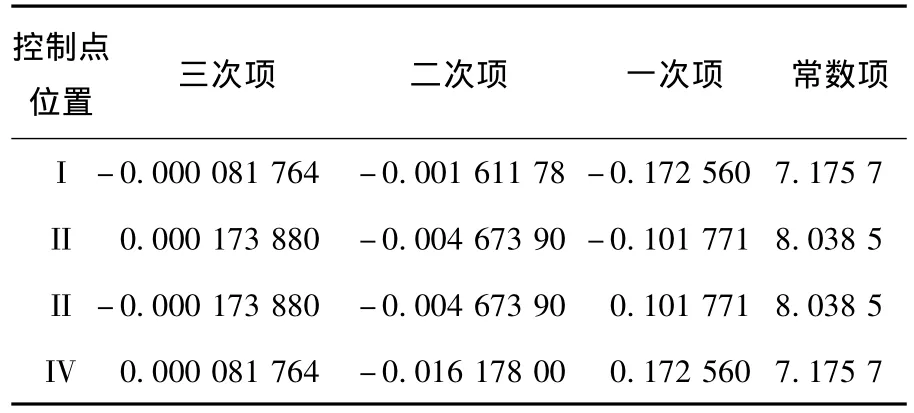
表2 三次样条齿线系数(第一次调整)

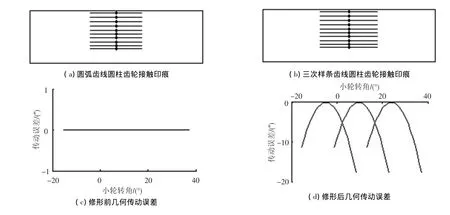
图8 不考虑安装误差接触印痕和传动误差

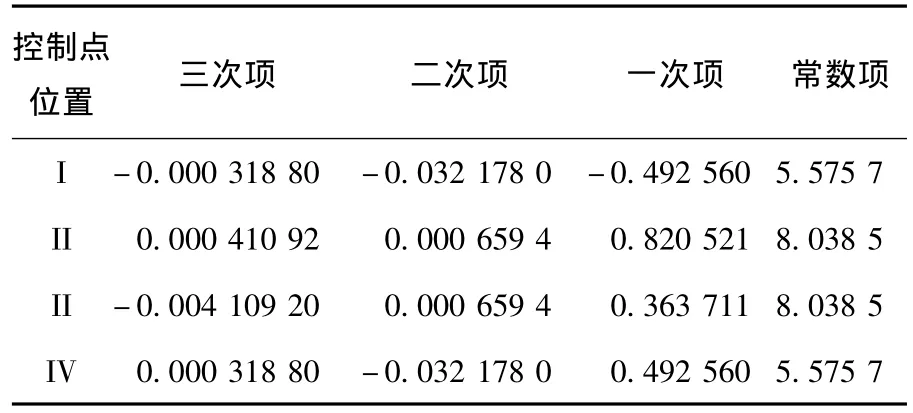
表3 三次样条齿线系数(第二次调整)

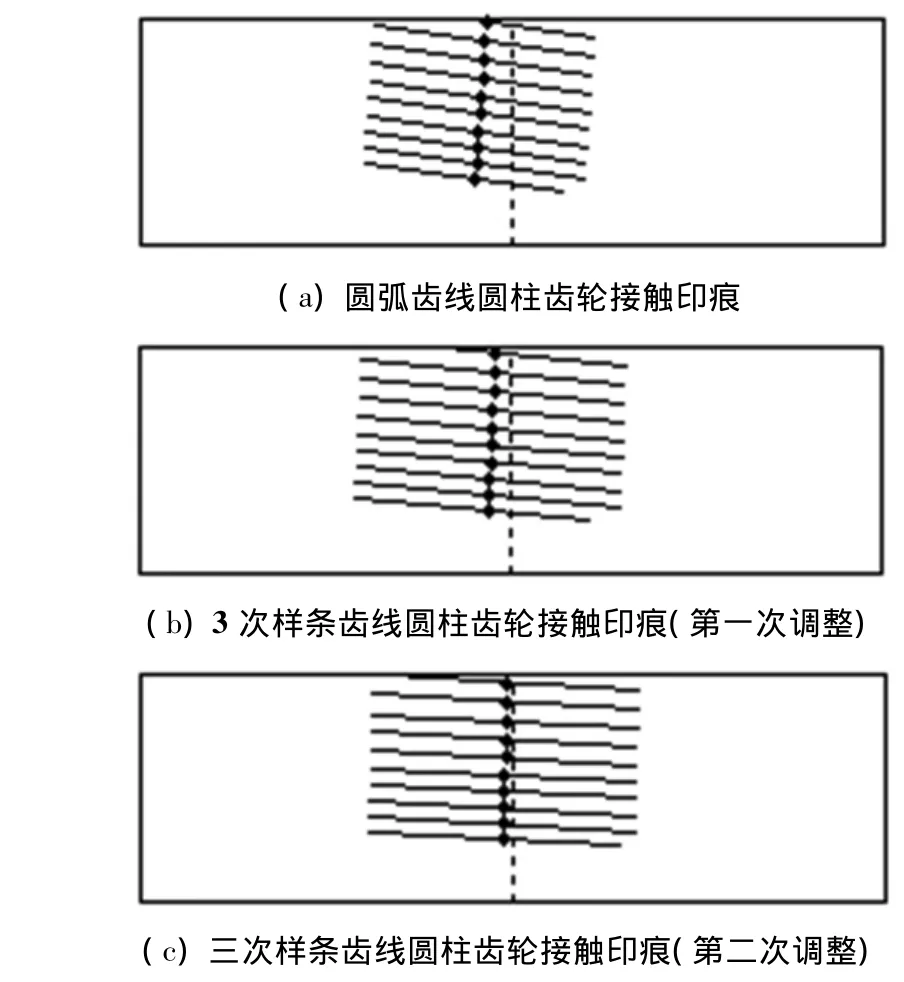
图9 三种齿轮副接触印痕

从图8可以看出，对于未经过修形的齿轮副，其传动误差为零，经抛物线齿廓修形后，产生的抛物线型传动误差曲线可吸收由安装误差产生线性误差［8］．传动误差幅值可由齿廓抛物线系数ac来确定，ac增大，传动误差幅值随之增大，图8(b)为第一次调整时接触印痕，同时也可以看出三次样条齿线圆柱齿轮接触椭圆长轴较圆弧线要长．图9为考虑安装误差条件为 Δγv=－ 0.12°，Δγk=0.1°，ΔC=0.05 mm的接触印痕变化;在不同误差误差组合下，接触印痕将偏离齿宽中心，至于偏向左端或者右端是由安装误差向量来确定的，可由TCA程序计算得到;由多种组合安装误差条件下齿轮副TCA仿真结果可以看出，三次样条齿线圆柱齿轮副接触印痕对安装误差敏感性较圆弧线圆柱齿轮副低(在同等安装误差条件偏离齿宽中心的程度小);图9(a)为圆弧齿线圆柱齿轮副偏离齿宽中心情况，可以看出其接触印痕偏离程度比三次样条齿线圆柱齿轮副(图9(b)、(c))大．从图9(b)、(c)也可以看出:第二次调整后齿轮副的接触印痕偏离程度较第一次的偏离程度低;通过调整控制结点得到的三次样条齿线圆柱齿轮可降低对安装误差的敏感性;因此，所设计的三次样条齿线圆柱齿轮副可产生抛物线形几何传动误差和接触印痕对安装误差敏感性低的特性，可以提高齿轮副的啮合性能．

6 结论

1)在圆弧齿线圆柱齿轮的基础上设计了三次样条齿线圆柱齿轮，通过刀具对齿面进行抛物线修形，获得抛物线形几何传动误差．修形后的齿轮副可避免边缘接触及吸收由安装误差引起的不连续几何传动误差，传动误差的幅值可由抛物线齿廓参数控制．

2)采用TCA方法，比较分析了两种齿轮副接触印痕对安装误差的敏感性，结果表明，三次样条齿线齿轮副可有效降低对接触印痕对安装误差敏感性．

3)可以通过不断调整三次样条控制结点位置来改变齿线形状，达到优化啮合性能的目的．

［1］牛艳萍，苏进展．抛物线齿线圆柱齿轮啮合特性研究［J］．机械设计， 2010，27(6):27－30．

［2］WU Y C，CHEN K Y，TSAY C B．Contact characteristics of circular-arc curvilinear tooth gear drives［J］．Journal of Mechanical Design， 2009，131(9):081003－1:8．

［3］TSENG R T，TSAY C B．Undercutting and contact characteristics of cylindrical gears with curvilinear shaped teeth generated by hobbing［J］．Journal of Mechanical Design， 2006，128(5):634－643．

［4］TSENG R T，TSAY C B．Contact characteristics of cylindrical gears with curvilinear shaped teeth［J］．Mechanism and Machine Theory， 2004，39(4):905－919．

［5］马振群，王小椿，沈冰．对称弧线齿线圆柱齿轮的真实齿面接触分析研究［J］．西安交通大学学报， 2005，39(7):722－725．

［6］马振群．对称弧线圆柱齿轮的设计制造机关键技术研究［D］．西安:西安交通大学，2005．

［7］戴玉堂，有贺幸则，姜德生．圆弧齿线圆柱齿轮的数控滚切机理与试验研究［J］．中国机械工程， 2006，17(6):706－709．

［8］LTIVIN F L，FUENTES A，GONZALEZ-PZEREZ I，et al．Modified involute helical gears:computerized design，simulation of meshing and stress analysis［J］．Comput Methods Appl Mech Engrg，2003(192):3619－3655．

［9］LITVIN F L，FAN Q，VECCHIATO D，et al．Computerized generation and simulation of meshing of modified spur and helical gears manufactured by shaving［J］．Comput Methods Appl Mech Engrg，2001(190):5037－5055．

［10］吴序堂．齿轮啮合原理［M］．北京:机械工业出版社，1982．

［11］LITVIN F L，FUENTS A．Gear geometry and applied theory［M］．Cambridge:Cambridge University Press，2004．

Contact characteristics of cylindrical gear with cubic spline tooth traces

SU Jin-zhan，FANG Zong-de，CAI Xiang-wei

(School of Mechanical Engineering，Northwestern Polytechnical University，710072 Xi’an，China)

Contact characteristics and hobbing cutting of cylindrical gear with cubic spline tooth traces are investigated．On the basis of the derivation of the hobbing cutter’s tooth surface，the hobbing generated method and gearing theory，the mathematical model of cylindrical gear with cubic spline tooth trace was developed．And，the tooth contact analysis model in which the assemble errors was also considerated，was established on the conditions of continuous tangency of two contact surfaces．The computerized simulation of meshing and contact shows that the meshing characteristics of the modified gears can be improved by using the generating tool with parabolic curved profile which obtains a parabolic transmission error curve;the sensitivity of contact pattern of the cylindrical gear with cubic spline tooth traces can be reduced by adjusting the position of control nodes．

cylindrical gear with cubic spline tooth traces;hobbing cutting;tooth contact analysis;tooth modification

TH132

A

0367－6234(2011)09－0112－05

2010－05－26．

国家自然科学基金资助项目(50875211)．

苏进展(1982—)，男，博士后;

方宗德(1948—)，男，教授，博士生导师．

(编辑 杨 波)