Newmark积分方法在负刚度时的数值稳定性分析

李 爽，翟长海，刘洪波 ，3，谢礼立 ，2

(1.哈尔滨工业大学 土木工程学院，150090 哈尔滨，shuangli@hit.edu.cn;2.中国地震局工程力学研究所，150080 哈尔滨;3.黑龙江大学建筑工程学院，150080 哈尔滨)

Newmark积分方法在负刚度时的数值稳定性分析

李 爽1，翟长海1，刘洪波1，3，谢礼立1，2

(1.哈尔滨工业大学 土木工程学院，150090 哈尔滨，shuangli@hit.edu.cn;2.中国地震局工程力学研究所，150080 哈尔滨;3.黑龙江大学建筑工程学院，150080 哈尔滨)

为了获得Newmark积分方法在负刚度时的适用性，研究了Newmark积分方法在负刚度时的数值稳定性分析方法并对其稳定性进行了分析，分析了Newmark积分方法中的参数、阻尼和分析步长对积分方法稳定性的影响规律.结果表明其稳定性与正刚度时差异较大，在负刚度时不再具有无条件稳定性.对于正刚度时常用的Newmark积分参数α=1/4、δ=1/ 2，在负刚度时仅当分析步长大于某一值时积分方法才能保证稳定性，因此难以同时满足稳定性和准确性的要求.推荐了通过选取合适的Newmark积分参数获得稳定性的方法.为Newmark积分方法用于分析具有负刚度的结构时的适用性提供了依据，也为积分方法的合理选择提供了参考.

Newmark积分方法;负刚度;稳定性;阻尼;分析步长

在动力反应分析过程中，结构刚度可能出现负定的情况.产生这一现象的原因可源于一些材料在加载至荷载极限点后变形增加荷载反而减少，进而引起结构荷载－位移曲线出现负刚度段;也可源于几何非线性效应，附加的几何刚度引起结构荷载－位移反应出现负刚度段.在时域逐步积分方法中，Newmark积分方法是求解结构动力反应的常用方法.关于Newmak积分方法在正刚度时的数值稳定性问题已有大量研究［1－6］，一致的结论是该积分方法在积分参数α≥(0.5+δ)2/4且δ≥1/2时是无条件稳定的.Newmark积分方法的无条件稳定性是在结构具有正刚度时获得的，负刚度时是否成立需进一步研究.然而，目前对于结构刚度矩阵为负定时积分方法稳定性的探讨仅限于少量研究.文献［7］指出Newmark常平均加速度方法 ( α=1/4、δ=1/2)满足屈服后负刚度条件下数值积分的稳定性要求.文献［8］虽没有直接研究负刚度情况方法的稳定性，但指出在负刚度情况下Newmark方法中参数取值为α=1/4、δ=1/2时精度较低，而取 α=1/12、δ=1/2时得到的结果较好.文献［9］通过研究得到的结果为负刚度情况下取α≥(0.5+δ)2/4且δ≥1/2时是条件稳定的.从目前的研究水平来看，关于负刚度情况Newmak方法稳定性方面的研究并不全面，而且也没有形成一致的认识和结论.

本文研究了Newmark积分方法在负刚度时的数值稳定性分析方法并对其稳定性进行了分析.同时，详细分析了Newmark积分方法中的参数、阻尼和分析步长等对积分方法稳定性的影响规律.

1 负刚度时稳定性分析方法

结构的荷载－位移曲线可以采用线性化的方法处理为分段线性形式，最不利的情况下也可以假定在每一计算时间步长内或迭代步长内结构为一线性体系.因此，对于方法稳定性分析可转化为给定刚度情况下积分方法的稳定性分析.使用单自由度线性体系讨论积分方法的稳定性，动力平衡方程为

式中:t+Δt¨u、t+Δt˙u和t+Δtu分别为t+Δt时刻结构加速度、速度和位移;t+Δt¨ug为t+Δt时刻的地震动加速度;ξ为阻尼比;ω为自振频率;r为体系的刚度系数，弹性阶段r= 1，屈服后r=k1/k0，负刚度时r＜0.k0为初始刚度，k1为第二刚度.

可以将式(1)表示为以下递推形式

矩阵A和向量L分别为积分逼近算子和荷载算子.

对于使用Newmark积分方法求解式(1)的情况，当式(1)中r=1时A矩阵的标准形式已有研究给出［1］．当 r≠1 时，可将式(1)写成如下形式

通过特征多项式|A－λI|= 0，得到A的3个特征值分别为

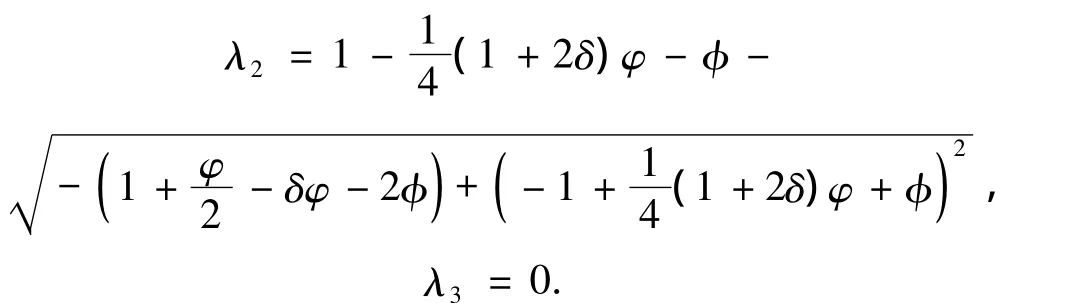
积分逼近算子A是3×3型矩阵，且有3个互不相同的特征值，根据矩阵理论，其所对应的初等因子必皆为一次.稳定性的判别根据文献［10］中给出的负刚度时方法稳定性的判断准则进行判断，满足下式即认为方法稳定

2 负刚度时Newmark积分方法的稳定性分析

2.1 Newmark方法中参数的影响

在正刚度情况下，一般选用分析步长Δt/T=1/10～1/ 20，T为结构周期，所以本文也给出在此种情况下负刚度时的情况.图1给出了Newmark参数 δ=1/2、阻尼比 ξ=0.05 时 ρ(A)/eμΔt值随Newmark参数α和负刚度系数r的变化规律.当Δt/T=1/10时，存在一个峰值带，在此区域内的ρ(A)/eμΔt值远大于 1，即处于此区域内 Newmark积分方法不稳定;在其他区域内，ρ(A)/eμΔt值接近1或小于 1，图1(a)和(c)中非网格区域 ＜1.当刚度系数r接近于0时，α的变化对ρ(A)/eμΔt值的变化影响较小.随着刚度系数r的减小，α的变化对ρ(A)/eμΔt值变化的影响为先增大然后部分区域会出现峰值带，而后减小;当刚度系数r较小时，较小或较大的α值对应的方法均是稳定的，而中等大小的α值对应的方法却是不稳定的.当Δt/T=1/20时，没有出现像Δt/T=1/10时所出现的峰值带，随刚度系数r减小或随α的增大ρ(A)/eμΔt值呈增大趋势. 对 Δt/T=1/10 和Δt/T=1/20的两种情况，α取小值时均是稳定的，并且此时刚度系数r的影响很小.

图2为Newmark参数α=1/4、阻尼比ξ=0.05时ρ(A)/eμΔt值随 Newmark参数 δ和刚度系数 r的变化规律.当Δt/T=1/10时且刚度系数r接近于0时，δ的变化对ρ(A)/eμΔt值的变化影响较小;ρ(A)/eμΔt值有随刚度系数r减小而增大的趋势，随δ的增大而增大的趋势.图2(a)和(c)中非网格区域＜ 1，因此仅当r较小时才能保证方法的稳定性.Δt/T=1/20时，无论刚度系数r和δ取何值均能保证方法的稳定.ρ(A)/eμΔt值在刚度系数r接近0时接近 1，有随刚度系数r减小而减小的趋势，有随δ增大而增大的趋势.

2.2 阻尼的影响

图3为Newmark参数α =1/4、δ=1/2时ρ(A)/eμΔt值随阻尼比 ξ变化的情况.可以看出如果分析时间步取小一点，阻尼的影响也相应的小.但是，对于 α=1/4、δ=1/2的情况，ρ(A)/eμΔt均是 ＞ 1 的，无论阻尼比取何值方法均是不稳定的.

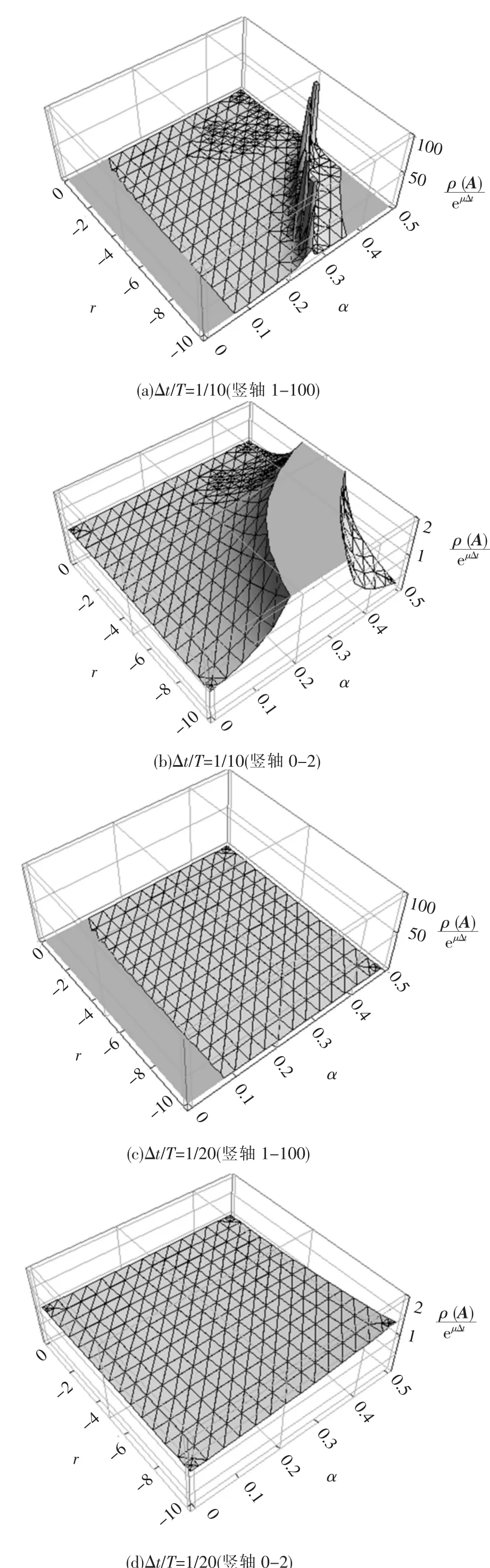
图 1 δ=1/2、ξ=0.05 时 ρ(A)/eμΔt随 α的变化

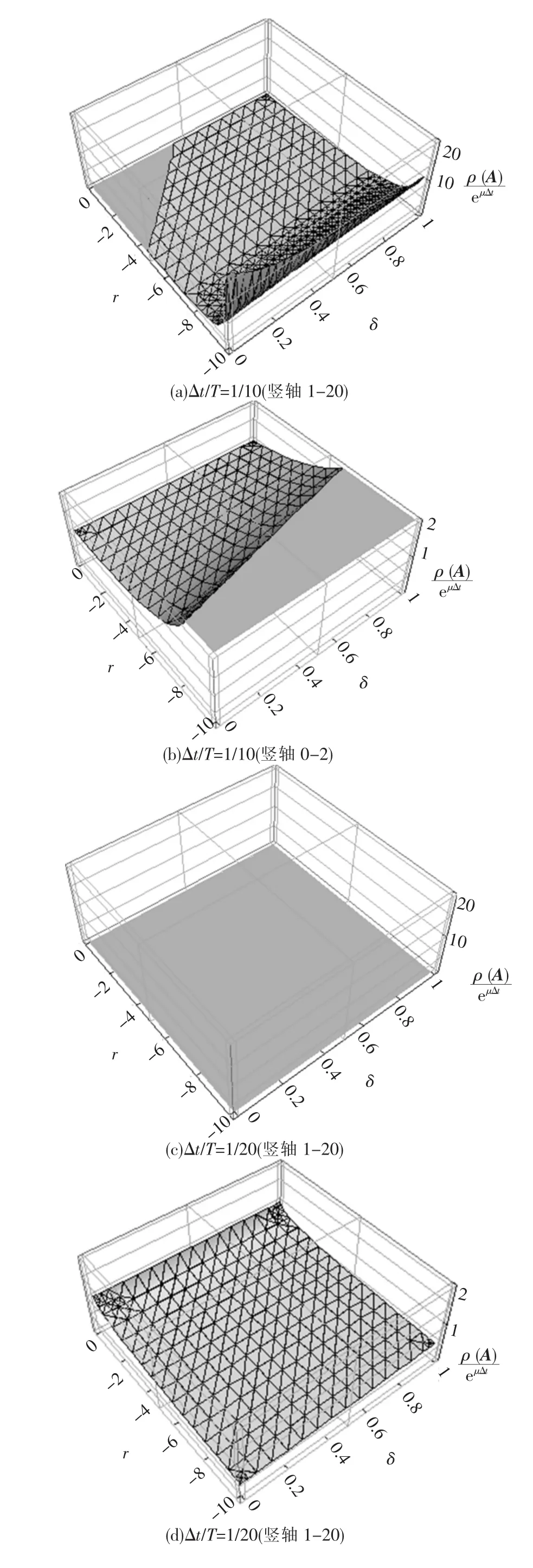
图2 α =1/4、ξ=0.05 时 ρ(A)/eμΔt随 δ的变化

图 3 α =1/4、δ=1/2 时 ρ(A)/eμΔt随 ξ的变化

2.3 分析时间步长的影响

图4为 Newmark参数 α =1/4、δ=1/2、ξ=0.05 时 ρ(A)/eμΔt值随分析步长 Δt/T 以及刚度系数r的变化情况.图4(a)中非网格区域＜ 1，因此有趣的是Δt/T较小时方法却不能保证稳定性，而只有在Δt/T大于某一值时，方法才是稳定的.如果仅从方法稳定性来讲，取大一点的分析步是可以的.但是从计算精度来讲，Δt/T≤0.5时(即一个周期内有2个分析步)才有可能得到准确的结果.同时，对于多自由度体系的分析，Δt/T大于某一值才稳定的方法显然不能同时满足稳定性和准确性的要求，因为对低阶模态满足了稳定性的要求就很难满足高阶模态的准确性要求.此外，稳定区域与不稳定区域之间存在着峰值带.分析方法的稳定性和步长有关，所以并不像正刚度时的无条件稳定，负刚度时Newmark积分方法取α=1/4、δ=1/2是条件稳定的.

图4 α =1/4、δ=1/2时ρ(A)/eμΔt随Δt/T 的变化

3 已有研究的说明

文献［8］通过算例分析指出在负刚度时Newmark方法中参数取值为α=1/4、δ=1/2时精度较低，而参数取值为α=1/12、δ=1/2时得到的结果较好.图5为使用本文方法，针对文献［8］中算例得到的稳定性分析结果，可见对于该算例情况，在 α =1/12、δ=1/2、ξ=0.1、r= －1时积分方法恰好是稳定的，即 ρ(A)/eμΔt值 ＜ 1，而在α =1/4、δ=1/2、ξ=0.1、r=－1时积分方法是不稳定的.图5中同时还给出了参数变化对积分方法稳定性的影响，可见只有在特定的一些情况积分方法才能获得稳定.

图5 参数的不同取值对稳定性的影响

4 方法的合理使用

在正刚度时无条件稳定的Newmark积分方法(α≥(0.5+δ)2/4、δ≥1/2)在负刚度时不再是无条件稳定的.正刚度时被认为精度最好的α=1/4、δ=1/2情况只有在Δt/T大于某一值时才能保证方法稳定.因为难以同时满足稳定性和准确性的要求，所以不适合做具有负刚度的多自由度体系的非线性动力分析.由图1可知，当α取值较小时，Newmark积分方法的稳定性可以保证，因此在实际分析中α可取一小值.一个极端的情况是使用Newmark显式积分方法，即α=0.

5 结语

Newmark积分方法在正刚度时被认为精度最好的α=1/4、δ=1/2情况在负刚度时只有在分析步长大于某一值时才能保证方法稳定性，因此是条件稳定的，同时对于多自由度体系难以同时满足稳定性和准确性的要求.给出了负刚度时Newmark直接积分方法中的参数、阻尼和分析步长等对积分方法稳定性的影响规律.

［1］ BATHE K J.Finite element procedures［M］.New Jersey:Prentice－Hall， 1996，806 － 810.

［2］ 王勖成.有限单元法［M］.北京:清华大学出版社，2003:492－494.

［3］ ZIENKIEWICZ O C，TAYLOR R L，ZHU J Z.The finite element method，Volumn 1:the basis［M］.6th ed.Oxford:Butterworth－Heinemann，2005:606 －611.

［4］ CHOPRA A K.Dynamics of structures:theory and applications to earthquake engineering［M］.2nd ed.Beijing:Tsinghua University Press，2005:174－178.

［5］ 李小军.地震工程中动力方程求解的逐步积分方法［J］.工程力学， 1996，13(2):110－118.

［6］ 刘祥庆，刘晶波，丁桦.时域逐步积分算法稳定性与精度的对比分析［J］.岩石力学与工程学报， 2007，26(S1):3000－3008.

［7］ 程民宪.负刚度条件下数值积分的收敛性和稳定性［J］.力学学报， 1988，20(1):31－40.

［8］ XIE Y M.On the accuracy of time－stepping schemes for dynamic problems with negative stiffness［J］.Communications in Numerical Methods in Engineering， 1993，9(2):131－137.

［9］ 吴云芳.Newmark法在负刚度条件下的收敛性和稳定性［J］.重庆建筑大学学报， 2001，23(1):21－24.

［10］ 程民宪.结构动力分析中几种逐步积分法［J］.工程力学， 1989，6(2):35－47.

On the stability of Newmark integration method for structure with negative stiffness

LI Shuang1，ZHAI Chang－hai1，LIU Hong－bo1，3，XIE Li－li1，2

(1.School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China，shuangli@hit.edu.cn;2.Institute of Engineering Mechanics，China Earthquake Administration，150080 Harbin，China;3.School of Civil Engineering and Architecture，Heilongjiang University，150080 Harbin，China)

To study the applicability of Newmark integration method for structure with negative stiffness，the method is first investigated，and then the numerical stability of the integration method is analyzed.The influences of Newmark integration parameters，damping and time increment on numerical stability of Newmark integration method are also discussed.The result shows that the integration method，which is very different from the case of positive stiffness，is not unconditional numerical stable in the case of negative stiffness.It is found that the usually used Newmark integration method in the case of positive stiffness with α =1/ 4，δ=1/2 is difficult to achieve a balance between stability and accuracy because it is stable only when the time increment lager than a critical value in the case of negative stiffness.The strategy to obtain numerical stability is proposed by selecting appropriate Newmark integration parameters.This paper presents references for applicability of Newmark integration method and selection of rational integration method when structures with negative stiffness.

newmark integration method;negative stiffness;stability;damping;time increment

O241

A

0367－6234(2011)08－0001－05

2010－01－14.

国家自然科学基金资助项目( 90705021，51008101).

李 爽(1981—)，男，博士，讲师;

翟长海(1976—)，男，教授，博士生导师;

谢礼立(1939—)，男，教授，中国工程院院士.

(编辑 赵丽莹)