斜拉索风雨振－实验与数值模拟混合子结构方法

陈文礼，李 惠

(哈尔滨工业大学 土木工程学院，150090哈尔滨，cwl－80@hit．edu．cn)

斜拉索风雨振－实验与数值模拟混合子结构方法

陈文礼，李 惠

(哈尔滨工业大学 土木工程学院，150090哈尔滨，cwl－80@hit．edu．cn)

人工模拟降雨条件下，斜拉索风雨激振的非定常气动力难以测试，本文提出结构风致振动的实验与数值模拟的混合子结构方法，将结构和流场分为2个子结构，将实验获得的结构振动作为动边界施加在流场子结构，仅对动边界的绕流场进行CFD数值模拟．首先通过圆柱涡激振动验证混合子结构方法的可行性及精度;然后采用混合子结构方法，计算斜拉索风雨激振的气动力并施加到斜拉索上，得到斜拉索振动响应并与实验结果比较．结果表明混合子结构方法能够准确获得斜拉索风雨激振的气动力时程．

斜拉索;风雨激振;混合子结构方法;数值模拟

Hikami等［1］在日本 Meiko-Nishi斜拉桥上观测到了斜拉索风雨联合作用下的大幅值振动，峰值最大达到55 cm，此时风速引起的旋涡脱落频率，远大于斜拉索发生涡激振动的频率，因此，将这种振动定义为风雨激振．随后在世界范围内，多个国家的斜拉桥上的斜拉索都发生过风雨激振现象．斜拉索风雨激振是迄今为止发现的振幅最大、危害最严重的斜拉索振动形式之一．Matsumoto等［2］提出风雨激振可由尾流区的轴向流和上水线的形成这2个独立因素分别激发．Verwiebe等［3］认为水线的运动对斜拉索的风雨激振起到关键作用，水线振荡频率与斜拉索振动频率相同．Flamand［4］认为风雨激振是两自由度失稳，只有当水线发生振荡的前提下，拉索才会发生风雨激振．Gu等［5］分析了风偏角、倾斜角、阻尼比及频率对风雨激振的影响，并研究其控制方法．Zhan［6］等通过实验得到斜拉索风雨激振通过螺旋线和增加阻尼的方法可以得到抑制．Coesentino等［7］采用电阻法测量斜拉索表面的水线运动特征．Li等［8］通过超声波测厚系统对斜拉索风雨激振时其表面的水线几何与动力进行了定量测量与分析．由于试验技术的限制，作用于斜拉索上的气动力难以测试，而气动力分析是揭示斜拉索风雨激振机理的重要手段．考虑到风洞试验中，结构振动易于测量，但流场的风压分布较难测试．为此，本文提出实验与数值模拟的混合子结构方法，即将结构和流场分为2个子结构，结构振动通过实验获得，并作为动边界施加在流场子结构，仅采用CFD数值模拟方法计算动边界的绕流场特性．由于该方法不需进行结构有限元计算和数据交换，可以极大地提高结构风致振动的计算效率;同时由于结构振动是在斜拉索风雨激振的风洞试验中测到的，测到的斜拉索振动反映了流场和斜拉索之间相互作用，因此，绕流场特性的数值计算结果具有较高精度．

首先通过圆柱涡激振动来验证混合子结构方法的可行性及精度;随后，通过风洞试验得到斜拉索和水线动边界的运动时程，采用混合子结构方法，计算斜拉索风雨激振的气动力并施加到斜拉索模型上，得到斜拉索的振动响应并与试验结果进行比较分析．

1 混合子结构方法的数值验证

1.1 验证模型

为了验证混合子结构方法的可行性与精度，本文将其与传统流固耦合方法进行比较，二者的区别在于:采用流固耦合方法时，流场特性与结构振动都通过计算得到，混合子结构方法只模拟动边界(实验得到)的绕流场特性．采用二维圆柱涡激振动对混合子结构方法的可行性及精度进行数值验证．图1为二维圆柱涡激振动的CFD数值模拟的流场计算区域和划分的网格．圆柱中心距上游边界10 D，距下游边界40 D，离上下边界各为10 D，D为与来流方向垂直的特征长度(圆柱直径)，本文D=0.01 m．边界条件设置如下:左侧空气流入，采用速度入口边界(velocity inlet)，来流为均匀速度;右侧空气流出，采用完全发展出流边界(outflow);上下边界:采用自由滑移壁面(symmetry);圆柱表面:无滑移边界条件(wall)，即圆柱表面的流体速度等于圆柱的运动速度，圆柱的运动速度通过用户自定义函数(UDFs)中的动网格运动宏来赋值．

图1 流场计算区域与网格划分

圆柱为弹性支撑，将圆柱振动简化为质量－弹簧－阻尼系统．单位长度圆柱的质量、刚度和阻尼系数分别为mcyl、kcyl和ccyl;自振频率为fcyl，圆柱固定绕流的旋涡脱落频率为fvox．文献［9］采用Fluent对低雷诺数(Re=200)下弹性圆柱涡激振动进行了流固耦合方法的CFD数值模拟(湍流模型为SST k－ω)，得到了频率比为1.15时，圆柱的振动响应和气动力系数．如图1所示，将圆柱作为结构子结构，通过用户自定义函数(UDFs)将流固耦合方法得到的位移施加到圆柱的边界上，使其成为动边界，通过Fluent对动边界(圆柱)进行绕流数值模拟(湍流模型为SST k－ω)，并将混合子结构方法与流固耦合方法得到的气动力系数时程进行比较分析．

1.2 混合子结构方法验证结果分析

流固耦合方法与混合子结构方法得到的气动升力系数和阻力系数分别为 Cl－VIV，Cd－VIV和Cl－FV，Cd－FV．图 2 表示2 种方法得到的气动力系数比较，可以看出不管是升力系数还是阻力系数，2种方法得到的结果非常接近，说明2种方法在气动力的计算上是等效的．

将混合子结构方法得到的气动升力Fl－FV施加到圆柱上，通过圆柱单自由度运动方程得到其振动位移，并与流固耦合方法得到的圆柱位移时程进行比较分析．圆柱横风向振动的单自由度运动方程为

式中:ρ为空气密度，取1.225 kg/m3，U为流场入口处风速．采用Newmark-β对式(1)进行求解，得到圆柱振动的位移时程，并与流固耦合方法得到的圆柱振动位移进行比较，如图3所示，两者吻合很好．由于2种方法得到的气动力系数接近，因此其振动响应也是吻合的．

图2 频率比为1．15时2种方法气动力系数比较

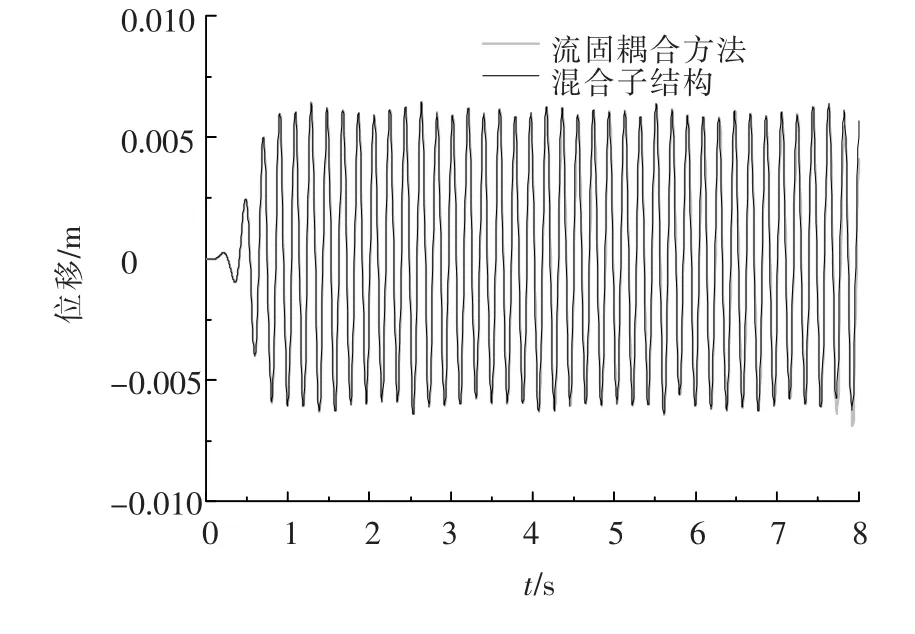
图3 圆柱振动位移的比较

接下来对2种数值模拟方法得到的圆柱尾流旋涡脱落的模式进行分析，选取2.5 s时刻的涡量等值线图进行比较分析，如图4所示．2种数值模拟方法得到的圆柱尾流旋涡脱落的模式是一致的，都是2S结构;而且旋涡脱落的过程几乎一样，只是在较远处存在轻微差别．

图4 2种方法涡量等值线图比较

综上所述，采用本文提出的混合子结构方法模拟圆柱涡激振动，其计算得到的气动力系数、圆柱的振动响应以及圆柱的尾流旋涡结构都与流固耦合方法的计算结果吻合很好，表明混合子结构方法计算圆柱涡激振动的绕流场特性及其气动力是可行的．由于混合子结构方法仅计算流场部分，与流固耦合方法还需要计算结构部分计算及流场与结构模型之间的数据传递相比，计算时间较大缩短(采用同样4核CPU的PC机，计算本文8 s的时程，流固耦合方法需用时约8 h，混合子结构需用时约7 h)，因此混合子结构方法的计算效率要高;而且结构越复杂、单元越多，混合子结构方法的效率相对流固耦合方法的优势越明显．

2 斜拉索风雨激振的三维混合数值模拟子结构方法

2.1 三维混合子结构方法的模型

斜拉索节段模型风雨激振的风洞试验是在同济大学土木工程防灾国家重点实验室TJ1大气边界层风洞中完成的．风洞试验段1.8 m×1.8 m×12 m，风速1～30 m/s．风雨激振的试验装置位于风洞的出口处，是由同济大学葛耀君教授在顾明教授［5］试验装置的基础上改造而来的，由支架和人工降雨装置2部分组成，如图5所示．

人工降雨装置能实现强度从10～70 mm/h连续可调．节段模型在风场中倾斜放置，风速斜向下吹向节段模型，α为节段模型的倾斜角，β为节段模型的风偏角．斜拉索节段模型总重17.15 kg，其振动采用加速度传感器测试，采样频率为50 Hz．2个加速度传感器分别安置在模型两端用来测量模型横风向响应．斜拉索模型横风向自振频率和阻尼比分别为0.952 Hz和0.17%．图6表示斜拉索模型横风向振动幅值随风速的变化，两次试验的倾斜角30°，风偏角分别为20°和22.5°．通过比较发现，两次试验得到的风洞试验结果接近，这两次试验不仅测量得到风雨激振斜拉索的振动响应，而且同步测试到水线的信号，水线振动信息通过超声波测厚系统得到［10］．

图5 试验装置

对斜拉索风雨激振进行三维子结构方法的CFD数值模拟，取发生风雨激振的风速点(7.72 m/s)进行分析，此时在斜拉索表面会形成通长的上水线，图7和图8分别表示斜拉索振动和上水线振荡响应，二者主导频率都等于斜拉索自振频率．

图6 斜拉索模型横风向振动幅值随风速的变化

斜拉索与水线的动边界设置如下:斜拉索边界按照风洞试验实测的振动做横风向运动(如图7(a)所示);水线跟随斜拉索模型边界做横风向振动的同时，沿着拉索模型边界做环向振荡(如图8(a)所示)，因此系统由流场子结构、上水线子结构和斜拉索子结构3部分组成．斜拉索与上水线模型如图9所示，风向为垂直纸面向里，上水线截面尺寸采用文献［10］中超声波测厚系统得到的近似梯形(水线厚度与底边分别为0.5 mm和8 mm，底角45°)，并假设沿斜拉索长度方向尺寸与形状保持不变．

2.2 三维混合子结构方法的计算结果分析

通过三维混合子结构方法得到斜拉索发生风雨激振(7.72 m/s)时，其气动力系数(升力系数和阻力系数)如图10和图11所示，气动力系数的主导频率等于斜拉索自振频率．

图7 风速7．72 m/s时斜拉索风雨激振横风向的振动响应

图8 风速7．72 m/s时斜拉索上水线沿环向的振动响应

图9 斜拉索、水线模型及网格划分

图10 工况2斜拉索模型升力系数

将混合子结构方法得到的气动力系数施加到斜拉索模型上，通过Newmark-β法对式(1)进行数值求解，得到斜拉索节段模型横风向振动响应，如图12所示．通过与风洞试验结果(图7)进行对比可知，数值求解结果与风洞试验结果较为接近，这也说明混合子结构方法能够准确地求解出斜拉索发生风雨激振时其受到的气动力．

目前国内很多大跨度桥梁结构和超高层建筑结构都已经安装健康监测系统，能够准确地获得结构振动信息和结构所处风场的风速时程信息，但是目前的健康监测系统较难获得这些结构的气动力，而可以结合物理实验(现场健康监测或风洞试验)与CFD数值模拟二者优势，根据结构振动时程和风速时程信息，通过采用混合子结构方法来求得结构的气动力．

图11 工况2斜拉索模型阻力系数

图12 斜拉索横风向振动时程

3 结论

1)通过与圆柱涡激振动流固耦合方法得到的气动力系数、圆柱振动响应、尾流结构、以及计算时间4方面进行对比，验证了混合子结构方法的计算结果与流固耦合方法吻合很好、具有更高的计算效率．

2)混合子结构方法能够准确地计算斜拉索发生风雨激振时其受到的气动力，子结构方法得到的斜拉索振动响应与风洞试验结果接近，说明混合子结构得到的气动力具有较高的精度．

3)在获得结构振动时程与所处风场风速时程前提下，混合子结构方法可适应于桥梁及高层建筑等结构发生明显风致振动时气动力的求解．

致谢

试验研究工作在同济大学防灾减灾国家重点实验室完成，衷心感谢同济大学桥梁工程系的葛耀君教授和赵林博士的支持、帮助与指导，感谢哈尔滨焊接研究所张锐副研究员对试验的帮助．

［1］ HIKAMI Y，SHIRAISHI N．Rain-wind-induced vibrations of cables in cable stayed bridges［J］．Journal of Wind Engineering and Industrial Aerodynamics， 1988，29:409－418．

［2］ MATSUMOTO M，SHIRASHI N，SHIRATO H．Rainwind induced vibration of stay-cables of cable-stayed bridges［J］．Journal of Wind Engineering and Industrial Aerodynamics， 1992，41/42/43/44:2011－2022．

［3］ VERWIEBE C，RUSCHEWEYH H．Recent research results concerning the exciting mechanisms of rainwind-induced vibrations［J］．Journal of Wind Engineering and Industrial Aerodynamics， 1998，74/75/76:1005－1013．

［4］ FLAMAND O．Rain-wind-induced vibration of cables［J］．Journal of Wind Engineering and Industrial Aerodynamics， 1995，57:353 －362．

［5］ GU Ming，DU Xiaoqing．Experimental investigation of rain-wind-induced vibration of cables in cable-stayed bridges and its mitigation［J］．Journal of Wind Engineering and Industrial Aerodynamics， 2005，93:79 －95．

［6］ ZHAN S，XU Y L，ZHOU H J，et al.Experimental study of wind-rain-induced cable vibration，2008［J］．Journal of Wind Engineering and Industrial Aerodynamics， 2008，96:2438 －2451．

［7］ COESENTINO N，FLAMAND O，CECCOLI C．Rainwind-induced vibration of inclined stay cables Part I:experimental investigation and physical explanation［J］．Wind and Structures， 2003，6(6):471 －484．

［8］ LI Fengchen，CHEN Wenli，LI Hui，et al.An ultrasonic transmission thickness measurement system for study of water rivulets characteristics of stay cables suffering from wind-rain-induced vibration［J］．Sensors and Actuators A:Physical， 2010，159(1):12 －23．

［9］ 徐枫，欧进萍，肖仪清．不同截面形状柱体风致振动的CFD数值模拟［C］//第十三届全国结构风工程学术会议论文集(下册)．大连:大连理工大学，2007:1042－1048．

［10］ 陈文礼，李惠，李凤臣．斜拉索风雨激振水线的超声波测试系统［J］．地震工程与工程振动， 2009，29(1):139－145．

Hybrid approach combining experiment and CFD numerical Simulation for rain-wind-induced vibration of a stay cable

CHEN Wen-li，LI Hui

(School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China，cwl－80@hit．edu．cn)

As the aerodynamic forces are inconvenient to be measured in the wind tunnel tests of rain-wind-induced vibration(RWIV)of a stay cable under artificial simulation of rainfall，this paper presents a hybrid approach combining experiment and computational fluid dynamics(CFD)numerical simulation for RWIV of a stay cable．The stay cable(including the rivulet)and the flow field are considered as two substructures in the entire system，and the motions of stay cable and rivulet measured through wind tunnel tests are considered as known boundary condition and applied to the flow field．The flow around the moving boundary is then numerically simulated by the Fluent CFD code．First，the feasibility and precision of this approach are verified through the vortex-induced vibration of a circular cylinder，and then the approach is used to study the RWIV of the stay cable．The transient aerodynamic lift and drag coefficients are calculated and applied to a single degree of freedom model(SDOF)of the stay cable．The comparison is carried out between the oscillation responses of the SDOF model and experimental results，which indicate that the hybrid approach combining experiment and CFD numerical simulation can effectively simulate the transient aerodynamic coefficients of stay cable suffering from the RWIV．

stay cable;rain-wind-induced vibration;hybrid approach;numerical simulation

TU352.2;TU311.3

A

0367－6234(2011)08－0006－05

2010－04－01．

国家自然科学基金青年科学基金(51008093);国家自然科学基金重点项目(90815022);哈尔滨工业大学科研创新基金资助项目(HIT．NSRIF．2009099)．

陈文礼(1980—)，男，博士，讲师;

李 惠(1966—)，女，教授，博士生导师．

(编辑 赵丽莹)