基于SVDD的全国科技进步聚类分析

赵成，肖健华

（五邑大学 经济管理学院，广东 江门 529020）

基于SVDD的全国科技进步聚类分析

赵成1，肖健华2

（五邑大学 经济管理学院，广东 江门 529020）

科技进步是国家经济发展的强大动力和坚实基础，是影响国家综合国力和国际竞争力的决定性因素. 论文选取2008年中国31个省市科技进步综合指标评价数据，先标准化处理这些数据，再采用因子分析法对样本进行降维，最后用支持向量数据描述模型聚类分析了2008年全国科技进步的情况.

科技进步；因子分析；支持向量数据描述

科技进步是指国家坚持科学发展观，实施科教兴国战略，实行自主创新、重点跨越、支撑发展、引领未来的科学技术工作指导方针，构建国家创新体系，建设创新型国家.[1]进入新世纪，世界各国政府都在思考和部署新的经济与社会发展战略. 中国作为世界上最大的发展中国家，为了保持经济的持续快速健康发展，必须把加快科技进步和创新置于经济与社会发展的优先地位. 本文借鉴国内学者已有的研究成果，选取2008年全国31个省市科技进步综合指标评价数据（见中国国家统计局网站http://www.most.gov.cn/kjtj/tjbg/200907/P020090729400672549276.pdf），以“科技进步评价指标体系”的5个综合指标（科技进步环境指数x1、科技促进经济社会发展指数x2、科技活动投入指数x3、科技活动产出指数x4和高新技术产业化指数x5，具体见中国国家统计局网站http://www.most.gov.cn/kjtj/ tjbg/200806/P020090731393749062749.pdf）为原变量，先用因子分析法[2]对其降维，再用支持向量数据描述算法（support vector data description，SVDD）对其进行聚类分析.

1 SVDD的聚类方法

对于数据对象的样本集X={x1,x2,…xn}，SVDD的聚类方法就是通过寻找一个半径最小的超球体把所有样本包围起来，数据描述的优化问题可以表示为：

其中R为样本集中全体样本完全包围所对应的最小球体的半径，a为最小球体的球心.

由式（1）和式（2）可得Lagrange函数：

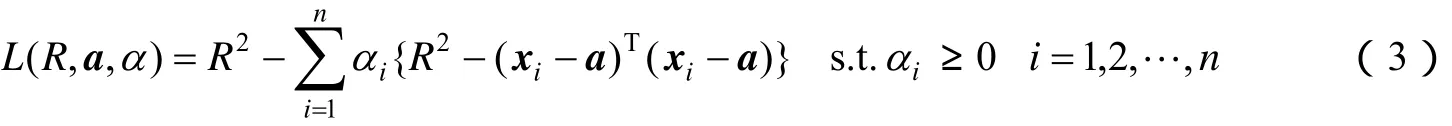
对式（3）中的R和a求偏微分并令它们等于0，可得：

由式（3～5），经过简化，得：

此时，与αi＞0的这部分相对应的样本点构成了样本的边界，将此样本点称为支持向量. 这时求出来的超球体可能失真，即所形成的区域不能准确地反映实际样本数据的分布特征，为此我们在上述优化过程中引入核方法[3]，即将(x1·x2)→K(x1,x2)代入式（6），得：

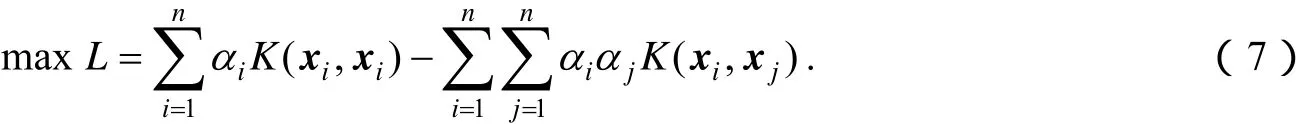
结合本文需要将核函数具体化，选取高斯径向基核函数：

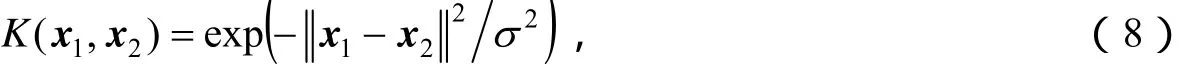
则式（7）可表示成：

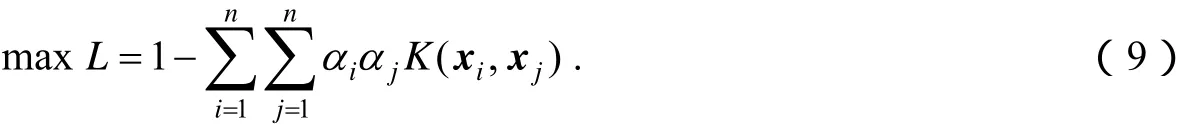
由此可见，引入高斯径向基核函数在数据空间中可获得较为理想的数据描述边界.

对于同一个三维一类样本分布，若采用常规方法进行数据描述，其结果如图1-a所示；若以高斯径向基核函数作为核函数进行数据描述，其结果如图1-b所示. 可见采用核方法可获得较为理想的数据描述边界.

图1 不同方法下获得的数据描述边界

2 科技进步的评价

2.1 科技进步评价指标的降维

对于原始数据，由于不同指标的评价标准不同，因此不同指标间的数量级相差很大，为了排除数量级和量纲不同带来的影响，首先对原始数据进行标准化处理.

设有n个样本，p项指标，可得数据矩阵X=(xij)n×p,i=1,2,…,n ；j=1,2,…,p；xij表示第i个样本的第j项指标值. 对数据进行标准化变换：

2008年全国31个省市科技进步综合评价数据标准化的结果见表1.

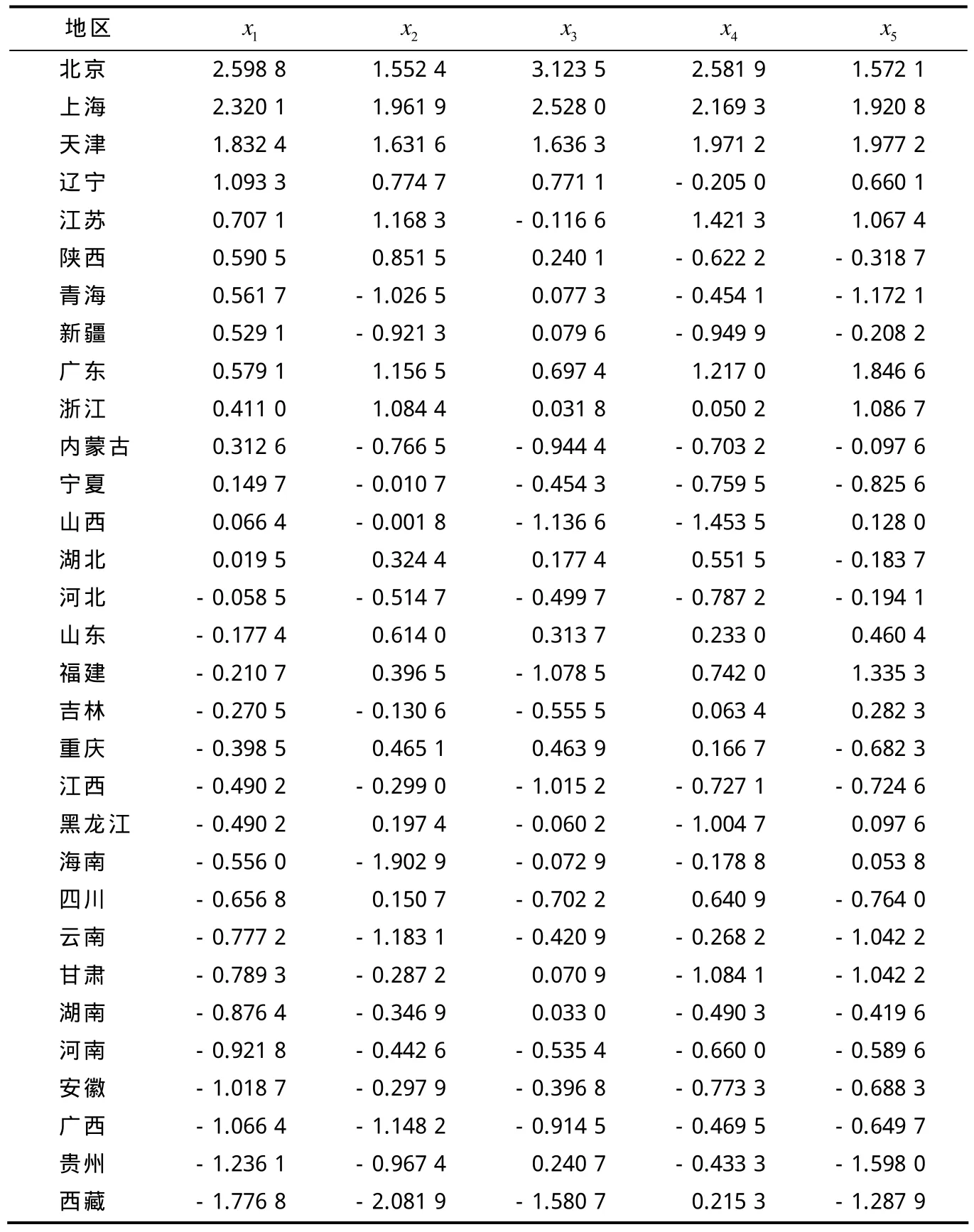
表1 5个综合指标原始数据标准化的结果

根据因子分析方法的原理，运用统计软件可计算出各因子所对应的特征值、贡献率、累计贡献率与各指标变量方差最大(Varimax)正交旋转后的因子载荷矩阵等，5个评价指标的因子总方差分析如表2所示. 根据因子累计方差贡献率超过85%的原则，从表2可以得出：提取x1和x2两个主成分已足以表达原始数据的绝大多数信息.[4]故只选取科技进步环境指数、科技促进经济社会发展指数2个变量，原始数据降维后的结果见表3.

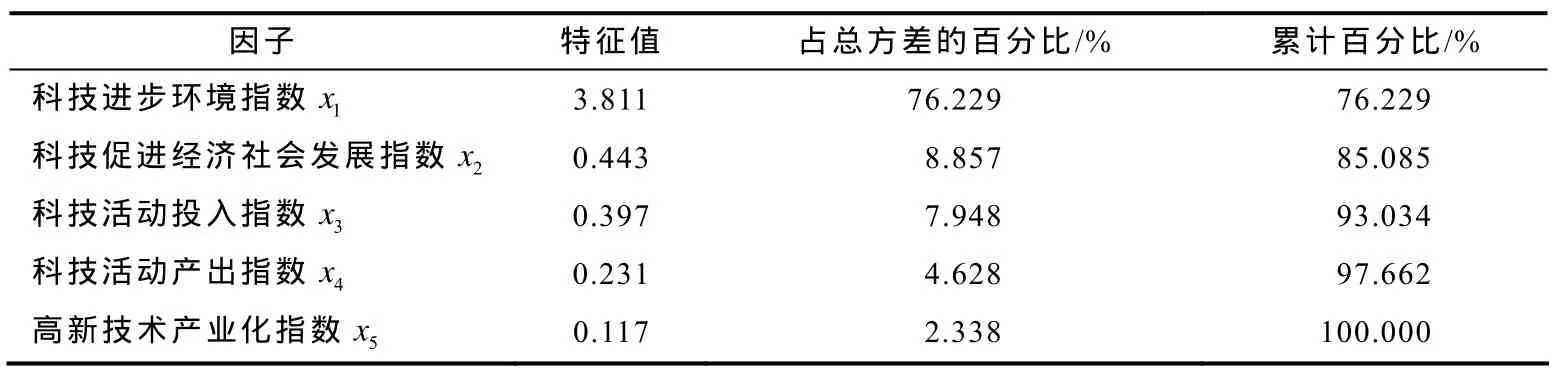
表2 因子总方差表

表3 科技进步评价指标降维后的结果

2.2 科技进步的SVDD评价

选择高斯径向基核函数，对表3中数据进行聚类分析，所得结果如图2所示.

分析图2可大致得出：1）上海、北京为第1类，科技进步水平最强；2）天津为第2类，科技进步水平较强；3）广东、江苏、浙江、辽宁为第3类，科技进步水平为强；4）山东、福建、陕西、湖北、重庆、吉林、黑龙江、四川、新疆、湖南、宁夏、河北、山西、内蒙古、青海、甘肃、安徽、河南、海南、江西、贵州、云南和广西为第4类，科技进步水平一般；5）西藏为第5类，科技进步水平最低. 此分类结果与原始分类十分吻合.

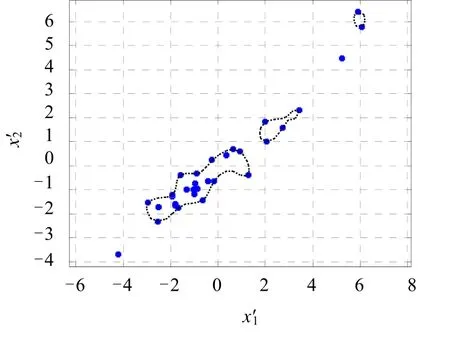
图2 区域科技进步SVDD评价结果

总体上看，科技进步与经济发展程度有较强的相关性[5]. 作为第1类的北京、上海，科技进步最强，同时二者也是全国经济科技发展水平最高的地区，其中北京市的科技活动产出和科技活动投入稳居全国首位，但企业创新较弱，倾向于从国外获取技术. 为此，北京市应提高企业科技创新能力，加强北京本地企业与高校、研究机构的合作. 上海市各方面优势都很明显，政府、企业科技投入都很高，高科技产业发达、技术市场兴盛，国际合作很多，产学研水平很高，跨国公司是上海市企业发展研发的主体，但本地企业研发水平较低. 作为单独一类的天津，近些年经济发展速度快，政府科技投入大，经济发展得益于外资作用，其科技进步强的重要原因是位于沿海地区，其改革开放领先于全国并为科技进步提供了良好的体制框架和市场经济体系. 作为第3类的广东、江苏、浙江、辽宁归为一类，其科技进步得益于地处沿海地区以及国家（对东北老工业基地）的政策扶持，其中广东经济发达，宏观经济水平、产业结构水平、产业竞争力和就业水平等均位居全国首位，政府、企业对科技投入绝对量大，但是总体研发强度较低，使得科技进步发展与经济发展不符. 其余省份地处内地，在开放程度、政策支持、政府企业对科技投入力度等方面均不高，使得科技进步发展普遍较低.

3 结语

本文借助SVDD对全国科技进步进行聚类分析，克服了传统定量方法所采用的线性排序的不足.传统线性排序在确定指标权重的时候经常依赖于决策者的主观经验，往往未能客观地反映各指标的主次性，借助SVDD实现各地区科技进步的聚类，不仅更客观地综合了科技进步各方面的信息，而且聚类结果更形象合理，可以给决策者提供精准的决策依据.

[1] 全国人民代表大会常务委员会. 中华人民共和国科学技术进步法[M]. 北京：中国法制出版社，2008.

[2] 仲生仁. 因子分析方法及其在教学管理中的应用[D]. 兰州：兰州大学，2007.

[3] MULLER K R, MIKA S, RATSCHG, et al. An introduction to kernel-based learning algorithms[J]. IEEE Trans on Neural Networks, 2001, 12(2): 181-201.

[4] 蒋惠园，王晚香. 主成分分析法在综合评价中的应用[J]. 武汉理工大学学报：交通科学与工程版，2004, 28(03): 467-470.

[5] 佚名. 2000全国科技进步综合评价[J]. 科技统计，2002, 3(5): 27-29.

A SVDD-based Cluster Analysis of National Scientific and Technological Advancement

ZHAO Cheng1, XIAO Jian-hua2
(Wuyi University Economic Management School, Jiangmen 529020, China)

The scientific and technological progress of a country is a strong driving force and solid foundation for its economic development and decides the comprehensive national strength and international competitiveness. This paper selects the comprehensive index evaluation data of China’s 31 provinces, autonomous regions and municipalities in the year 2008 for science and technology progress evaluation and standard-processed the data in light of “science and technology advancement evaluation index system”. Then the paper uses the factor analysis to reduce the dimensions of the original data and the support vector data description model to evaluate the national scientific and technological progress of China in the year 2008.

scientific technological progress; factor analysis; support vector data description

G642.0；O29

A

1006-7302（2011）01-0065-05

2010-05-10

赵成（1984—），男，山东高唐人，硕士研究生，研究方向为电子商务；肖健华，教授，博士，硕士生导师，通信作者，研究方向为人工智能理论与应用.