全纯函数的正规族与分担集

徐俊峰

（五邑大学 数学与计算科学学院，广东 江门 529020）

全纯函数的正规族与分担集

徐俊峰

（五邑大学 数学与计算科学学院，广东 江门 529020）

利用分担集合的思想证明了定理：设F是单位圆盘内的一族全纯函数族，a1和a2是2个不同的有限复数且a1+a2≠0；当α≥1时，如果对于任意的f∈F，Ef(S)=Ef＇(S)，S={a1,a2}在单位圆内成立，那么f是一个α-正规函数.

全纯函数；亚纯函数；正规函数；分担集

1 引言及主要结果

设D是复平面的区域，F是区域D中的一族亚纯函数. 在Montel意义下，如果F的子序列{fn}中包含一列子序列{fnj}，且其在D内一致局部球形收敛到一个亚纯函数或者无穷，则称F在区域D内正规.[1]

本文假设f,g是区域D内的2个亚纯函数，S1和S2是2个集合. 如果f(z)∈S1⇒g(z)∈S2，则记为f(S1)⊂g(S2). 如果f(z)∈S1⇔g(z)∈S2，则记为f(S1)=g(S2). 类似地，如果f(z)∈S1⇔g(z)∈S2，则记为Ef(S1)=Eg(S2). 如果集合S只有1个元素a，我们用f(z)=a表示f(z)∈S.[2]

Schwick[3]首先将函数族F（和它们的导数）的分担值与其正规性联系起来，并证明了：对每一个f∈F，以及区域D内的3个不同复数a1,a2,a3，如果f和f＇分担a1,a2,a3，那么函数族F在区域D内正规.

庞学诚等[4]325推广了这个结果，得到定理A.

定理A 设F是区域D中的一族亚纯函数族，a,b,c,d是复常数且满足c≠a和d≠b. 如果对每一个f∈F，有f(z)=a⇔f＇(z)=b和f(z)=c⇔f＇(z)=d，那么F在区域D内正规.

定义1[5-6]一个亚纯函数f是单位圆D内的正规函数当且仅当这里存在一个常数 C(f)（此常数仅与f有关）使得(1-|z|2)f♯(z)＜C(f)，这里f♯(z)=|f＇(z)|/(1+|f(z )|2)是f的球形导数.

2000年，庞学诚[7]602利用分担值考虑正规函数，得到定理B.

定理B 设F是单位圆中的一族亚纯函数族，a1,a2,a3是3个不同的有限数. 如果对每一个f∈F，f(ai)=f＇(ai)，i=1,2,3，在单位圆内成立，则存在一个正数M（M仅与a1,a2,a3有关），使得对每一个f∈F，有(1-|z|2)f♯(z)＜M .

事实上，由定理B可以得到下面的推论.

推论1 设F是单位圆中的一族全纯函数族，a1,a2是2个不同的有限复数，如果对每一个f∈F，f(ai)=f＇(ai)，i=1,2，在单位圆内成立，则定理B的结论成立.

最近，许多学者利用分担集合来研究正规族[7-9]，如刘晓俊[9]411利用分担集合S={a1,a2,a3}得到一个类似于定理B的正规族，那么利用分担集合S={a1,a2}能否得到类似推论1的正规族是一个令人感兴趣的问题. 本文利用文献[10]的方法研究了这个问题并得到下面的结果.

定理1 设F是单位圆中的一族全纯函数族，a1,a2是2个不同的有限复数，且a1+a2≠0. 如果对每一个f∈F，Ef(S)=Ef＇(S )，S={a1,a2}在单位圆内成立，则存在一个正数M(M仅与a1,a2,a3有关)，使得对每一个f∈F，有（1-|z|2）f♯(z)＜M .

下面举例说明条件a1+a2≠0是必要的.

例1[10]1214设S={-1,1}. 令F={fn(z):n =2,3,4…}，这里，那么对任意的fn∈F，有n2[fn2(z)-1]=fn2＇(z )-1；因而fn和fn＇分担集合SCM，但是fn在D内不正规.

推论2 设F是单位圆中的一族全纯函数族，a是一个非零的有限复数，如果对每一个f∈F，f和f＇分担集合S={0,a}IM在单位圆成立，那么定理1的结论成立.

例2说明条件中复数a为有限数也是必要的.

例2 设S={0,∞}. 令F={enz:n=1,2…}，D={z:|z|＜1}，那么fn=enz且fn＇=nenz分担集合SIM，但是fn在D内不正规.

定义2[11-13]给定0＜α＜∞，如果存在一个常数Cα(f)使（1-|z|2）αf♯(z)＜Cα(f )，则称f是单位圆D内的α-正规函数.

定理2 令α≥1. 设F是单位圆中的一族全纯函数族，a1,a2是2个不同的有限复数，且a1+a2≠0. 如果对每一个f∈F，Ef(S)=Ef＇(S )，S={a1,a2}在单位圆内成立，则存在一个正数M(M仅与a1,a2,a3有关)，使得对每一个f∈F，有（1-|z|2）αf♯(z)＜M.

2 引理

引理1[4]328设F是定义在单位圆Δ内的亚纯函数族，对于F中的任意函数f，其零点重数至少为k，f（z）=0⇒|f(k)(z)|≤A. 如果F在单位圆Δ内不正规，那么对0≤α≤k，存在一个点列zn,zn＜r＜1，一个函数列fn∈F，以及正数列ρn→0+使得按球面距离内闭一致收敛到非常数亚纯函数g(ξ)且满足g#(ξ)≤g#(0)=kA+1.

引理2 设F是定义在单位圆Δ内的亚纯函数族，对于F中的任意函数f，其零点重数至少为k，f（z）=0⇒|f(k)(z)|≤A. 如果F不是α-正规函数，那么对0≤α≤k和1≤α＜∞，这里存在一个点列zn,zn＜r＜1和一个正数序列ρn→0+，以及函数列fn∈F使得{gn(ζ)}=ρn-λf（zn+(1-|zn|2)αρnζ ）按球面距离内闭一致收敛到ζ平面上的一个非常数Yosida函数.

采用文献[12]的方法可以证明上述引理.

3 定理2的证明

假设结论不成立，可以找到序列zn＜1和函数列fn∈F使得gn(z)=fn（zn+(1-|zn|2)αz）满足：

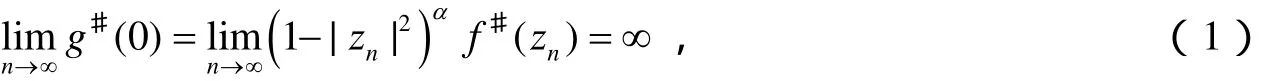
因而，{gn(z)}在单位圆内不正规.

由引理2可以找到正数r，0＜r＜1；复数ζn，|ζn|＜1；ρn→0+和gn∈F使得Gn(ζ)=gn(ζn+ρnζ)= fn（zn+(1-|zn|2)αζn+(1-|zn|2)αρnζ ）局部一致地收敛到一个非常数的整函数G(ζ). 由于G是一个非常数整函数，不失一般性，假设G-a1在复平面有零点，设ζ0是G-a1的零点.考虑亚纯函数族

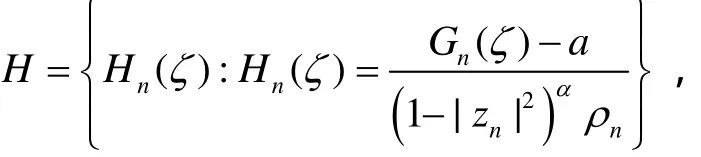
我们断言H在点ζ0不正规.

事实上，要么G(ζ0)=a1，要么G(ζ)≡/a1.由式（1）和Hurwitz定理，如果这里存在ζn满足ζn→ζ0，Gn(ζn)=a1，那么Hn(ζn)=0. 然而，这里存在一个正数δ使得Δδ={z∈D:0＜|ζ-ζ0|＜δ}⊂D，但在Δδ内G(ζ)≠a1，因而对每一个ζ∈Δδ，Gn(ζ)≠a1（当n充分大）；从而对每一个ζ∈Δδ，有H(ζ)=∞.这样就证明了H在点ζ0不正规.

注意到Hn(ζ)=0⇒(ζ)=a1或a2，再利用引理2，可以得到τn→τ0，ηn→0以及Hn∈H使得

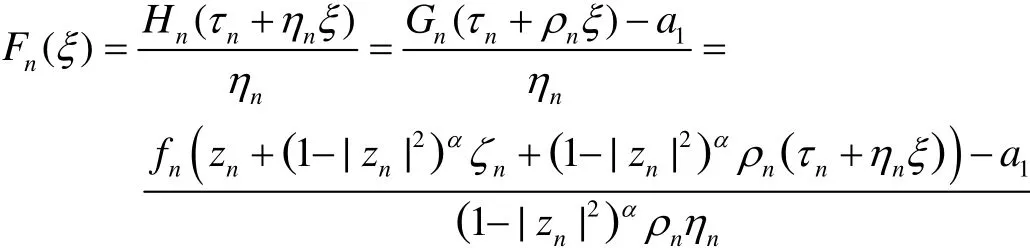
局部一致地收敛到一个非常数整函数F(ξ)，且F♯(ξ)≤F♯(0)=M.特别地，ρ(F)≤1.

我们断言：

1）F只有有限多个零点.

2）F(ξ)=0⇔F＇(ξ)=a1或a2.

证明 对于断言1）.假设ζ0是G(ζ)-a1的k重零点，如果F(ξ)有无穷多个零点，那么这里存在k+1个不同的点ξj(j=1,…,k+1)满足F(ξj)=0(j=1,…,k+1).注意到F(ξ)≡/0，由Hurwitz定理，这里存在整数N，如果n＞N，则有F(ξj)=0(j=1,…,k+1)和Gn(τn+ηnξjn)-a1=0，于是

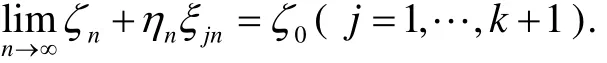
即ζ0是G(ζ)-a1的至少k+1重零点，这与ζ0是G(ζ)-a1的k重零点矛盾，于是断言1）得证.

对于断言2）.假设F(ξ0)=0，那么由Hurwitz定理，这里存在ξn,ξn→ξ0（当n充分大），使得

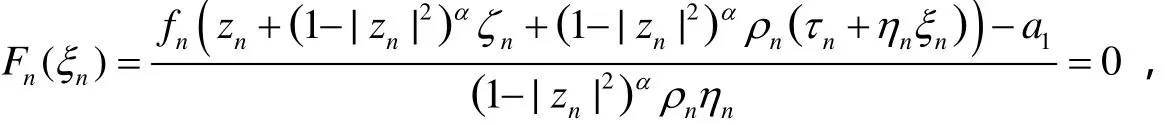
因而，fn（zn+(1-|zn|2)αζn+(1-|zn|2)αρn(τn+ηnξn)）=a1.由假设，有：

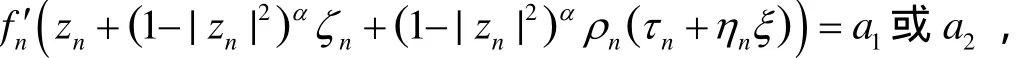
因而，

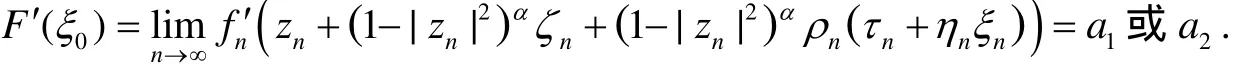
这就证明了F(ξ)=0⇒F＇(ξ)=a1或a2.

下面再证明F＇(ξ)=a1或a2⇒F(ξ)=0.

假设F＇(ξ0)=a1.明显地，F＇≡/a1，否则F♯(0)≤|F＇(0)|=|a1|＜M，矛盾.然后由Hurwitz定理，这里存在ξn,ξn→ξ0（当n充分大），使得

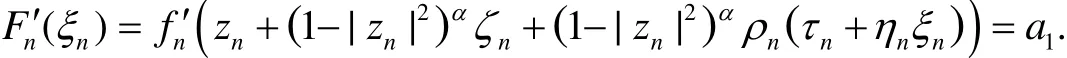
从而，

如果这里存在一个正整数N，则对每一个n＞N，有：

从而，

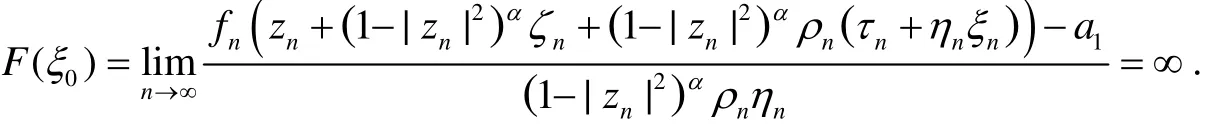
这与F＇(ξ0)=a1矛盾.因而这里存在{fn}的一个子序列（通过重排，我们继续用{fn}表示）满足fn（zn+(1-|zn|2)αζn+(1-|zn|2)αρn(τn+ηnξn)）=a1.于是，得到

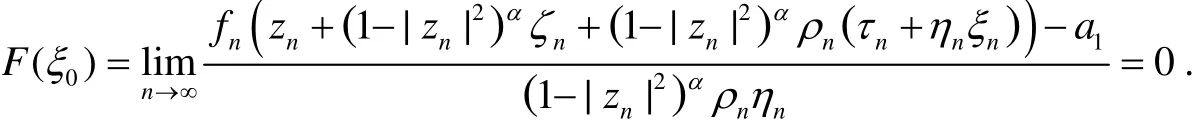
这就暗含F＇=a⇒F=0.

类似地，我们得到F＇=a2⇒F=0，从而证明了断言2）.

由于ρ(F＇)=ρ(F)≤1，那么由Nevanlinna第二基本定理有：

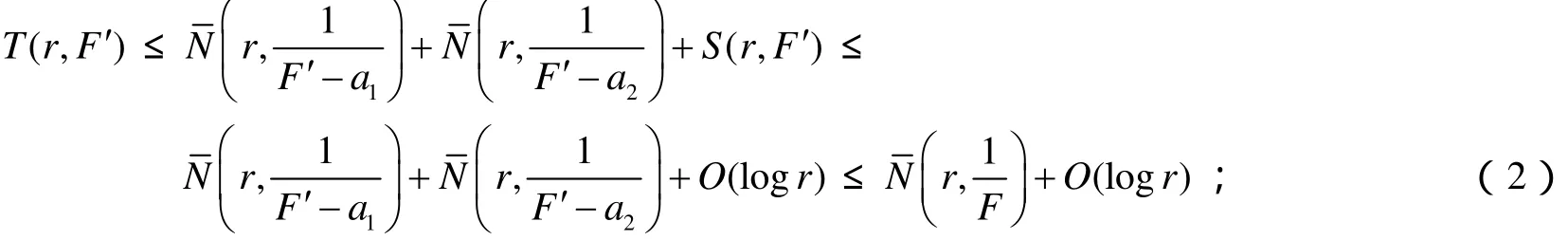
情况1 a1a2=0. 不失一般性，假设a1=0. 我们知道F＇有零点，那么F有重零点. 假设deg(F)=n，那么T(r,F＇)=(n-1)log r 和S(r,F＇)=O(1). 由式（2），有：

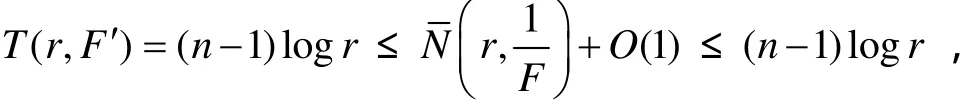
因而得到F只有重零点且其重数为2，F＇只有1个单零点，这就推出n=2. 令F＇=B(ξ-ξ0)，那么，这与F＇=a2⇒F=0矛盾. 证毕.

情况2 a1a2≠0. 我们首先证明F=0⇔F＇=a1或a2. 由a1a2≠0，得到F=0→F＇=a1或a2. 这样只需证明F＇=a1或a2→F=0.

假设ξ0是F＇-a1的m重零点. 由Rouche定理，这里存在m个序列{ξin}(i=1,2,…,m)在Dδ/2= {ξ:|ξ-ξ0|＜δ/2}使得Fn＇(ξin)=a1，那么

由于f和f＇分担{a1,a2}CM，推出f＇-a1只有单零点，这就是ξin≠ξjn(1≤i≠j≤m)，得到

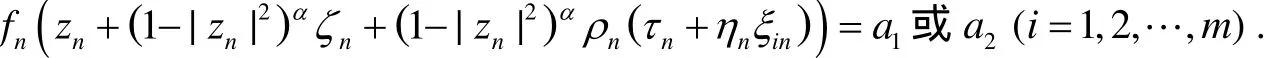
我们断言这里存在无穷多个n满足：

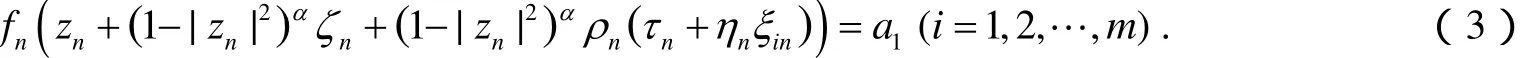
否则，假设对所有的n，存在j∈(1,…,m)满足：

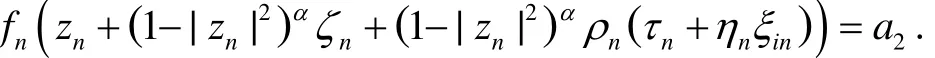
取一个固定数l∈(1,…,m)满足（对无穷多个n）：

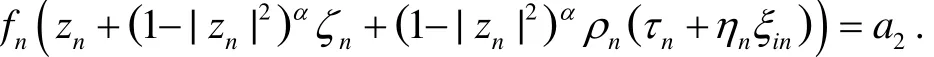
因而

这与F＇(ξ0)=a1矛盾，式（3）得证. 因而，Fn(ξin)=0(i=1,2,…,m)和ξin≠ξjn(1≤i≠j≤m). 当n→∞，我们有ξ0是F的零点且其零点重数至少为m. 这就证明了F＇=a1→F=0.

类似地，可以证明F＇=a2→F =0. 从而F=0⇔F＇=a1或a2得证.

由上述证明可知F＇-a1和F＇-a2只有单零点. 假设deg(F)=n，那么n=2(n-1)，则n=2. 令F=A(ξ-ξ1)(ξ-ξ2)，那么F＇=A(2ξ-ξ1-ξ2). 不失一般性，假设F＇(ξ1)=a1和F＇(ξ2)=a2，我们得到a1+a2=0. 这与条件矛盾. 因而定理2得证.

[1] SCHIFF J. Normal families[M]. New York: Springer, 1993.

[2] YANG Chunchung, YI Hongxun. The uniqueness theory of meromorphic functions[M]. New York: Kluwer Academic Publishers, 2003.

[3] SCHWICK W. Sharing values and normality[J]. Arch math (Basel), 1992, 59(1): 50-54.

[4] PANG Xuecheng, Zalcman L. Normal families and shared values[J]. Bull London Math Soc, 2000, 32(3): 325-331.

[5] LAPPAN P. A criterion for a meromorphic function to be normal[J]. Comm Math Helv, 1974, 49(1): 492-495.

[6] LEHTO O, Virtanen K I. Boundary behaviour and normal meromorphic functions[J]. Acta Math, 1957, 97(1): 47-65.

[7] 庞学诚. 亚纯函数的正规族与正规函数[J]. 数学年刊，2000, 21A(5): 601-604.

[8] FANG Mingliang, Zalcman L. Normality and shared sets[J]. J Aust Math Soc, 2009, 86(3): 339-354.

[9] 刘晓俊，庞学诚. 分担值与正规函数[J]. 数学学报，2007, 50(2): 409-412.

[10] LU Feng, XU Junfeng. Sharing set and normal families of entire functions and their derivatives[J]. Houston J Math, 2008, 34(4): 1213-1223.

[11] WULAN Hasi. On some classes of meromorphic functions[D]. Helsinki: Ann Acad Sci Fenn Mathematica, 1998.

[12] XU Yan. The α-normal functions[J]. Computers and Math Appl, 2002, 44: 357-363.

[13] XU Yan. Normal functions and α-normal functions[J]. Acta Mathematica Sinica (English Series), 2000, 16(3): 399-404.

The Normal Family and Sharing Set of Holomorphic Functions

XU Jun-feng
(School of Mathematics and Computation Science, Wuyi University, Jiangmen 529020, China)

In this paper, the idea of the sharing set was used to prove the following theorem: Let F be a family of holomorphic functions in the unit disc, a1and a2be two distinct finite numbers with a1+a2≠0. If α≥1, for any f∈F, Ef(S)=Ef＇(S ), S={a1,a2} in the unit disc, then f is an α-normal function.

holomorphic functions; meromorphic function; normal function; shared sets

O174.52

A

1006-7302（2011）01-0001-05

2010-07-27

国家自然科学基金资助项目（10771121）；广东省自然科学基金资助项目（9452902001003278）；广东省高校优秀青年创新人才培养项目（LYM08097）

徐俊峰（1979—），男，湖北南漳人，副教授，博士，研究方向为复分析及其应用.