GPS三频组合观测量的特征及应用研究①

吕志成，刘增军，王飞雪

（国防科学技术大学 电子科学与工程学院卫星导航研发中心，湖南 长沙410073）

0 引 言

GPS由美国国防部于1973年开始研发，经过20多年的研制和试验，于1995年初具备完全的工作能力［1]。经过几十年的不断发展，GPS作为新一代的卫星导航定位系统已在军事、交通运输、测量测绘、高精度时间比对以及资源勘探等诸多领域得到了广泛的应用。为了进一步巩固GPS在卫星导航领域的领先优势和提高系统服务质量，美国政府在1999年提出了GPS现代化计划，采取的措施包括在导航信号L2上增加第二个民用码（L2C）和增设第三个民用导航信号L5（1 176.45MHz）。通过使用所有三个频率信号（L1C／A，L2C和L5）的载波相位观测信息以及差分处理技术，可以快速获得高精度的解算结果。主要针对GPS三频观测值的组合形式、特征参数以及应用前景进行研究。

1 载波相位双差观测方程

GPS精密定位一般采用双差载波相位观测值作为原始观测数据，形成双差观测值的过程中可以极大削弱甚至消除许多空间相关及测站、卫星相关的系统误差，减少待估参数的个数，从而简化观测方程的表达形式。双差载波相位观测方程可以表示为

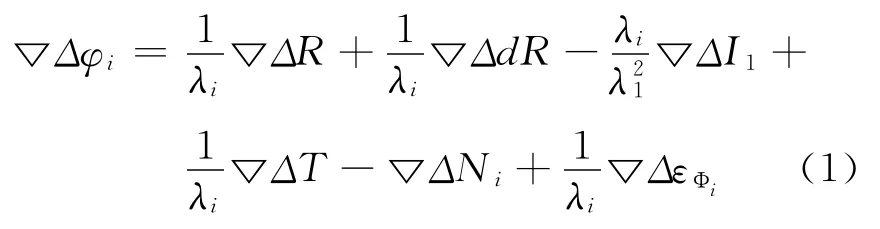
式中：▽Δ为双差算子；φi为第i个频率载波相位观测值，单位：周（i＝1，2，3）；λi为第i个频率载波波长，单位：m（i＝1，2，3）；R 为接收机与卫星间几何距离，单位：m；dR 为卫星轨道误差，单位：m；I1为L1频率上的电离层时延，单位：m；T为对流层时延，单位：m；Ni为第i个频率载波相位整周模糊度，单位：周；εΦi为第i个频率载波相位观测噪声（包括接收机噪声和多径等），单位：m.

由式（1）可以看到，双差观测值中消除了卫星钟差和接收机钟差的影响，残余的误差主要包括卫星轨道误差残差、电离层时延残差、对流层时延残差以及包括接收机噪声、多径效应等在内的观测噪声。多径误差和接收机噪声在时间和空间上均不具备明显的相关性，因此，无法通过差分方法进行有效的削弱和消除，在基线解算中通常在随机模型中进行考虑［2]。

2 载波相位观测值的线性组合

GPS现代化实现后，将成为拥有三个民用频率信号的多频卫星导航系统。多个频率信号的使用，使得载波相位观测值的线性组合形式更加多样，合理的选择线性组合方式和工作顺序，将有助于改善整周模糊度的解算成功率和效率［3]，提高粗差探测和周跳检测与修复的精度和有效性［4－5]。下面详细分析载波相位观测值的线性组合形式及其性能，为基线数据处理策略的制定提供参考依据。

2.1 线性组合的一般形式

三频载波相位观测量线性组合的一般表达式可写为

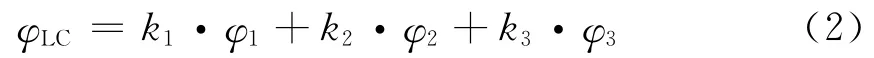
式中：φi（i＝1，2，3）表示第i个载波信号对应的相位观测值；ki（i＝1，2，3）为线性组合系数；φLC为线性组合后的载波相位观测量。φLC对应的整周模糊度NLC，可表示为

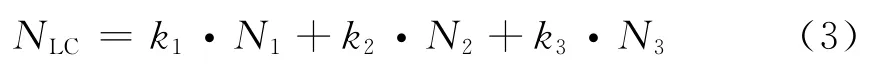
式中，Ni（i＝1，2，3）表示第i个载波信号对应的整周模糊度，为了保证NLC的整数特征，在实际应用中ki（i＝1，2，3）分别取为整数。

对于三频双差观测方程（见式（1）），其线性组合观测量可表示为

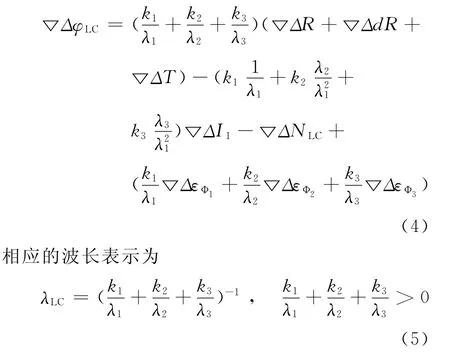
2.2 线性组合的误差分析

1）几何相关误差

根据式（4），双差观测值线性组合后几何相关误差可表示为

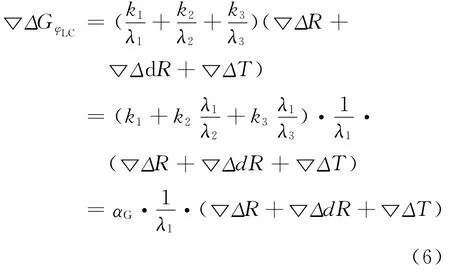
2）电离层误差

由式（4）可以看出，双差观测值线性组合后电离层误差为

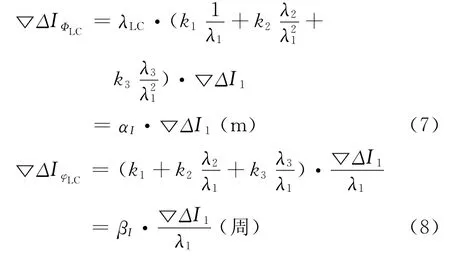
3）测量噪声

为了简化分析，假设不同频率上的载波相位观测误差相互独立，以米为单位的测量噪声均方差等于相应波长的α倍，即σi＝λi·α，则根据误差传播定律，双差观测量的观测噪声为

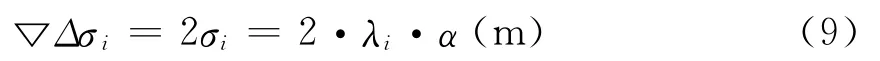
线性组合观测量的观测噪声表示为

2.3 电离层无关线性组合及性能分析

电离层误差及其残差是影响基线解算质量的重要因素之一，而电离层无关线性组合可以消除电离层误差的影响，为整周模糊度的快速、正确搜索提供了可能。电离层无关线性组合在实际应用中具有重要的意义。下面详细讨论电离层无关线性组合的形式及性能。

根据上述对载波相位观测值线性组合误差的分析，电离层无关线性组合应满足以下条件

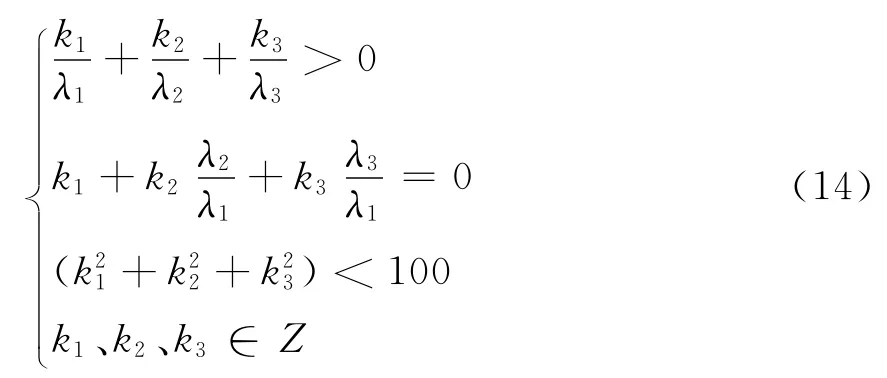
上述方程组属于含不等式约束条件的非满秩方程组。考虑到λ1＜λ2＜λ3，现令k2、k3∈Z，k1∈R且限定取值范围k2＝ ［－10，10]，k3＝ ［－10，10]，得到k1的一组浮点解序列，将k1取整得到其定点解序列「k1」，符号「·」表示对浮点解进行四舍五入运算。理论上，浮点解与定点解的偏差越小，则组合后观测量包含的电离层误差越小，偏差最小的五组线性组合及其特征值列于表1。

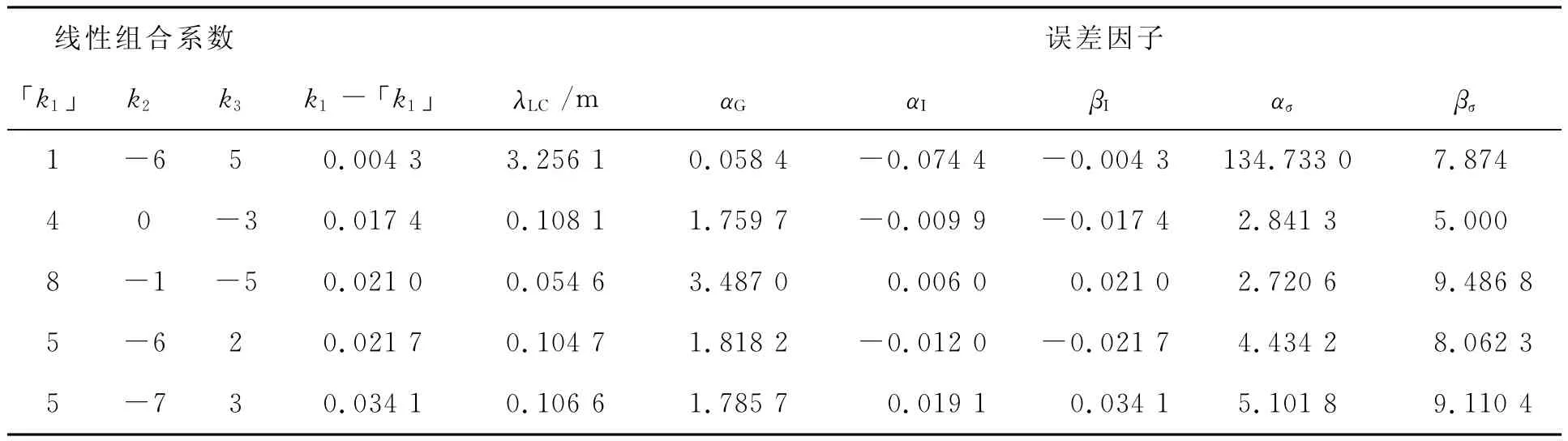
表1 满足电离层无关条件的部分候选组合及其特征值

从表1中可以看到，上述各线性组合除（1，－6，5）外，组合后的波长均小于任意载波波长，较小的波长将对整周模糊度的解算产生不利影响。组合观测值的电离层误差（αI和βI）与载波L1相比降低1～2个数量级，在基线解算中可以忽略不计。与载波L1相比，组合观测值的观测噪声（ασ和βσ）放大数倍，同时几何相关误差（αG）也有不同程度的增加。线性组合（1，－6，5）在波长和电离层误差方面较其他组合具有明显的优势，但以m为单位的观测噪声被放大2个数量级。在实际应用中，需要综合考虑原始观测数据的质量、解算目标和使用的算法等因素，合理选择线性组合形式。

2.4 几种特殊的线性组合及性能分析

根据前面的介绍，通过将多个频率观测量进行合理的线性组合，可以构造出许多具有长波长、低噪声等良好特征的组合观测量，有助于提高整周模糊度解算的成功率和定位精度。选择不同的系数（k1，k2，k3），可以得到一系列具有不同特性的组合观测量，其中比较重要的有超宽巷组合（EWL）、宽巷组合（WL）、中巷组合（ML）和窄巷组合（NL），详细的参数列于表2。从表2中可以看到，超宽巷组合波长最长（586.1cm），具有较小的以周为单位的测量噪声、几何相关误差以及电离层时延误差，这些特性对于整周模糊度的解算极为有利，但是超宽巷组合观测量以m为单位的测量噪声较大，一般不宜直接应用于精密定位计算；宽巷组合和中巷组合波长分别为86.2cm和75.1cm，具有适中的电离层误差和测量噪声，有利于整周模糊度的确定，同时与超宽巷组合相比，以m为单位的测量噪声显著降低，可以提供更精确的定位结果；窄巷组合的波长仅为10.7cm，且几何相关误差和电离层误差较大，不利于整周模糊度的确定，但较小的观测噪声使其在精密定位解算方面具有明显的优势；（1，0，0）组合相当于载波 L1单频观测，通常使用载波L1观测量可以得到较好的解算结果，在实际应用中载波L1的整周模糊度往往也是最关心的参数之一。

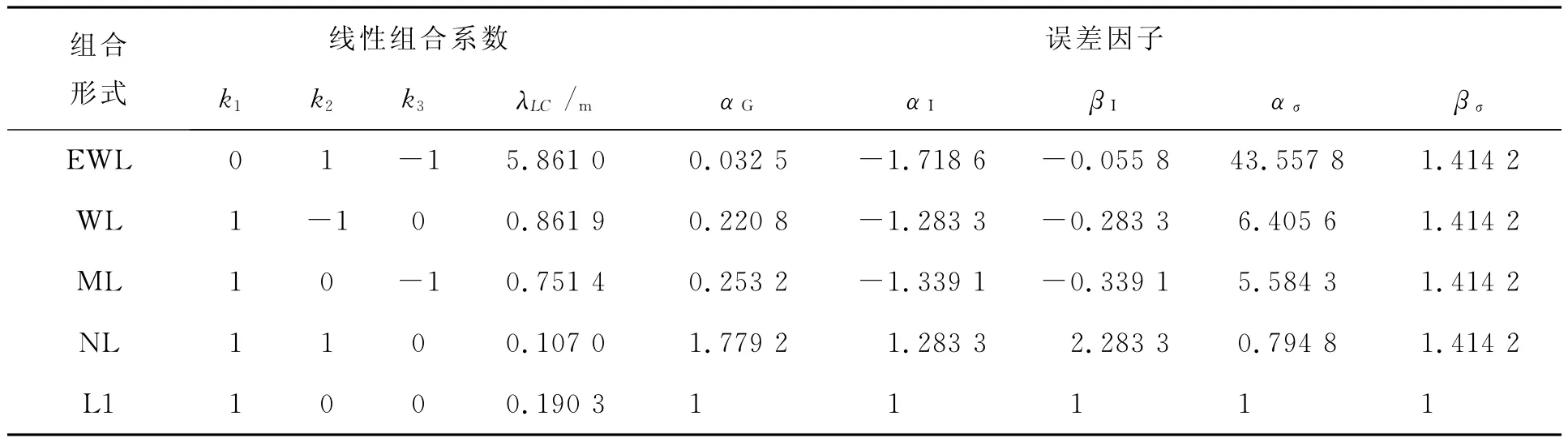
表2 几种特殊线性组合及其特征值

分析线性组合序列EWL／WL／ML的特征值的变化可以看到：序贯组合观测值的波长由5.86 m依次递减直0.75m，以m为单位的测量噪声放大系数由43.56依次递减至5.58，而以周为单位的测量噪声放大系数则保持不变，电离层时延误差虽然有所增加但幅度有限，这说明采用上述序贯序列组合，在测量噪声水平一定的条件下，可以逐步提高模糊度解算的成功率和基线解算的精度。

3 线性组合在解算中的应用

GPS现代化的实施，使民用信号的数量和质量得到了不同程度的提高，将不同频率观测量进行合理组合可以得到许多具有低噪声、长波长、电离层无关和几何无关等良好特性的组合观测量，为提高整周模糊度搜索效率和基线解算质量创造了有利条件。如：在电离层误差修正方面，以前的单频和双频系统只能通过模型或差分方法消除一阶电离层时延的影响，误差改正精度有限，三频观测数据的组合应用可以将电离层时延消除至高阶项，有效分离电离层误差与对流层误差、多径效应等的影响［6]。借助三频组合观测量的优良特性，可以将观测数据中的粗差和周跳进行放大，更好地进行检测和修正，提高观测数据质量［4]。在整周模糊度解算过程中，还可以充分利用不同组合观测量各自的特点，在不同的解算阶段采用不同的组合形式，进一步提高模糊度搜索的效率和成功率，使GPS在长基线和高动态实时等应用领域的应用成为可能，类似的方法有 TCAR、CIR、MCAR［7－10]等。

4 结 论

随着GPS现代化的逐步实现，对于三频观测量的组合形式及其特性的研究逐渐成为GPS应用领域的研究热点。将多频观测数据进行合理的组合可以得到许多具有良好特性的组合观测量，如低噪声、长波长、电离层无关和几何无关等，这些特征对于特定的应用环境和系统具有重要的意义，可以有效提高电离层误差改正、周跳检测与修正、整周模糊度解算、精密定位等作业质量，使GPS在长基线解算、高动态实时定位以及RTK测量领域的应用成为可能。

［1]寇艳宏.GPS原理与应用［M].2版.北京：电子工业出版社，2008.

［2]SATIRAPOD C，WANG Jin－ling，RIZOS C.Simplified MINQUE procedures for the estimation of variance－covariances components of GPS observables［J].Surv.Review，2002，36（286）：582－590.

［3]范建军.GNSS三频精密测量定位系统的数据处理理论及方法研究［D].长沙：国防科学技术大学，2007.

［4]王贵文.基于三差观测量的实时动态GPS周跳修复方法研究［J].武汉大学学报，2007，32（8）：711－714.

［5]刘旭春.GPS三频数据在周跳和粗差探测与修复中的应用［J].煤炭学报，2006，31（5）：585－588.

［6]伍 岳.GPS现代化后电离层折射误差高阶项的三频改正方法［J].武汉大学学报，2005，30（7）：601－603.

［7]FORSSELL B，MARTIN NEIRA M，HARRIS R A，et al.Carrier phase ambiguity resolution in GNSS－2［C]／／Proceeding of ION GPS－97，Kansas ，USA，1997：1727－1736.

［8]JUNG J，ENGE P，PERVAN B.Optimization of cascade integer resolution with three civil GPS frequencies［C]／／Proceeding of the ION GPS－00，Salt Lake City，2000：2191－2201.

［9]JUNG J.High integrity carrier phase navigation for future LAAS using multiple civilian GPS signals［C]／／Proceding of ION GPS－99，Nashville，1999：727－736.

［10]WOLFGANG W，JON W.TCAR and MCAR options with Galileo and GPS［C]／／Proceeding of the ION GPS／GNSS－03，Portland，2003.