GDP的时间序列模型的建立及应用——以 兰 州 市 为 例

金鑫 王蕾 高峰 张恒

(兰州交通大学数理与软件工程学院，甘肃 兰州 730070)

GDP的时间序列模型的建立及应用
——以 兰 州 市 为 例

金鑫 王蕾 高峰 张恒

(兰州交通大学数理与软件工程学院，甘肃 兰州 730070)

GDP是人们了解和把握一个国家或地区宏观经济运行状况的有效途径。文章在介绍时间序列的基础上，利用Eviews统计软件及非参数统计方法，对兰州市1978—2010年的GDP数据进行实证分析，建立了ARIMA(1，1，4)模型。检验表明，该模型具有较好的预测效果，利用该模型对兰州市未来5年的GDP进行了预测。

GDP;时间序列分析;ARIMA模型;非参数统计方法;预测

0 引言

GDP是衡量一个地区经济实力的一项重要指标，它不仅考虑了经济总量的大小，而且结合了人口多少的因素。因此，准确预测兰州市的GDP对兰州市经济的发展具有重大参考价值，与此同时一些国内外专家学者对GDP的发展规律及预测方法进行了许多研究。GDP的普通预测方法是利用现有的GDP和现在经济增长率来计算若干年以后的GDP，这种方法没有考虑经济波动的影响和随机因素的干扰，预测结果将会出现较大的偏差。文献[1]以我国1954—2004年的 GDP数据为依据，采用BOX-Jenkins方法建立ARIMA(1，1，1)模型，揭示我国GDP增长变化的规律性，并对回归结果进行实证分析。文献[2]利用Eviews3.1统计软件对1950—2004年广西的GDP进行了分析，建立了 ARIMA(1，1，2)模型，而且模型引入了回归项——全社会固定资产投资额，对广西国内生产总值作出预测。以上文章在模型定阶时都是根据ACF图(自相关函数图)及PACF(偏自相关函数图)来判断模型的阶数，如果图形的拖尾和截尾特征不明显，阶数的判断容易出现错误，因此所得模型不一定是最佳模型。本文对最佳阶数的确定则是在AIC准则下进行重复拟合得到的，而且在模型的适应性检验时利用非参数统计方法进行检验比上述文章更客观。

改革开放以来，兰州市经济社会发展取得了辉煌的成就。2007年GDP达到732.76亿元，是改革之初1978的33.6倍，由图1可以看出，城市经济是在波动中发展前进的，GDP的增长呈现阶段性的成长过程，经济发展经历了3次大的起伏周期。

1978—1991年是改革开放后经历的第一个发展周期，年均增长6.6%，1984年达到最高点，然后不断回落，1991年达到2.2%的低点。其特点是波动幅度大，增长率变化不平稳。

第二个周期始于90年代初期1992年，到1994年达到最高点，然后逐渐减速，1999年达到最低点，2000年结束，这一周期平均增长速度达到了9.6%。其特点为波动幅度相对较小，增长率变化呈现出一定规律。

第三个周期始于2001年，经济发展速度不断加快，表现出稳定加速的特征，目前仍处于该发展周期，平均增速为11.42%。特点为高位增长，变化平稳。

从周期波动幅度来看，兰州市经济波动呈现出逐步减缓的趋势。在1978—1991年的经济增长周期中，GDP增长的最大幅度为17%(1984年)，而最小值为 -3.3%(1981年)，其离差即波动幅度为20.3%。在第二个周期中最大波动幅度12.6%与最小值8.0%的差为4.6，这8年间增长最大波动仅为4.6%，相比较第一个周期波动幅度下降了将近4倍。在统计学中，平均值反映的是随机变量的集中趋势，而标准差则反映了变量的离散程度。这3个周期平均增长率不断加速上升，但标准差却不断减小，分别为 5.45、1.48、1.45，这说明经济增长速度不断加快，而波动幅度却不断减小，经济发展更趋稳定。

1ARIMA模型介绍

对于一个非平稳时间序列来说，方差、均值和协方差等都是随时间变化的，也可以说，非平稳时间序列在各时间段上的随机规律是不同的，很难通过时间序列已知的信息去掌握序列整体上的随机性。1970年，BOX和Jenkins提出了以随机理论为基础的时间序列分析方法:自回归(AR)模型，移动平均(MA)模型以及自回归求积移动平均(ARIMA)模型。AR模型和 MA模型就是ARIMA模型的特例。若对一个有明显趋势的非平稳时间序列，利用d阶差分之后可变为平稳的时间序列，则可建立ARIMA(p，d，q)模型。

1.1 ARIMA(p，d，q)模型的一般形式

Φ(B)▽dxt=Θ(B)εt，E(εt)=0，Var(εt)=，E(εtεs)=0，s≠t Exsεt=0，∀s ＜ t。其中，▽d=(1-B)d;Φ(B)=1-φ1B-…-φpBp为平稳可逆ARIMA模型的自回归系数多项式;Θ(B)=1-θ1B-…-θqBq为平稳可逆ARLMA模型的移动平滑系数多项式。

1.2 ARIMA(p，d，q)模型的建模思想

1)根据时间序列的自相关函数(ACF)图和偏自相关函数(PACF)图，ADF单位根检验观察其方差及季节性变化规律，识别该序列的平稳性。

2)数据进行平稳化处理，如果数据序列是非平稳的，有增长或下降趋势等，则要对数据进行差分处理。

3)如果时间序列的偏自相关函数是截尾的，而自相关函数是拖尾的，则可判断此序列适合AR模型;如果平稳时间序列的偏自相关函数是拖尾的，而自相关函数是截尾的，则此序列适合MA模型;如果平稳时间序列的偏自相关函数和自相关函数都是拖尾的，则适合ARMA模型。

4)进行参数估计。

5)进行假设检验，诊断白噪声序列。

1.3 模型定阶

1)Ljung-Box(1978)检验。

2)利用ACF图和PACF图的性质来确定模型的阶数。

3)最佳准则函数定阶法，即Akaike提出的AIC准则。该准则是在模型参数极大似然估计的基础上，对模型的阶数和相应参数同时给出一组最佳估计，选取使AIC达到最小的一组阶数为理想阶数。

2 数据分析及预测

2.1 模型的识别和定阶

兰州市国内生产总值时间序列数据(1978—2010)见表1。兰州市GDP用Y表示，年份用X表示，X和Y的变化曲线见图1。

表1 1978—2010年兰州市GDP

图1 X和Y的变化曲线图

由图1可以看出，随着改革开放和人民生活水平的提高，兰州市的GDP总体上出现不断增长的趋势，具体来说是一种指数增长趋势，非水平平稳。

对于指数增长的非平稳时间序列，一般方法是通过对指数增长趋势进行对数变换后转换为线性趋势，然后再对其进行差分来消除线性趋势。所以可对兰州市GDP数据取对数并作一阶差分后得到时间序列图，如图2所示。

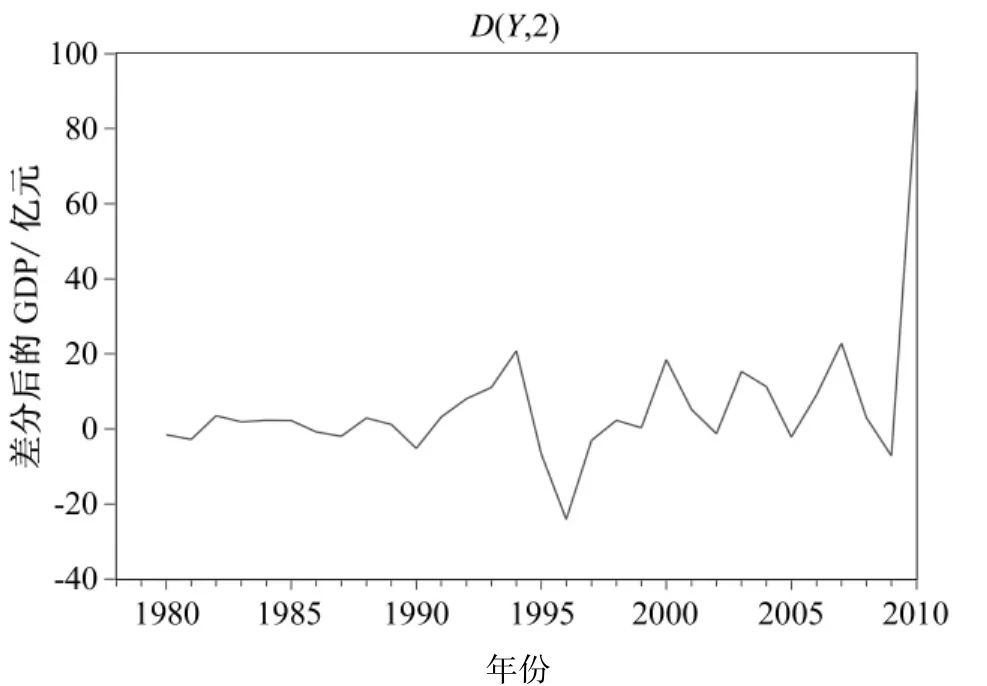
图2 差分后的时间序列图

由图2可以看出，取对数并作一阶差分后，时间序列基本平稳。因此，可利用取对数变换和一阶差分后的数据进行模型的识别和定阶，所以可以确定ARIMA(p，d，q)模型中的d应为1。为了确定模型中的p和q，作出一阶差分后的自相关(ACF)图和偏自相关(PACF)图，分别见图3、图4。为了能找到最佳的阶数，采用最佳准则函数定阶法中的Akaike最小信息准则(AIC)来判定模型的最佳阶数。原序列的相关图和偏相关图如图3所示。

图3 原序列的相关图和偏相关图

由图3可以看出，原序列是一个非平稳时间序列。

对原序列取对数后的相关图和偏相关图如图4所示。

图4 取对数后的相关图和偏相关图

由偏相关图可以看出，在k=2后呈截尾特征。由此判定应用AR(1)模型拟合取对数后的序列数据。共选择2个AR(2)，一个含有位移项，另一个不含。另外考虑相关图k=4时有峰值，随后按照正弦衰减，所以建立一个 ARIMA(1，1，4)模型或 ARIMA(2，1，4)模型。

2.2 模型的建立

利用Eviews软体分别作出ARIMA(2，1，4)和 ARIMA(1，1，4)模型的参数，如图 5、图 6所示。

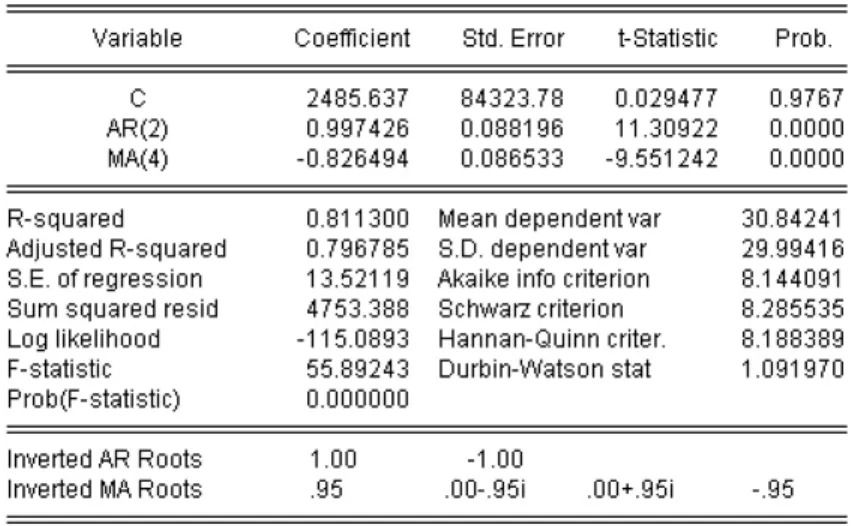
图 5 ARIMA(2，1，4)模型参数

图 6 ARIMA(1，1，4)模型参数

由图5可以看出，ARIMA(2，1，4)模型的AIC值为8.144 091，由图6可以看出，ARIMA(1，1，4)模型的 AIC 值为7.247 343，所以本文采用ARIMA(1，1，4)模型来预测兰州市的GDP。

2.3 模型的检验

模型的检验也就是对所建模型的优劣性进行检验，通过对原序列数据与拟合数据的误差(残差)序列进行检验来实现。若残差序列为白噪声序列，模型应用于预测是合理的;若残差序列不是白噪声序列，说明模型应用于预测是不合理的。对模型拟合后的残差序列用Eviews处理后得出的不同延期数QLB统计量为:Q(6)=47.437，Q(12)=49.630，Q(16)=50.340，括号内数字为对应检验统计量的P值。由此可知，在检验的显著水平为0.05的条件下，由于延迟6阶的卡方检验统计量P≫0.05，所以该差分序列是白噪声序列，即拟合后的残差序列没有信息可用，这个序列值的变动是随机波动的。

为了验证有效性给出了实际值与预测值得对比图，如图7所示。

图7 实际值与预测值对比图

由图7可以看出拟合效果很好，没有出现太大的偏差，说明模型是有效的。

2.4 模型的预测

由 ARIMA(1，1，4)模型:

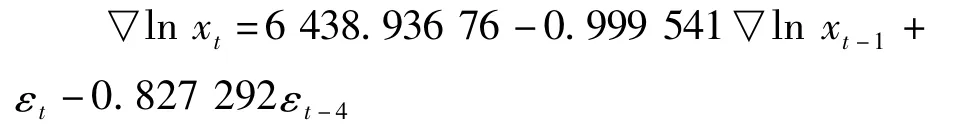
又因为:▽ln xt=ln xt- ln xt-1

可得ln xt的预测公式为:

所以可得序列X的预测公式:

通过上述讨论可知，用ARIMA(1，1，4)可很好地预测兰州市2011—2015年的 GDP，见表3(此模型只能用于中短期预测)。

表3 2011—2015年兰州市GDP预测数

3 结语

通过对兰州市1978—2010年间的GDP时间序列进行分析，建立 ARIMA(1，1，4)模型，借助模型参数对原序列进行量化表示，最终使拟合的残差序列成为白噪声序列，拟合的结果在理论上具有说服力，在应用上切实可行。但根据ARIMA时间序列模型方法得到的兰州市GDP预测结果，应该说是个预测值，而且只能是中短期预测。

[1]杨叔子，吴雅，轩建平.时间序列分析的工程应用[M].武汉:华中科技大学出版社，2007.

[2]吴鉴洪.时间序列中回归模型的诊断检验[D].上海:华东师范大学，2007.

[3]Peter J Brockwell，Richard A Davis.Time Series and Theory Methods[M/OL].2nd ed.[2011 - 03 - 03].http://www.ebookee.net/Time-Series-Theory-and-Methods-Second-Edition _1091134.

[4]潘红宇.时间序列分析[M].北京:对外经济贸易大学出版社，2006.

[5]Sudhakar M Pandit[美]，Shien-Ming Wu.Time Series and System Analysis with Applications[M].New York:Wiley，1983.

[6]冯兰刚，郭宏，都沁军.基于ARIMA模型的河北省城市化发展研究[J].商业时代.2008，26(25):103 -104.

[7]樊亮，常迎香，李菊梅.时间序列分析模型在甘肃省GDP中的应用[J].甘肃科学学报，2009，21(4):140 -142.

[8]李菊梅，袁杰，樊亮.甘肃省全社会固定资产投资的ARIMA模型预测[J].经济研究刊，2009，28(66):7 -8.

[9]李菊梅，樊亮，崔俊峰.用时间序列分析方法预测我国的进出口总额[J].重庆工学院学报:自然科学版，2008，22(12):136-138.

Time Series Model Constitution and Application of GDP——A Case Study of Lanzhou

JIN Xin WANG LeiGAO Feng ZHANG Hen

(School of Mathematics，Physics and Software Engineering，Lanzhou Jiaotong University，Lanzhou 730070)

GDP is an efficient tool for people to know and hold macroscopically economics status of a country or area.Based on the introduction time series model，this paper gives an empirical analysis of the GDP data(1978—2010)of Lanzhou，by using Eviews ststistical software and nonparametric method in statistics.Based on this，the ARIMA(1，1，4)time series model is established，whose examination results indicate that it has a better forecast effect.And then，this paper uses it to forecast the GDP of Lanzhou in the next five years.

GDP;time series analysis;ARIMA model;non-parametric method in statistics;forecast

F127;O212.1

A

1671-0436(2011)03/04-0067-05

2011-07-08

金鑫(1982— )，男，硕士研究生。

责任编辑:张秀兰