一种带兴趣度的正负关联规则挖掘算法

王 璇

(福建对外经济贸易职业技术学院信息技术系，福建 福州 350016)

一种带兴趣度的正负关联规则挖掘算法

王 璇

(福建对外经济贸易职业技术学院信息技术系，福建 福州 350016)

针对负关联规则挖掘所带来的问题，提出加入最大支持度来控制频繁项集生成规模，改进了相关性的计算公式，并将其用作正负关联规则的兴趣度来剔除无兴趣的关联规则，限制关联规则中的前后件项目个数来保证挖掘出的关联规则的实用性和可理解性。最后，给出一种能够同时挖掘正负关联规则的算法，实验结果表明算法是有效的、可行的。

正负关联规则;最大支持度;兴趣度;相关性

0 引言

关联规则挖掘最早由Agrawal等人在文献[1]中提出，它用形如A⇒B的蕴含式来表示项集A的出现带动项集B的出现，从而揭示了数据之间有意义的关联。关联规则自提出以来得到深入的研究，并广泛应用于商业、金融、电信等行业。但是，传统形式的关联规则只能挖掘出数据之间正面的关联，而无法发现数据间的负关联，即项集A的出现会降低项集B的出现或使B不出现。在实际应用中，尤其是在投资分析和竞争分析等许多领域，负关联规则与正关联规则一起为正确决策提供更加全面的信息，其作用是不可低估的。

相比正关联规则，人们对负关联规则的研究起步较晚。1997年，文献[2]中首次提到了2个频繁项集间的负关联问题;文献[3]研究了强负关联规则问题;文献[4]对负关联规则进行了形式定义;文献[5]引入相关性度量来区别不同形式的正负关联规则，避免挖掘出互相矛盾的关联规则;文献[6]通过引入过频繁项集解决负关联规则中的频繁项集爆炸问题。研究表明，引入负关联规则后，生成的频繁项集数量将迅速增长，同时也出现了更多无用及矛盾的规则。本文通过引入最大支持度及最小兴趣度等约束条件，有效地控制了负关联规则挖掘中频繁项集数量的过快增长，并进一步约束生成的关联规则，较好地解决了以上问题。

1 相关知识

1.1 负关联规则的定义

设 I={i1，i2，…，in}是 n个不同项目的集合，D={T1，T2…，Tm}为事务数据库，其中事务 Tj⊆I(1≤j≤m)。一条负关联规则就是一个形如A⇒﹁ B(或﹁ A⇒B，﹁ A⇒﹁ B)的蕴涵式[4]，其中，A，B⊆T，A∩B=∅，且满足 sup(A⇒﹁ B)≥min_sup，conf(A⇒﹁ B)≥min_conf。

对于一条支持度为sup，置信度为conf的负关联规则A⇒﹁B，表示在事务数据库D中有(100×sup)%的事务包含A但不包含B，包含A的事务中有(100×conf)%的事务不包含B。负关联规则揭示了事务之间互相排斥的一种关系，具有十分重要的现实意义。

限于篇幅，仅讨论A⇒﹁B型的负关联规则挖掘问题，其思想亦适合于﹁A⇒B型的负关联规则。另外，﹁A⇒﹁B型的负关联规则挖掘比较简单，实际应用不多，因此不再讨论。

1.2 负关联规则的支持度、置信度计算

与正关联规则挖掘相同，要生成包含负项目的频繁项集，需要计算每个负项集的支持度。由于负项目表示不发生的项集，直接计算其支持度比较困难。文献[5]中提出了一种利用相应正项集的支持度导出负项集支持度的方法，即负关联规则AB的支持度计算公式为:

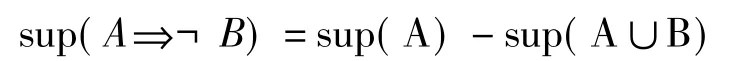
同理可得置信度计算公式，即:

2 负关联规则挖掘中的问题及解决方法

2.1 过频繁项集与最大支持度

在传统的关联规则挖掘中，对频繁项集剪枝的策略是根据频繁项集的Apriori性质，即一个频繁项集的所有非空子集都必须是频繁的，反之，任意非频繁项集的所有超集也一定是非频繁的。对于一般的数据集，大多数项集的支持度都不高，因此，在频繁项集生成过程中，使用最小支持度对候选项集的重要程度进行评估，如果某个项集支持度小于最小支持度阈值，则其所有超集也是非频繁的，因而可以对该项集及所有超集进行剪枝，从而有效地减少计算量。相比于正关联规则挖掘，在负关联规则挖掘中，高支持度的负项集非常普遍，因为其对应的正项目的支持度若为sup(i)，则该负项目的支持度sup(﹁i)=1-sup(i)≈1。因此，在负关联规则挖掘中，仅仅依靠最小支持度来对项集剪枝，效果并不理想，无法控制频繁项集的指数级增长。

为此，本文引入最大支持度，对支持度大于最大支持度的包含负项目的项集称为过频繁项集，参照文献[6]给出其定义:

定义1设能产生有兴趣的关联规则项集的最大支持度为max_sup，项集X为包含负项目的项集，如果sup(X)＞max_sup，则称X为过频繁项集。

文献[6]中还证明了过频繁项集的一个性质:

性质1过频繁项集及其所有超集不可能产生有兴趣的关联规则。

反之，对于满足最大支持度阈值的项集A，即对sup(A)≤max_sup，容易证明以下性质:

性质2设项集A满足最大支持度阈值，则其所有超集也满足最大支持度阈值。

证明设项集B⊃A，则有sup(B)≤sup(A)。已知sup(A)≤max_sup，故有sup(B)≤sup(A)≤max_sup，命题得证。

由性质1和性质2可知，对项集最大支持度的计算只要在生成频繁1-项集时剔除支持度大于最大支持度的项集，即可保证后面的频繁k-项集(k≥2)都满足最大支持度阈值。因此，在频繁项集生成过程中，结合最大支持度和最小支持度的阈值限制，对项集进行剪枝，可以有效地控制频繁项集的生成规模。

2.2 关联规则的相关性

许多研究表明，基于传统的支持度—置信度评价框架生成的关联规则很多是无意义的，甚至是矛盾的，主要原因之一是支持度—置信度框架无法对规则前后件之间的关联程度作更深入的评价。Brin等人在文献[7]中提出了相关性的概念，用于判断规则前后件的相关程度，具体定义如下:

corrA，B的取值范围是[0，∞)，具体的取值有3种关系:

①corrA，B＞1，此时 A和 B为正相关，表示二者相互提升了对方出现的可能性，值越大则关联程度越高;

②corrA，B=1，此时A和B相互独立，表示二者的出现与对方无关;

③corrA，B＜1，此时 A和 B为负相关，表示二者相互降低了对方出现的可能性，值越小则负关联程度越高。

早期的研究只保留了相关性大于1的规则，即正关联规则，而其他情况只进行简单的删除。文献[5]中使用相关性概念来区分正负关联规则，并证明了当corrA，B＞1时，产生A⇒B型规则;则有:

当 corrA，B＜1 时，产生 A⇒﹁ B 型规则;当 corrA，B=1时，不生成关联规则。

2.3 相关性的改造

文献[8]中对相关性进行了修正，将其用作正负关联规则的兴趣度，但是依然没有克服相关性取值的缺陷，即其取值没有上限，且在值1两侧不对称，这将不便于用户设置统一的门槛值。本文在文献[8]的基础上对相关性加以进一步的改造，将其值域映射到[-1，1]区间内，从而作为正负关联规则评价的一个新的兴趣度，定义如下:

定义3对一条候选关联规则A⇒B，其兴趣度为:

假设λ =sup(B)为常数(0 ＜λ ＜1)，intrA，B可改写为:

由图1 可以看出，intrA，B∈(0，1]时，A 和B 正相关，此时产生 A⇒B 型规则;intrA，B∈(0，-1]时，A和 B负相关，此时产生 A⇒﹁B型规则;intrA，B=0时，A和B互相独立，不生成规则。具体计算时可将式(1)展开，即:

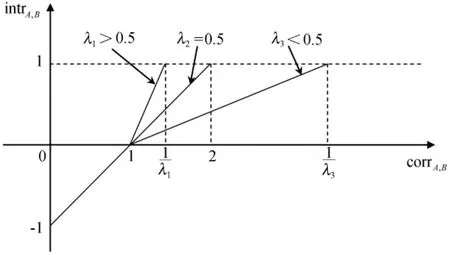
图 1 intrA，B与 corrA，B的关系

由于有最小/最大支持度的限制，sup(A)和sup(B)的值域为(0，1)，因此 intrA，B的取值范围为(-1，1)。在正负项目一起进行挖掘时，为方便设置统一的门槛值，可将intrA，B＜0的情况映射到(0，1)的区域，即|intrA，B|≥min_intr，而不必再分别对正、负关联规则设置不同的兴趣度阈值。

3 算法描述

虽然引入最大支持度从一定程度上控制了包含负项目的频繁项集的规模，以及加入兴趣度阈值来进一步约束生成的关联规则，但是仍然会生成大量的关联规则，尤其当数据集中包含的项目比较多时。实际上，若一条关联规则所包含的项目个数越多，该规则的可理解性就越差，所具有的实用价值往往也越低。因此，还要对关联规则的前后件项目个数进行限制，以保证挖掘出来的关联规则的实用性和可理解性。

包含正负项目的关联规则挖掘可以分解为2个子问题:①求出事务数据库D中的所有正负项目的频繁项集L;②从频繁项集L中生成满足约束条件的所有正负关联规则。对第1个子问题已有多个现成的算法可以借鉴，如 Apriori、FP-growth等，本算法基于FP树，采用含正负项目的FP 树构造算法Con_FPN_tree[9]。因此，第2个子问题是算法的核心问题。

算法:带兴趣度的正负关联规则挖掘算法IPNARM。

输入:事务数据库D，最小支持度 min_sup，最大支持度max_sup，最小置信度min_conf，最小兴趣度min_intr，前件包含最大项目个数max_former，后件包含最大项目个数max_back。

输出:正关联规则PRS，负关联规则NRS。

①扫描数据库D，根据最小支持度min_sup和最大支持度max_sup得到满足条件的频繁1-项集，调用Con_FPN_tree算法，得到包含正负项目的FPN_tree，再从FPN_tree中挖掘出频繁项集L;

②PRS=∅，NRS=∅;

③for each li∈L

IPNARM算法的基本思想:①在[min_sup，max_sup]阈值范围内，从FPN_tree中挖掘出所有包含正负项目的频繁项集L。②在L中逐一考查关联规则前件A和后件B，如果满足前后件项目个数的要求，则计算规则的兴趣度，判断生成关联规则的类型，转③，否则执行②。③若兴趣度满足最小兴趣度阈值且置信度大等于最小置信度，则输出相应的关联规则，否则转②，直到挖掘完所有的关联规则。

4 实验及结果分析

4.1 实验设计

为了对比验证本文算法的性能，在CPU为AMD Athlon 2.01 GHz，内存 1 GB，操作系统为Windows XP的环境下，用Visual C++6.0分别实现了IPNARM算法、PAR＆NAR_on_P-S_measure算法[8](简称PAR ＆NAR 算法)和文献[6]中的算法2(简称算法2)。采用的实验数据集来源于http://www.ics.uci.edu/～ mlearn/MLRepository.html上所提供的蘑菇数据库(Mushroom Database)，该数据库有8 124条记录，事务的平均长度为23，包含120个项目。

IPNARM算法所使用的参数为:max_sup=0.95，min_conf=0.5，min_intr=0.5，max_former=2，max_back=2。PAR＆NAR算法使用的参数为:min_conf=0.5，min_intr=0.5;算法 2 使用的参数为:max_sup=0.95，Nmax_neg=2。分别对3种算法挖掘的正负关联规则数量和运行时间进行对比实验。

4.2 结果分析

实验结果如图2、图3所示。

图2 3种算法挖掘出的关联规则数量

图3 3种算法的执行时间

5 结语

针对负关联规则挖掘所带来的问题，提出加入最大支持度来控制频繁项集生成规模，改进了相关性的计算公式，并将其用作正负关联规则的兴趣度来剔除无兴趣的关联规则，限制关联规则中的前后件项目个数来保证挖掘出来的关联规则的实用性和可理解性。提出一种能够同时挖掘正负关联规则的算法IPNARM，通过对比实验表明算法是有效可行的，尤其是当数据集中所包含的项目个数比较多时，能够保证关联规则挖掘的顺利进行。

[1]Agrawal R，Imielinaki T，Swami A.Mining Association Rules Between Sets of Items in Large Databases[C]//Washington.D C:Proc of the ACM SIGMOD Conference on Management of Data，1993:207 -216.

[2]Brin S，Motwani R，Silverstein C.Beyond Market:Generalizing Association Rules to Correlations[C]//Processing of the ACM SIGMOD Conference 1997.New York:ACM Press，1997:265 -276.

[3]Savasere A，Omiecinski E，Navathe S.Mining for Strong Negative Associations in a Large Database of Customer Transactions[C]//Proceedings of the IEEE 14th Intl Conference on Data Engineering.Los Alamitos:IEEE - CS，1998:494 -502.

[4]WU Xindong，ZHANG Chengqi，ZHANG Shichao.Mining Both Positive and Negative Association Rules[C]//Proceedings of the 19th International Conference on Machine Learning(ICML- 2002).San Francisco:Morgan Kaufmann Publishers，2002:658-665.

[5]董祥军，王淑静，宋瀚涛，等.负关联规则的研究[J].北京理工大学学报，2004，24(11):978 -981.

[6]马占欣，陆玉昌.负关联规则挖掘中的频繁项集爆炸问题[J].清华大学学报:自然科学版，2007，47(7):1212 -1215.

[7]Brin S，Motwani R，Silverstein C.Beyond market:Generalizing Association Rules to Correlations[C]//Processing of the ACM SIGMOD Conference 1997.New York:ACM Press，1997:265 -276.

[8]董祥军，宋瀚涛，姜合，等.基于最小兴趣度的正、负关联规则挖掘[J].计算机工程与应用，2004，27(12):24 -26.

[9]张玉芳，彭燕，刘君，等.一种含负项目的一般化关联规则挖掘算法[J].计算机工程与设计，2006，27(20):3904 -3908.

Algorithm with Interest Measure for Mining Positive and Negative Association Rules

WANG Xuan

(Depatrment of Information Technology，Fujian International Business Economic College，Fuzhou 350016)

In terms of the negative association rules mining problems，maximum support is proposed to be used to control the growth of the frequent itemsets.The formula of correlation is improved and used as an interest measure for the positive and negative association rules to get rid of the uninterested rules.The former and back association rules are limited to ensure the practicability and comprehensibility of the association rules.At last，this paper gives the algorithm which can simultaneously mine positive and negative association rules.And the experimental results show that this algorithm is efficient and feasible.

positive and negative association rules;maximum support;interest measure;correlation

TP311.13

A

1671-0436(2011)03/04-0016-05

2011-05-19

王璇(1978— )，女，讲师。

责任编辑:唐海燕