船舶传动装置多体动力学和有限元仿真技术

马炳杰，周文建，童宗鹏，沈建平

(中国船舶重工集团公司第七一一研究所，上海 200090)

船舶传动装置多体动力学和有限元仿真技术

马炳杰，周文建，童宗鹏，沈建平

(中国船舶重工集团公司第七一一研究所，上海 200090)

目前，传动装置振动计算多采用集中参数法，未将轴系振动(扭转振动、横向振动与纵向振动)以及结构振动进行综合分析，与实际情况有一定的差别。本文以典型双机并车装置传动(包括柴油机、高弹性联轴器、万向轴、传动齿轮、主轴与输出负载)为研究对象，应用多体系统动力学理论对其激励特性进行研究，为传动装置有限元动力学响应分析提供输入条件。在完成传动装置多体动力学仿真分析的基础上建立传动装置有限元分析模型，然后对传动装置进行轴系振动和结构振动有限元动力学响应分析，并进行试验验证。同时，讨论转速和隔振刚度对传动装置结构振动的影响规律。最后，通过总结，初步形成船舶传动装置基于多体动力学和有限元仿真的振动特性预估方法，以完善和充实传动装置的研究方法和理论。

船舶;传动装置;振动控制;多体动力学;有限元

0 引言

船舶传动装置是实现舰船发动机与推进器(一般为螺旋桨)的能量传递，同时又将螺旋桨旋转产生的轴向推力通过轴系传给船体，推动船舶前进的系统，是舰船动力装置系统中必不可少的重要部件［1］。船舶在海上航行，会产生不同程度的振动。对于传动装置来说，如果所承受的激励较大，可能引起剧烈的振动，甚至影响船舶的运行，因此对传动装置的振动分析显得尤为重要。以往对船舶传动装置的动力学特性进行研究时，大多采用基于集中质量系统的计算分析法［2］。该方法对于简单传动装置运动规律的描述具有一定的准确性，然而，船舶传动装置的复杂性加上轴系振动与结构振动的耦合，基于集中质量系统的计算分析法难以准确描述传动系统及其部件的振动响应规律。综合应用有限元理论和多体动力学，成为研究轴系振动和结构振动的新方法。这种方法，在内燃机振动噪声的预估方面已经成为主流，但在船舶的传动装置振动预估方面应用较少。一方面，船舶传动装置传动链较长，各部件之间的连接关系难以确定;另一方面，船舶传动装置结构甚为复杂，从柴油机、隔振装置、齿轮箱一直到螺旋桨，组成部件较多，建模和计算工作量较大。因此，目前从事这方面的研究工作较少。文献［3］综合分析了船舶传动装置振动控制技术研究现状与发展趋势。文献［4－5］以柴油机推进系统为研究对象，分别单独采用多体动力学方法和有限元方法进行结构振动预估，然而并未采用2种方法综合进行分析，也未单独进行轴系振动分析。

本文采取基于多体动力学和有限元理论的综合方法对传动装置的轴系振动和结构振动特性进行研究。以船舶推进的典型形式——双机并车传动装置(包括柴油机曲轴、高弹性联轴器、万向轴、传动齿轮、主轴与输出负载)为研究对象，应用多体动力学理论对其运动学和激励特性进行研究，应用有限元法对传动装置进行动力学响应分析，并通过试验结果对该仿真结果进行验证。最后，通过对传动装置的多体动力学和有限元动力学响应分析进行总结，初步形成船舶传动装置基于多体动力学和有限元仿真的振动特性预估方法，以完善和充实传动装置的研究方法和理论。

1 传动装置多体动力学理论建模技术

对于多体系统中的柔性体，采用将零件的运动分解为整体(物体参考系)的刚性运动和相对于物体参考系的变形运动的相对描述法［3］。将柔性体看作是有限元模型的节点的集合，其变形运动近似地采用离散的有限个自由度位移来表示，在弹性小变形的范围内，该位移可用模态向量及相应的模态坐标的线性组合来描述。

假设柔性体第i个节点的位置为:

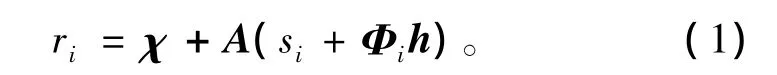
式中:χ为从整体坐标系原点到局部坐标系的位置矢量;A为局部坐标系相对于整体坐标系原点的方向余弦矩阵;si为第i个节点未变形前在局部坐标系的位置;Φi为第i个节点的模态振型分量;h为模态振幅向量。

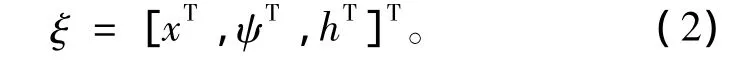
式中:x，y和z为局部坐标系相对于整体坐标系的位置;ψ，θ和φ为局部坐标系相对于整体坐标系原点的欧拉角;hm为第m阶模态振幅的振型分量。第i个节点的速度

从式(3)可得到动能和势能的表达式为:

然后使用拉格朗日方程就可获得柔性体方程式

式中:K和D分别为柔性体的模态刚度和阻尼矩阵。阻尼和刚度的变化只取决于变形。因此，刚体的平动和转动对变形能和能量损失没有影响。重力写成fg，λ为约束方程的拉格朗日乘子，Ω和Q为外部施加的载荷［4］。

2 传动装置多体动力学和有限元仿真模型建模技术

本文以船舶传动装置的典型形式——双机并车传动装置为研究对象(如图1)。该装置主要由2台柴油机分别通过高弹性联轴器、离合器、万向联轴器连接到并车齿轮箱上，在齿轮箱输出端通过过度轴与高弹性联轴器连接，然后高弹性联轴器与中间支承轴承连接，最后通过连接轴连接到磁粉测功器。传动装置运动机构由柴油机运动部件(活塞、连杆与曲轴)以及轴系运动部件(高弹性联轴器、万向联轴器、中间支承、传动齿轮、连接轴与输出负载)组成，由于运动机构并不是一个绝对的刚体，在周期性变化的爆发压力和运动质量的惯性力作用下将产生各种形态的振动，同时本文所讨论的传动装置结构形式复杂，运动传递链较长，很有可能破坏传动装置原有平衡状态，使机体和传动装置的振动和噪声显著增大。因此，在精确仿真传动装置动力学特性时，就应该充分考虑到传动装置的柔性效应。

图1 双机并车传动系统模型Fig.1 Model of twin—engine incorporation drive system

2.1 多柔体系统仿真模型的建立

通过在Ansys有限元软件中进行传动装置传动轴系(包括柴油机曲轴、高弹性联轴器、万向轴、传动齿轮轴、中间轴、尾轴等)的有限元模态分析获得其柔性体所需的模态信息，将包含有模型频率和振型的MNF文件调入多体动力学分析软件ADAMS，从而进一步在ADAMS软件中建立传动轴系的多柔体动力学仿真分析模型(如图2所示)。建模时，由于柔性体位置坐标采用模态坐标的线性组合形式，所以当有限元模型离散化程度较高，保留的模态数较多时，计算将保留每个节点频率和振型信息，这样就会使整个模型的计算规模变得十分庞大，对系统存储要求也有较高要求，所以应该在保证工程计算精度的要求下，尽可能地减少模型的离散化程度和模态信息数目。

2.2 激励力仿真分析

图2 传动装置轴系多柔体动力学模型Fig.2 Multi-body system dynamics model of drive system

对该传动装置多体动力学仿真计算，可得到活塞运动规律、连杆大端受力曲线、柴油机对支撑的作用力、高弹输出端振动扭矩的运动规律和动力学特性仿真结果，为后续强迫振动计算提供激励输入，其中的部分结果如图4～图7所示，图3为多体动力学仿真过程图。

图7 高弹输出端振动扭矩Fig.7 Output terminals torque of elasticity of coupling

3 传动装置轴系振动计算分析

实际上轴系的扭转振动、回转振动和纵向振动往往是耦合到一起的，传统的轴系振动分析方法将其割裂开进行分析是片面的。因此本文应用Abaqus商用有限元分析软件对传动轴系振动进行综合分析。这里应用Newmark隐式积分法，对前面建立起来的有限元模型进行传动轴系振动计算分析，求解传动装置轴系动力学响应，分析其动态特性，激励力采用2.2节中的计算结果。经过仿真计算，得出尾轴末端扭转角度和高弹输出端扭振应力，如图8和图9所示。

4 传动装置结构振动计算分析

4.1 传动装置转速对结构振动的影响

由于柴油机的转速是影响船舶动力传动装置振动噪声的最重要的因素之一，因此针对不同的转速进行了仿真计算。图10为转速分别为800，1200与1600 r/min的仿真计算结果。由图中曲线分析可知，不同转速下的振动速度响应曲线形状基本一致，但传动装置的振动响应对柴油机转速的变化十分敏感，具体表现如下:

1)随着柴油机转速的变化，传动装置的振动速度响应频谱发生了明显的变化。在低于50 Hz的频段内，3种不同转速的响应差别均较大，最大值为35 dB;在高于 50 Hz的频段内，1200 r/min与 1600 r/min的响应差别较小，而与800 r/min的响应差别较大，最大值为27 dB。

2)传动装置特征频率随着柴油机转速的降低而向低频移动。与此同时，传动装置的振动幅值也随之下降。

图10 柴油机转速对传动装置振动速度谱的影响Fig.10 Infection of rotate speed to system velocity

4.2 隔振刚度对传动装置结构振动的影响

图11以对数谱的形式给出了隔振刚度分别为1.6×106，1.2×106以及1.0×106N/m时的振动响应结果。由图11可见，传动装置的振动响应对隔振刚度的变化也十分敏感。具体为:

1)随着刚度的变化，传动装置的振动速度响应频谱发生明显变化。在低于40 Hz的频段内，3种不同刚度的响应差别较小;在高于40 Hz的频段内，3种不同刚度的响应振动幅值差别较大，其中在频率为173 Hz时，1.6×106，1.2×106以及1.0×106N/m时的振动幅值差分别为12 dB和13 dB。

2)传动装置特征频率随着隔振刚度的降低而向低频移动。与此同时，传动装置的振动幅值随隔振刚度的降低而增大。

图11 隔振器刚度对传动装置振动速度谱的影响Fig.11 Infection of isolator stiffness to tsystem velocity

5 传动装置有限元仿真方法试验验证

5.1 传动装置仿真计算结果和试验数据对比

将传动装置轴系振动和结构振动有限元计算结果与试验测试数据进行对比，以验证该计算方法的精确性。传动轴系振动计算是取高弹性联轴器输出端扭振应力、万向联轴器扭振应力仿真计算和试验数据进行对比，分别如图12～图14所示。传动装置结构振动计算主要是柴油机机脚的垂向振动速度与试验测试结果进行对比。表1是仿真计算结果和试验结果的对比。

图12 高弹输出端扭振应力仿真计算和试验对比Fig.12 Contrast between experiment and simulation of elasticity of coupling

表1 仿真计算结果和试验结果的对比Tab.1 Contrast of results between experiment and simulation

5.2 结果分析

1)根据传动装置动力学仿真计算结果和试验结果的对比可看到，轴系扭振应力最大值的仿真结果和试验结果相对误差为21.8%，万向联轴器扭振应力最大值的仿真结果和试验结果相对误差为25.8%;机组垂向振动速度最大值仿真计算结果与试验结果相对误差为10.9%。仿真结果和试验结果较为接近，说明本文所建立的传动装置柔体模型和有限元模型是合理的，所采用的多体动力学和有限元仿真方法比较好的反映了轴系的实际动态特性。

2)影响传动装置多体建模及其分析、有限元建模及其分析，进而导致仿真结果与实验结果存在误差的主要因素有以下几个:

①高弹性联轴器中橡胶材料的高度非线性，导致其实际刚度与仿真计算中输入的参数存在误差;

②齿轮的啮合在实际中非常复杂，存在瞬时冲击等特性，在有限元仿真计算中难以精确模拟;

③传动装置模型的结构简化，不可避免产生一些误差;

④由于柴油机的复杂性，通过多柔体动力学分析得到的边界条件与实际情况必然存在一定误差;

⑤阻尼固存于试验数据中，但在有限元计算中难以精确模拟。

6 结语

本文以双机并车动力传动装置为研究对象，应用多体动力学理论对其激励特性进行研究，应用有限单元法对传动轴系振动和结构振动进行动力学响应分析，讨论了转速和隔振刚度对传动装置结构振动的影响规律，并进行了试验验证。通过总结，初步形成船舶传动装置基于多体动力学和有限元仿真的振动特性预估方法。

1)仿真模型激励的输入和耦合副的施加是多体动力学仿真的关键，因此认清柴油机激振源的性质及其对结构动力学特性的影响、激励沿轴系的传递途径是进行传动装置动力学分析研究的出发点。特别的，对于耦合副的施加(活塞与汽缸、曲轴与连杆、齿轮副、高弹、万向以及轴系与支撑等之间的耦合)，要与实际情况尽量相符合。

2)进行有限元分析计算必须首先建立正确的有限元模型。本文通过利用CAD软件建立了传动装置(包括柴油机曲轴、高弹性联轴器、万向轴、传动齿轮、主轴与输出负载)的实体模型。由实际结构的复杂性，本文在不影响分析结果精度的基础上对结构进行了合理的简化以降低计算规模，为后期进行整个装置的结构动力学分析计算奠定基础。

3)分析模型边界条件的确定与施加会直接影响到结构动力学响应分析结果的准确性。本文利用多体动力学计算结果合理确定了激励因素，并在合理建立有限元模型的基础上进行了传动装置基于Newmark隐式积分法的有限元动力学响应分析，获得了结构的动态特性，从而对实际使用过程中可能反映出的传动装置振动情况进行了初步预测。

4)标准化、规范化是加速技术进步和提高产品质量的重要手段。探索并建立传动装置多体动力学和有限元仿真分析技术规范和多体动力学仿真分析技术规范，进一步完善和充实传动装置的研究方法和理论，将是今后进一步进行的工作。

［1］周春良.船舶轴系振动研究［D］.哈尔滨:哈尔滨工程大学，2006.

［2］严济宽.机械振动隔离技术［M］.上海:上海科学技术文献出版社，1985.

［3］沈建平，周文建，童宗鹏.船舶传动装置振动控制技术研究现状与发展趋势［J］.舰船科学技术，2010，32(8):7－12.

SHEN Jian-ping，ZHOU Wen-jian，TONG Zong-peng.Status and trends about research of vibration control in ship transmitting device［J］.Ship Science and Technology，2010，32(8):7 －12.

［4］童宗鹏，周文建，王国治，等.船舶传动系统结构振动控制技术研究［J］.噪声与振动控制，2009，29(6):136－139.

TONG Zong-peng，ZHOU Wen-jian，WANG Guo-zhi，et al.Research on vibration control of ship drive system［J］.Noise and Vibration Control，2009，29(6):136 －139.

［5］孙少龙，沈建平.传动装置结构振动计算和试验研究［J］.噪声与振动控制，2010，30(5):47 －50.

SUN Shao-long，SHEN Jian-ping.Numerical calculation and experimental research on vibration control of ship's drive system［J］.Noise and Vibration Control，2010，30(5):47－50.

［6］陆佑方.柔性多体系统动力学［M］.北京:高等教育出版社，1996.

LU You-fang.Dynamics of flexible multibody systems［M］.Beijing:Higher Education Press，1996.

［7］李军，邢俊文，覃文洁.Adams实例教程［M］.北京:北京理工大学出版社，2002.

Multi-body system dynamics analysis and finite element simulation on marine power transmission system

MA Bing-jie，ZHOU Wen-jian，TONG Zong-peng，SHEN Jian-ping
(The 711 Research Institute of CSIC，Shanghai 200090，China)

The lumped parameter method is widely adopted in the vibration calculation of the transmission system currently.The aggregate analysis of the torsional vibration of the shafting，the transverse vibration，the extensional vibration and the structural vibration are not undertaken.In this thesis，the drive characteristics are researched applied the theory of the multi-body dynamics and the input conditions are supplied to the dynamic response analysis of the finite element model based on typical two-engined joint operating device(include diesel engine，the elasticity coupling，cardan shaft，driving gear，main shaft and output load).Through the dynamic simulation with transmission system，the finite element analysis model of the transmission shafting is established，and the dynamic responses of the shafting vibration and structural vibration are analyzed，and the experimental verification was proceeded.Meanwhile，the transmission characteristics of the structure vibration about transmission system are revealed.The influence regulations about the parameters of the elasticity couplings，rubber isolators to the structure vibration are discussed.Finally，through the analysis of the multi-body dynamics and the finite element dynamic responses，the simulation analysis method about the vibration of the transmission system is formed so as to perfect and enrich the research approach and theory of the transmission devices.

marine;transmission system;vibration control;multi-body system dynamics;FEM

U664.2;TK421.4

A

1672－7649(2011)12－0051－06

10.3404/j.issn.1672－7649.2011.12.011

2011－03－03;

2011－06－17

马炳杰(1981－)，男，博士研究生，工程师，从事动力装置振动噪声抗冲击技术研究。