基于分数低阶统计量的卡尔曼滤波目标跟踪算法

石一鸣，张安清，张 琦

(1.91550部队，辽宁 大连 116023;2.海军大连舰艇学院信息与通信工程系，辽宁大连 116018;3.海军大连舰艇学院博士研究生队，辽宁大连 116018)

基于分数低阶统计量的卡尔曼滤波目标跟踪算法

石一鸣1，张安清2，张 琦3

(1.91550部队，辽宁 大连 116023;2.海军大连舰艇学院信息与通信工程系，辽宁大连 116018;3.海军大连舰艇学院博士研究生队，辽宁大连 116018)

针对杂波干扰环境中的非高斯特性，发现海杂波噪声、闪烁噪声等具有显著尖峰的非高斯噪声，可以采用α稳定分布建立更符合实际的噪声模型。根据统计信号处理最新理论和技术，利用p阶分数相关和分数低阶协方差替代传统相关和协方差来改进Kalman滤波器，优化获得基于分数低阶统计量的Kalman滤波目标跟踪新算法(FLOS－KF)。仿真验证了FLOS－KF滤波跟踪新算法可以更好地适应非高斯复杂环境，得到稳健的跟踪效果。

目标跟踪;舰艇火控系统;Kalman滤波;α稳定分布;分数低阶统计量

0 引言

大多数目标跟踪算法均要求观测噪声和系统噪声为独立或相关的高斯噪声，而在实际应用中所观测到的信号并不是高斯分布的，例如雷达闪烁噪声、海杂波噪声、海洋水声环境噪声等。这些噪声均具有显著尖峰特性。在这种非高斯噪声环境下，若仍然采用高斯假定，将会导致在高斯的假定下设计的系统性能退化、甚至无法工作。针对此类问题，文献［1］采用t分布或者高斯分布与其他分布(如拉普拉斯分布)的合成对闪烁噪声建模，但仍然使用卡尔曼滤波器，该算法的跟踪性能也很难保证;文献［2］对闪烁噪声采用不同方差的高斯噪声加权来建模，提出了基于UKF的机动目标跟踪方法，并应用其跟踪具有高斯噪声和闪烁噪声的机动目标。而Georgiou等［3］用α稳定分布对脉冲(尖峰)状噪声建模，由于α稳定分布能非常好地与实际数据相吻合，因此在具有脉冲特性的信号或噪声建模方面受到了广泛的关注。本文将雷达闪烁噪声和海杂波噪声采用α稳定分布建模，结合机动目标跟踪问题应用分数低阶统计理论进一步研究，以获得新的机动目标跟踪滤波算法，满足目标跟踪鲁棒性需求。

1 α稳定分布过程与特性

正是由于α稳定分布能非常好地与实际情况相吻合，是一种能保持自然噪声过程的产生机制和传播条件的极限分布，它为具有尖峰或偶然脉冲类信号和噪声提供了非常有用的理论工具，是一种更加广义化的高斯分布(或者说高斯分布是α稳定分布的一个特例)。其主要区别是α稳定分布的分布密度比高斯分布密度有更厚的拖尾，α稳定分布的这种特征正是用于对具有冲激特征的信号和噪声建模的主要原因之一，是一种非常灵活的建模工具［4］。它有1个特征指数参数α(0＜α≤2)控制拖尾的厚度，α值越小表明冲激越大，而α接近2则更具高斯特性;当α=2，即为高斯分布，如图1所示高斯信号和分数低阶α稳定分布信号(α=1.5)示例，可见后者的冲激性明显。

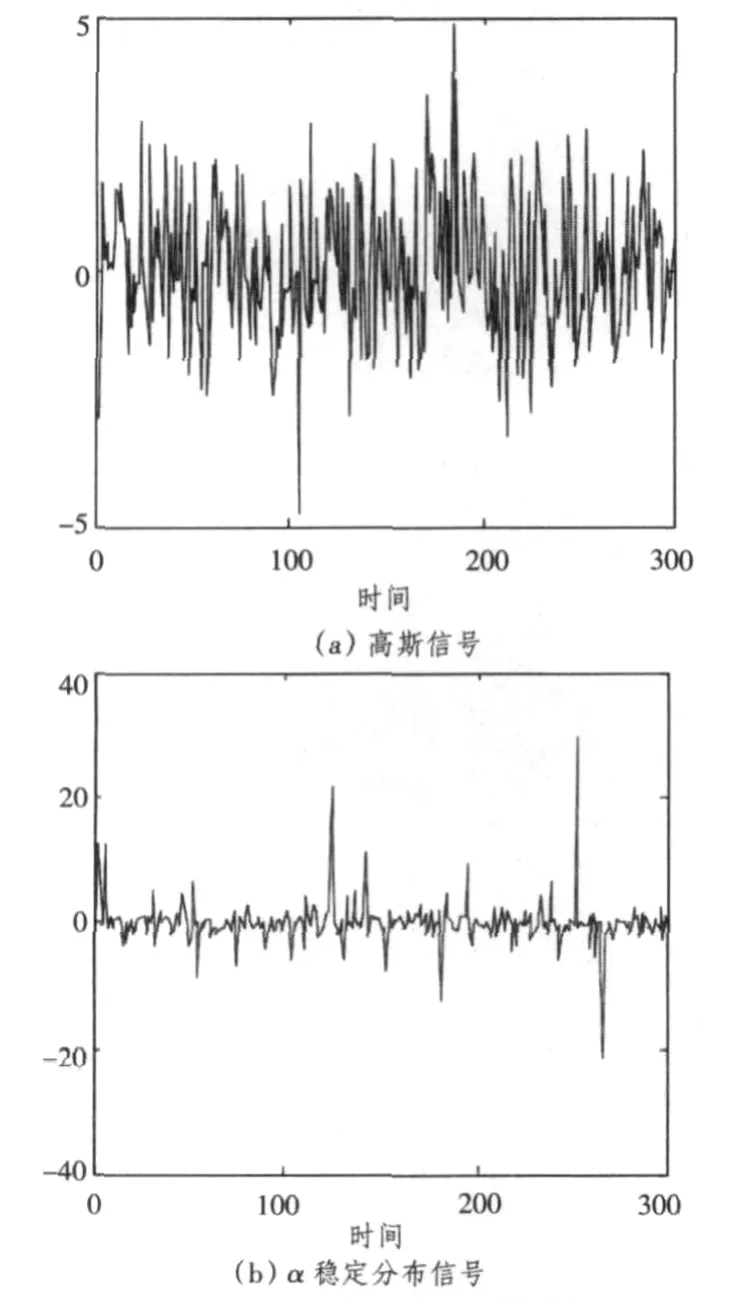
图1 高斯信号和α稳定分布信号的比较Fig.1 The comparison of Gaussian signal and α stable distribution

2 分数低阶统计量及最小分散系数准则

根据统计信号分析的理论，大多数信号处理的统计理论和方法都是建立在协方差基础上的。如有用信号的预测、观测信号的滤波与平滑。然而，若α稳定分布的特征指数为0＜α＜2，则只有阶数小于α阶的矩是有限的，其方差(或2个随机过程的协方差)及高阶统计量都是不存在的。于是，人们研究低于二阶的分数阶统计量，称为分数低阶统计量(FLOS)，其范围为(0，2)。

对于2个α稳定分布随机信号或过程，有2类分数阶协方差［5］表示如下:

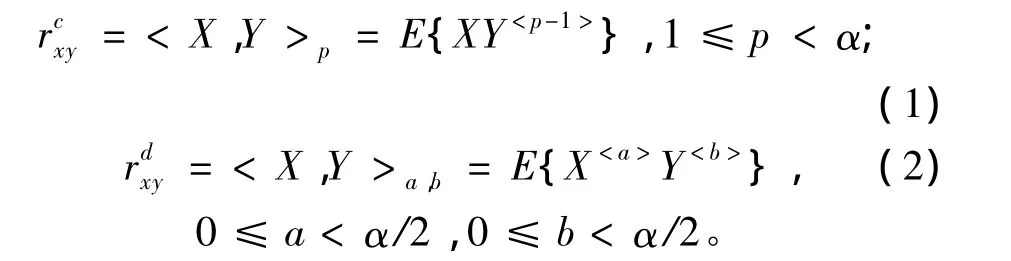
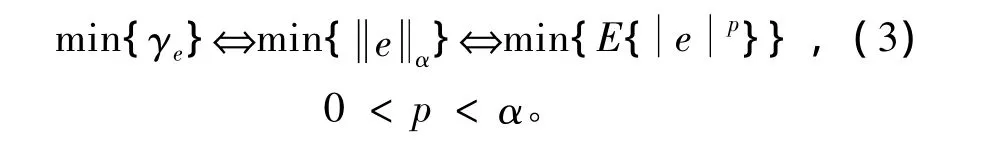
3 卡尔曼滤波目标跟踪新算法

在高斯假设条件下的统计信号处理问题是从给定观测值中找到未知变量y的最佳估计y^。最常使用的最佳估计准则是最小均方准则(MMSE)。在这个准则下，最佳估计使得估计误差的均方差最小［6］。而对于α稳定分布过程，MMSE准则就不再适用了，因为估计误差不再具有有限方差。但是可以把MMSE准则推广到α稳定分布过程中。当y^是y的最佳估计时，若令e=y－y^，从α稳定分布的稳定性定理［7］可知，e也是α稳定分布的。若e的分散系数为γe，则有min{eα}等价于min{γe}。也就是说，当估计误差的分散系数到达最小时，y^就是y的最佳估计。这个准则被称为最小分散系数准则，简称为MD准则。最小化分散系数也等价于最小化分数低阶矩。于是，可以得到如下3种等价关系

目标跟踪问题也是用有限观测时间间隔内收集到的观测值，即Z(1)，Z(2)，…，Z(n－1)来估计线性离散时间动态系统的状态X。设系统动态模型［8］如下:

1)状态方程

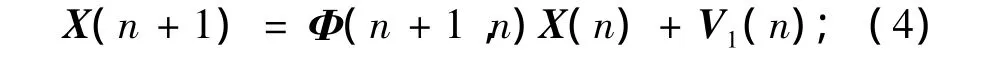
2)观测方程

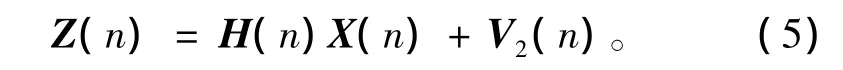
其中:X(n)为M维状态向量，卡尔曼滤波器的目的是对其状态向量进行最佳估计;Φ(n+1，n)为M×M维状态转移矩阵;V1(n)为M维过程噪声向量;Z(n)为N维观测向量;H(n)为N×M维观测矩阵;V2(n)为N维观测噪声向量。不同噪声环境下，V1(n)与V2(n)特性不一样，但都假设它们不相关。这里，根据前面提出的理由，具有显著杂波尖峰环境下的雷达目标跟踪观测或空中目标观测存在闪烁噪声的情况下，建立V1(n)与V2(n)为α稳定分布模型能更好地描述［9－10］。

传统Kalman滤波算法根据观测向量Z(n)对状态向量X(n)进行估计，使估计误差均方差最小。需要计算新息过程的二阶矩及噪声过程的二阶相关矩，而这些量在SαS分布噪声下是不存在有限值的。因此，对SαS分布噪声模型下的目标跟踪滤波提出改进方法，即利用最小分散系数(MD)准则替代最小均方(LMS)准则，利用p阶分数相关和分数低阶协方差替代传统相关和协方差［11－12］。改进Kalman滤波算法具体做法是以估计误差的p范数(lp范数，0＜p＜α)为性能函数，使其最小优化获得基于分数低阶统计量的Kalman滤波目标跟踪算法(FLOS－KF)。

根据观测值Z(1)，Z(2)，…，Z(n－1)估计X(n)，记为X^(n，n－1)。此预测误差向量

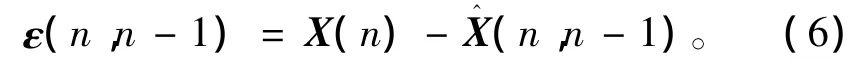
定义预测误差的p范数［6］函数(标量)

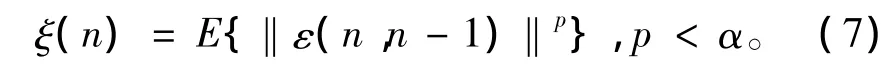
ξ(n)就是改进Kalman预测时的性能函数。改进Kalman预测估计在于使预测误差函数的p范数ξ(n)最小。这种估计不是传统的最佳Kalman预测估计，而是在非高斯SαS分布噪声下的次优估计。准则为:

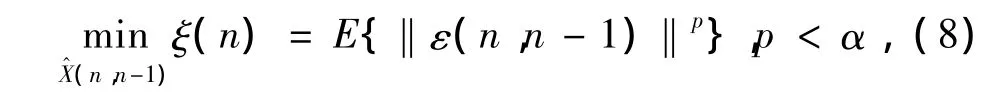
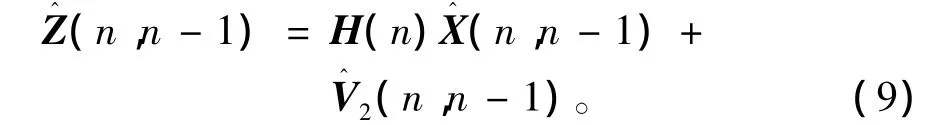
这是根据Z(1)，Z(2)，…，Z(n－1)估计的Z(n)，由于V2(n)与Z(1)，Z(2)，…，Z(n－1)不相关，式(9)变为:

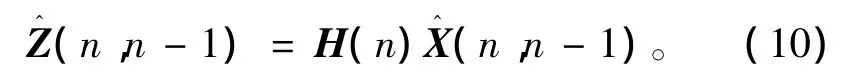
对于n时刻的观测值Z(n)所带来的新息［8］为:

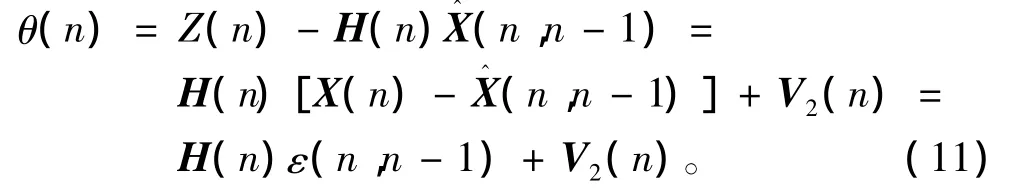
式中:θ(n)为新息向量。

SαS分布脉冲噪声下的新息过程具有如下性质:

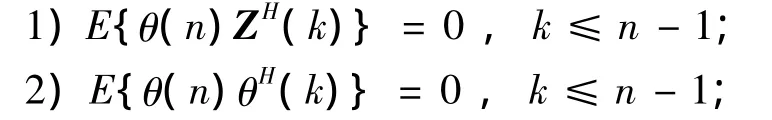
3)由于观测噪声V2(n)是SαS分布脉冲噪声，所以E{|θ(n)|2}=∞，即新息过程为无限方差的随机过程。但根据信号分数低阶统计处理理论，若0＜p＜α，则E{|θ(n)|p}＜∞，表示新息过程具有有限的p阶矩。

新息过程的分数低阶相关阵定义下式，称为新息分数低阶相关阵

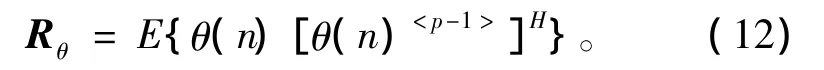
状态向量的一步预测最直接的方法就是用新息过程θ(1)，…，θ(n)的线性组合构造，即

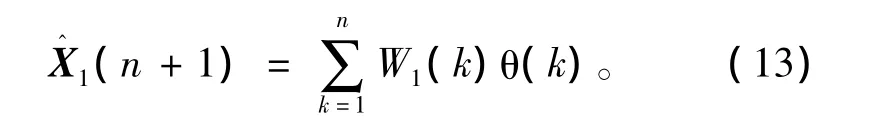
其中，W1(k)表示一步预测对应的权矩阵。根据新息过程的正交性推导得

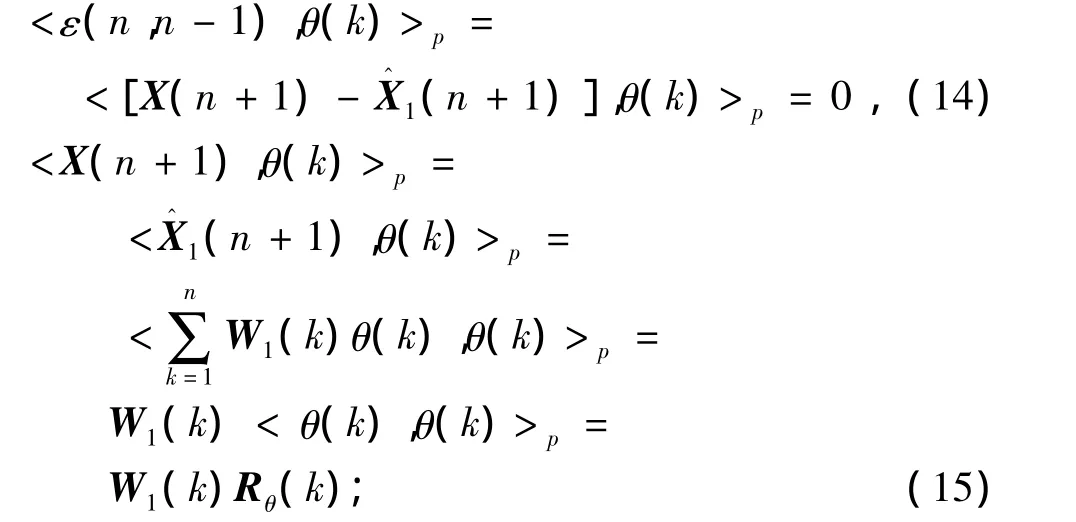
因此

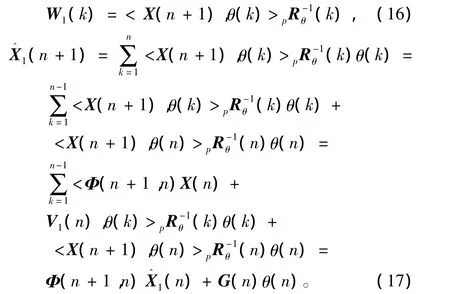
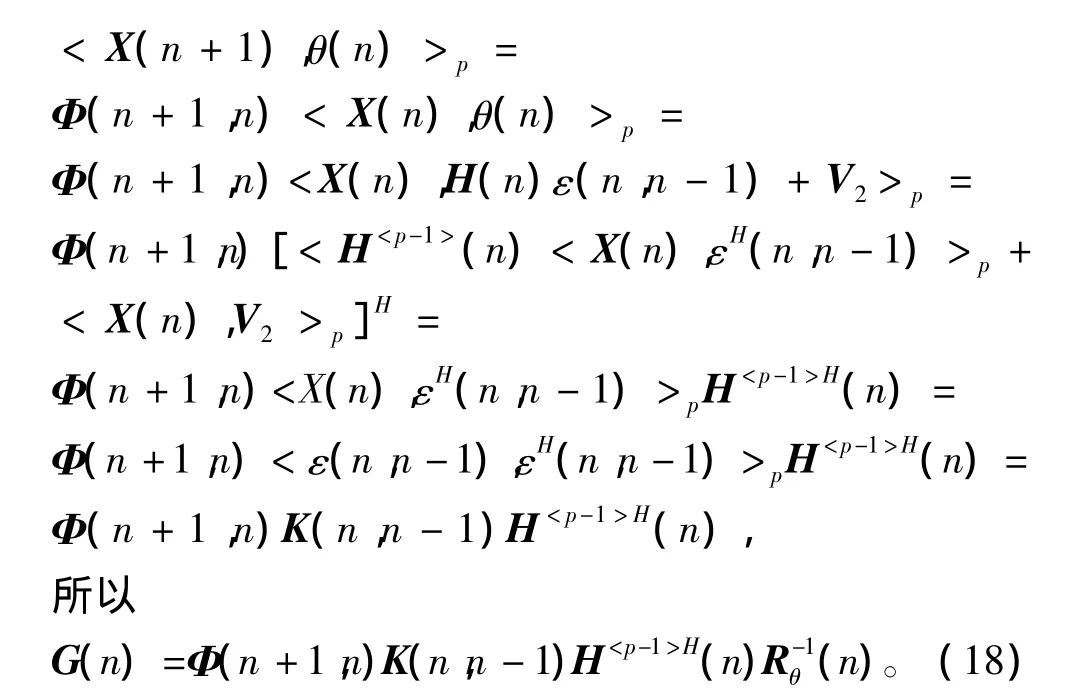
为实现自适应滤波算法，还需推导K(n+1，n)递推公式。考察状态向量的预测误差，

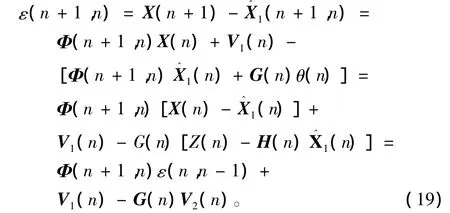
求式(19)状态向量一步预测误差向量的分数阶相关矩阵，容易证明:

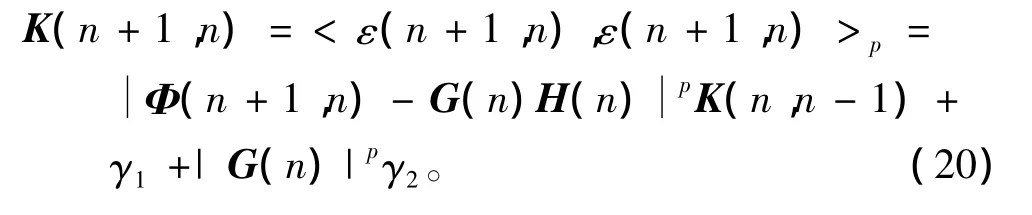
4 仿真结果与分析

为说明在尖峰非高斯噪声环境下目标跟踪滤波存在的问题，检验本章提出的基于分数低阶统计量卡尔曼滤波目标跟踪改进算法的效果，首先进行仿真实验一，以X轴为例，假定目标沿X轴方向匀速运动，观测噪声施加α稳定分布噪声，噪声特征指数取α=1.6。分别采用典型Kalman滤波跟踪和改进的基于分数低阶统计量FLOS-Kalman滤波跟踪方法。图2(a)和(b)分别表示在尖峰非高斯噪声环境下典型Kalman滤波和改进的FLOS-Kalman滤波跟踪相同环境条件下的目标情况。图3(a)和(b)是随机产生尖峰非高斯噪声下的另一2种方法跟踪目标的比较效果。图4(a)和(b)是高斯噪声下两种方法跟踪情况。表1归纳了典型Kalman滤波跟踪与改进FLOSKalman滤波跟踪2种方法在高斯噪声和尖峰噪声环境下50次仿真跟踪误差均方根值。

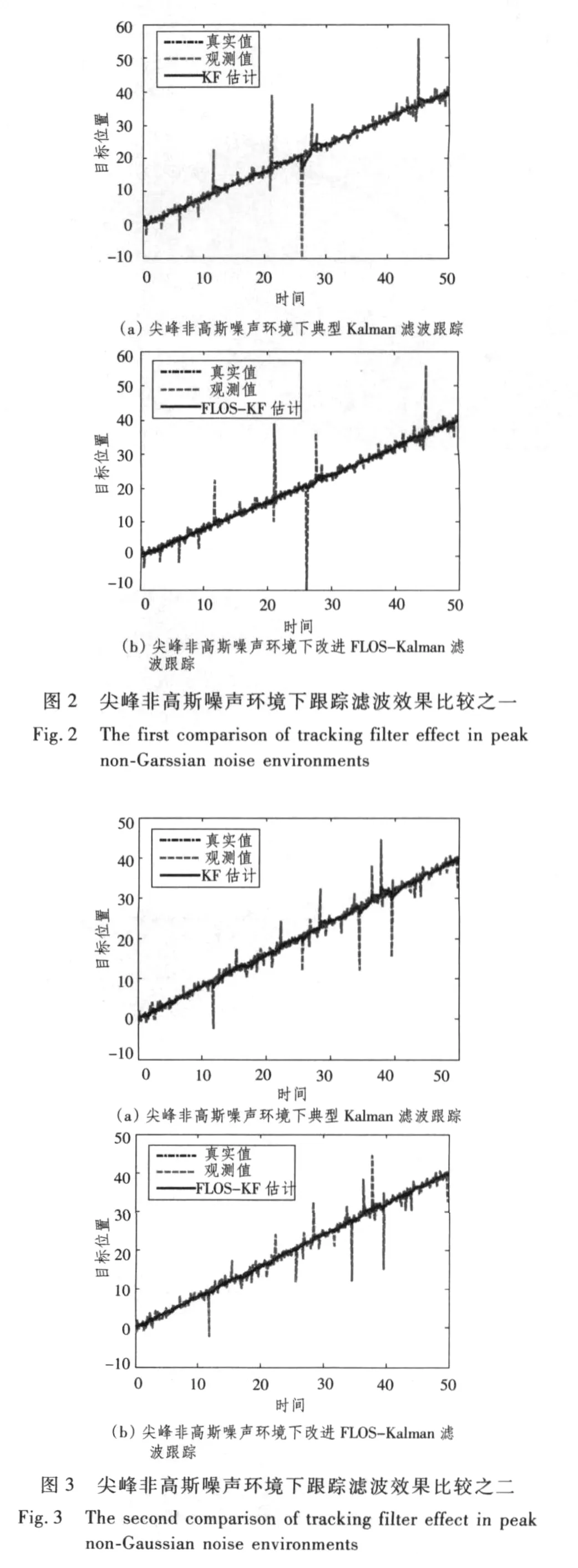
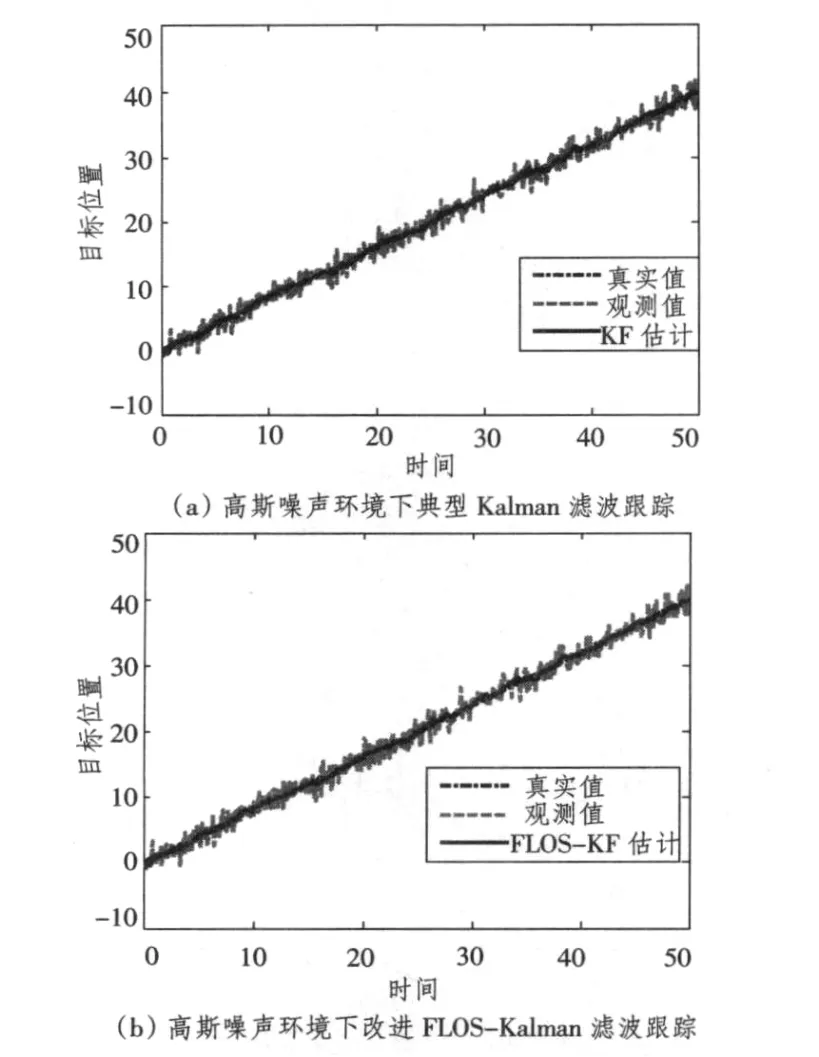
图4 高斯噪声环境下跟踪滤波效果比较Fig.4 The comparison of tracking filter effect in Gaussian noise environments

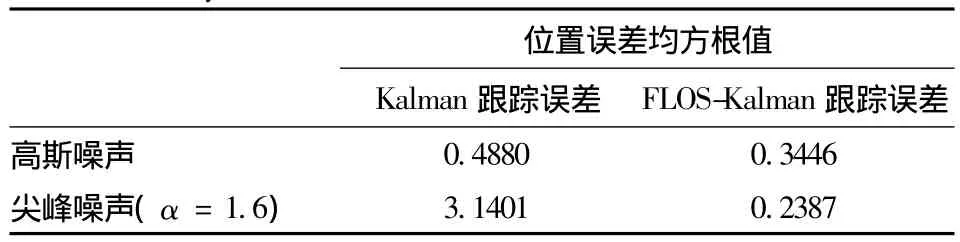
表1 2种目标跟踪算法50次仿真位置误差均方根值Tab.1 The position RMSE of two targe tracking simulations by 50 times

图2和图3是不同强度尖峰噪声环境下的Kalman与FLOS-Kalman跟踪的2次实验。图4是高斯噪声环境下的Kalman与FLOS-Kalman跟踪。由图2～图4以及表1可以看出，在非高斯情况下，与Kalman滤波相比，改进的FLOS-Kalman滤波算法表现出更高的精度和更强的抗噪声性能;在高斯情况下2种算法跟踪性能相当，从而表明改进FLOS-Kalman跟踪方法，无论在尖峰噪声(非高斯性)，还是在高斯噪声条件下，均具有较好的抗噪声性能，都能稳定跟踪，其鲁棒性比较好。

5 结语

本文主要对非高斯脉冲噪声特性环境下机动目标跟踪算法进行了研究。对α稳定分布过程性质、分数低阶统计量和最小分散系数准则的概念进行了分析，重点研究了采用α稳定分布规律对海杂波噪声、闪烁噪声等非高斯噪声建模，利用p阶分数相关和分数低阶协方差替代传统相关和协方差来改进Kalman滤波器，设计以估计误差的p范数为性能函数，推导出基于分数低阶统计量的Kalman滤波目标跟踪算法(FLOS－KF)。我们相信，这一研究工作的进一步工程化有利于舰载指控系统目标探测与跟踪，该方法的研究具有重要的理论和军事应用价值。

［1］DAEIPOUR E，BAR-SHALOM Y.An interacting multiple model approach for target tracking with glint noise［C］.Record of the IEEE National，Radar Conference，1994.

［2］朱志宇.基于UKF的闪烁噪声机动目标跟踪［J］.计算机仿真，2007，24(11):120 －123.

ZHU Zhi-yu.Unscented Kalman filter for maneuver target tracking under glint noise［J］.Computer Simulation，2007，24(11):120－123.

［3］GEORGIOU P G.Alpha-stable modeling of noise and robust time-delay estimation in the presence of implusive noise［J］.IEEE Transactions on Multimedia，1999，1(3):291 －301.

［4］孙仲康.雷达数据数字处理［M］.北京:国防工业出版社，1983.

［5］SHAO M，et al.Signal processing with fractional lower order moments:Stable processes and their applications［J］.Proceedings of the IEEE，1993，87(1):986 －1010.

［6］CHAMBERS J A，TANRIKULU O，CONSTANTINIDES A G.Leastmean mixed-norm adaptive filtering［J］.Electronics letters，1994，30(19):1574 －1575.

［7］BODENSCHATZ J S，NIKAS C L.Symmetric alpha-stable filter theory［J］.IEEE Transactions on Signal Processing.1997，45(9):2301 －2306.

［8］张贤达.现代信号处理［M］.北京:清华大学出版社，2002.

［9］张安清，邱天爽，章新华.α稳定分布的水声信号处理新方法［J］.电子与信息学报，2005，27(8):1201 －1204.

ZHANG An-qing，QIU Tian-shuang，ZHANG Xin-hua.A new underwater acoustic signals processing approach to astable distribution［J］. JournalofElectronics and Information Technology，2005，27(8):1201 －1204.

［10］MA X Y.Robust signal processing in impulsive noise with stable distributions:estimation，identification and equalization［D］.USA:A BELL＆Howellinformation company，University of southern California，1996.

［11］查代奉，等.一种基于分数低阶协方差矩阵的波束形成新方法［J］.通信学报，2005，(7):16 －20，55.

ZHA Dai-feng，et al.New beamforming method based on fractional lower order covariance matrix［J］.Journal of China Institute of Communications，2005，(7):16 － 20，55.

［12］吕泽均，肖先赐.基于时延分数阶相关函数时空处理的子空间测向算法［J］.信号处理，2003，(1):51 －54.

LV Ze-jun， XIAO Xian-ci.A subspace-bsed direction finding algorithm using temporal and spatial processing of time lag fractonal order correlation function［J］.Signal Processing，2003，(1):52 －54.

Optimized fractional lower order covariance Kalman filter algorithm

SHI Yi-ming1，ZHANG An-qing2，ZHANG Qi3
(1.91550 Unit，Dalian 116023，China;2.Department of Information and Communication Engineering，Dalian Naval Academy，Dalian 116018，China;3.PHD Team，Dalian Naval Academy，Dalian 116018，China)

Aimed at non-Gaussian characteristics in clutter jamming environment，this paper studies significant peak non-Gaussian noise for sea clutter noise and glint noise described by alpha stable distribution，establishing noise model accord with reality.According to the lastest theory and technology of statistics signal processing，make use of p order fractional associated and fractional lower order covariance to modify Kalman filter，optimized fractional lower order covariance Kalman filter new algorithm，which is introduced to the target tracking for complicated non-Gaussian situation and achieve the solid tracking effect.

target tracking;ship fire control system;Kalman filter;α stable distribution;fractional lower order statistics

TN949.6+3

A

1672－7649(2011)12－0028－05

10.3404/j.issn.1672－7649.2011.12.006

2011－03－14;

2011－10－11

石一鸣(1985－)，女，硕士研究生，助理工程师，研究领域为雷达总体、测量与控制等。