自然环境下路面裂缝的识别
马常霞 , 赵春霞, 狄 峰, 李旻先
(1. 南京理工大学计算机科学与技术学院,江苏 南京 210094;2. 淮海工学院计算机工程学院,江苏 连云港 222005)
道路交通在国民经济和人民生活中占有重要的地位。随着道路建成后的不断使用,对其合理有效的保养和维护就成为主要问题。定期调查道路路面状况,并做出相应的维护措施,以便在路面病害出现的早期就发现它、修缮它是路面维护的基本思路。传统的基于人工视觉检测病害的方法花费大、效率不高、影响交通、检测结果不可靠存在因人而异的现象,因此不能适应道路发展的需要。迫切需要提出一种快速有效的路面病害检测方法。
初期使用摄像机的路面裂缝识别系统是一种基于人工或计算机辅助的人工评价,即半自动化的检测。由工作人员检查存储在计算机硬盘上的路面图像,在图像上标注出裂缝,再由计算机进行统计。后来的计算机辅助半自动裂缝识别系统通过一些路面图像处理算法进行裂缝识别,提高了系统自动化水平。这些算法的基本目的是从一个二值图像中抽取裂缝特征。二值图像一般通过确定一个最佳阈值来得到,大于阈值的像素被认为是背景,设为白色像素;小于阈值的认为是裂缝,设为黑色像素,从而提取出裂缝。但是,由于路面图像中存在许多随机的噪声信息,确定一个适用于所有路面图像的阈值很困难,这样的处理并不能很准确地识别裂缝。所以,工作人员还必须仔细检查处理过的图像,人工纠正漏检和误检。
近年来,基于图像的路面病害自动检测已成为各国竞相研究的课题。它利用高速度、高精度的摄像机快速的拍摄路面图像,利用计算机快速处理,得到病害信息。目前主要的裂缝检测算法主要有人工种群算法[1]、多级拟合机制的检测方法[2]、基于三维地形模型的路面裂缝自动检测算法[3]、基于高速公路裂纹局部线性特征内容的脊波变换域算法研究[4]。这些算法都在一定程度上对常规裂缝检测算法有所改进,但均存在难以克服大量随机分布的噪声的影响,对一些轻微裂缝及网状裂缝仍然不能取得预期的效果,而且运算量过大,不利于对大量的路面图像的处理。
本文提出一种基于分数阶微分演算和图像形态学的路面图像增强及检测病害的方法。首先由于分数阶微分运算在加强信号高中频成分的同时,也对信号的甚低频成分进行了非线性保留,所以通过分数阶微分运算增强路面图像,可以使处于平滑区域的弱信号裂缝病害信息得以加强。然后在此基础上通过一组中值滤波过滤店大量的随机噪声,利用形态学算子检测出裂缝边缘,并细化提取出最终的裂缝骨架。
1 分数阶微分运算应用于图像处理
长期以来,分数阶微分主要被数学家作为一种纯数学理论来研究。由于没有得到实际应用背景的促进,发展相对比较缓慢。在近几十年里,分数阶微分理论才在化学、电磁学、控制学、材料科学和力学中引起广泛关注并做了一些尝试性的应用。将分数阶微分应用于图像信号处理,在国内外还是一个新的研究领域。
1.1 分数阶微分的定义
常用的分数阶微分定义有三种,即G-L型分数阶微分,R-L型分数阶微分,Caputo型微分。
G-L定义将连续函数的整数阶微分的阶数通过对原整数微分的差分近似递推式求极限推演而推广到分数。其定义如下[5]:
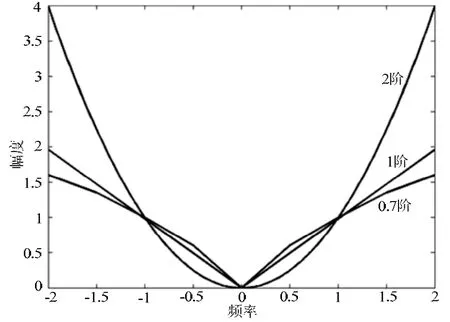
如函数 f (t)∈(a, t)(a 从信号处理的角度看,信号的分数阶微分的物理意义可以理解为广义的调幅调相,其振幅随频率呈分数阶幂指数变化,相位是频率的广义Hilbert变化。图1示出1阶、2阶和分数阶微分的幅频特性曲线[6]。 从图1中可以看出微分运算都有提升信号高频的作用,且随频率和微分阶数的增加呈非线性急速增长,同时对信号的甚低频有削弱作用。从图中明显看出 2阶微分对信号高频成分的提升远大于1阶微分,且对甚低频信号的削弱也明显强于1阶微分。对于分数阶微分当0 图1 信号微分的幅频特性曲线 表明分数阶微分在加强信号高中频成分的同时,也对信号的甚低频成分进行了非线性保留。对于图像而言,平滑区域即邻近的像素值基本相同的区域对应于信号的低频;图像纹理区域即邻近的像素值发生一定变化的区域对应于信号的中频;图像边缘和噪声区域即邻近的像素值发生较大变化的区域对应于信号的高频。从图中同样可以看出当微分阶数减小到0.1阶后,微分运算对信号高频的提升和信号中频的加强幅度都不是很大。 一般来说,在采集到的路面图像中包含两类对象:一是状况良好的路面,即背景;另一个是裂缝等病害,即识别的目标。因此,数字图像可分为两类像素集:代表背景的像素和代表裂缝等病害的像素。理想状况下,裂缝应该比背景更暗。但是由于许多因素的影响,会有所变化。具体的情况有: (1)由于路面材料的不均匀性,正常路面的纹理不均匀。因此,所采集的图像背景颜色本身有较大地变化。 (2)裂缝图像也有同样的情况。由于严重程度不同,其大小、面积也不同。如果裂缝中有与背景颜色相近甚至更亮的比较大的颗粒,也会导致裂缝图像颜色的变化。但总的来说,裂缝图像比正常路面的暗。 (3)代表裂缝的像素数量远远小于代表背景的像素数量。 (4)正常路面的灰度值与裂缝的灰度值有部分重叠。 (5)由于自然和人为因素的影响,复杂的背景噪声一般都叠加在有用的路面数据之中,所以必须进行滤波来减少噪声,增强裂缝边缘。 基于以上这些路面图像特性,可以采用有针对性的处理方法。本文从分数阶微分差值定义着手,构建了适合路面图像增强的分数阶微分掩模算子,通过中值滤波去除孤立噪声,最后利用形态学算子检测出裂缝。 2.1.1 分数阶微分差值定义 根据式(1),若一元信号f (t)的持续期为t∈[a,t],将信号持续期[a, t]按单位等分间隔h=1进行等分,所以可以推导出一元信号f (t)分数阶微分的差值表达为式(3)所示。 对数字图像f (x, y),其偏分数阶微分为式(4)和式(5)所示。 2.1.2 路面图像的分数阶微分掩模运算 二维数字图像信号中x和y的持续期间分别为x∈[x1, x2],y∈[y1, y2],对图像的分数阶微分运算从水平、垂直和斜向45º方向进行。根据式(4)和式(5)构造滤波器,获得3*3、5*5、7*7,…,(2*n+1)*(2*n+1)等尺寸的八方向分数阶微分算子。 本文使用了5*5的分数阶微分掩模算子如图2所示,对图像进行空间滤波处理,掩模中的元素值为v的一元二次表达式,将掩模的每个元素都除以16*v*v-48*v+ 32。设m(i, j)为掩模中位值为(i, j)的元素,f (x, y)为掩模作用于图像的中心像素,f (x+i, y+j)为距离中心(i, j)的像素,故可以得到掩模的运算规则为 图2 5*5微分掩模 移动掩模使作用于图像的每一个像素,从而达到图像增强的目的。当像素距离图像边缘小于两个像素时,掩模不能完全覆盖到图像上,此时则不进行运算。 常用而且有效的孤立噪声的消除是中值滤波法,如式(7)所示 其中 med()为集合{X(s, t)}的中值函数,X(s, t)是n*n窗口内的像素。 它把邻域中的图像的像素按灰度级进行排序,然后选择该组的中间值作为输出像素,所以中值滤波对极限像素值不敏感,从而可以消除孤立的噪声点,又可以使图像产生较少的模糊。 形态学是一门建立在严格的数学理论基础上的科学,它利用集合论的方法对物体的几何结构进行分析和处理。在图像分析与处理领域中,将形态学推广至灰度形态学,使用具有一定形态的结构元素来度量和提取图像中的对应的形状,从而达到对图像进行检测和识别等目的。形态学的基本操作有腐蚀、膨胀、开运算、闭运算、击中击不中变换等,具体请参考相关文献[7]。 膨胀运算一般是给图像中的对象边界添加像素,进行膨胀运算时,输出像素值是输入图像相应邻域内所有像素的最大值。用结构元素b对输入图像f进行灰度膨胀如下式所示 其中 DfDb分别是f和b的定义域。 腐蚀运算是删除图像边界元素,输出像素值是输入图像相应像素邻域内所有像素的最小值。用结构元素b对输入图像f进行灰度腐蚀如下式所示 细化就是把输入的具有一定宽度的图像轮廓用逐次去掉边缘的方法最终变为宽度仅为一个像素的骨架,通过细化可以显示图像的拓扑结构,细化通过两步腐蚀如公式来实现。 (1)选择图2所示的5*5分数阶微分掩模算子,为了便于后续检测工作中阈值的设定,将算子的每一项都除以32-48*v+16*v*v,其中v是分数阶微分算子的分数阶数,取 v=0.7(分数阶微分算子具有微分可调的特性,调节分数阶微分的分数阶数可以改变输出像素的变化程度,很容易调节图像的锐化效果,在实验中v=0.7取得了较好的实验效果)。 (2)将第一步运算后所得算子根据式(7)所示的掩模与路面病害图像运算,注意当像素距离图像边缘小于两个像素时,掩模不能完全覆盖到图像上,此时则不进行运算。 (3)把第二步演算后得到的图像的像素值与原图像对应像素相减得到图像的病害边缘信息。 (4)将经过上述增强的图像再实施组合中值滤波,滤除孤立噪声点。 (5)组合使用图像形态学的膨胀腐蚀等算子,提取出路面图像的裂缝。 实验用计算机为 CPU Intel Pentium IV 2.93GHz处理器、1G内存,80G硬盘,编程工具选用Matlab7.0.4。原始图像来自沪宁高速实拍图片,处理图像的尺寸为256*256像素。利用本文算法,对大量图像进行了实验,这里给出有代表性的路面病害图像,图3几种算子对含有较弱信号纵向裂缝的增强结果比较、图4、图5几种算子对纵横交错裂缝的增强结果比较以及用本文算法进行增强,中值滤波和用形态学算子提取裂缝的结果。图6是网状裂缝的增强结果及裂缝的标出结果。 图3、图4、图5和图6中(a)为原输入图像,图3、图4和图5中 (b)、(c)、(d)、(e)是几种经典算法和本文提出算法的比较。其中(b)、(c)为经典1阶Sobel、Prewitt算子演算的结果,(d)为2阶的Laplacian of Gaussian(Log)算子演算的结果,(e)为分数阶数为0.7的分数阶微分算子演算后的结果。从图中可以看出,1阶Sobel和Prewitt梯度算子演算结果比较接近,2阶Log算子演算的结果与本文有些相似。但是,对原图像用几种经典算法演算后得到的结果与本文提出的方法演算后得到的病害图像结果相比,图(e)的病害信息更加清晰,而且保留了更丰富的弱信号信息即对弱信号病害部分的增强比其余算子显著增强。 图3 几种算子对纵向裂缝增强演算结果比较 图4 增强演算结果比较及用本文算法提取裂缝 图5 几种算子演算结果比较及用本文算法提取裂缝 图6 网状裂缝的增强及裂缝的标出结果 图3所示为含纵向弱信号裂缝图像增强。图(e)中弱信号裂缝对比度增强,而且比(b)、(c)、(d)保留了更丰富的弱信号信息。图4所示为复杂裂纹图像增强与检测。图(e)获得的病害信息更加清晰,而且依然保留了更丰富的弱信号信息。图4和图5中(f)、(g)、(h)分别为用本文算法进行二值化,组合中值滤波及用形态学算子实现的裂缝提取结果。图6中(b)为本文算法实现的增强结果,(c)为最终检测到的病害图像,其中病害部分用红色线条标出。 经过大量的实验说明,本算法对于路面图像中弱信号病害的增强效果显著。虽然,本文所采用的算法比传统的方法有很大的改进,病害检测也非常有效,但是,也注意到对于有大量较暗的离散颗粒的图象处理效果还存在缺陷,如图 6(c)中的离散红色点,同时也发现由于摄像机的采光问题导致对于背景光分布特别不均匀的图像会存在误测情况,这也正是后续研究工作的重点之一。 通过分析信号经过微分后的幅频特性,得出基于分数阶微分的图像增强算子比传统的基于1阶和2阶的微分算子具有更高的清晰度,尤其是在平滑区域。根据经典的分数阶微分G-L定义推导出的分数阶微分的差分定义,构建了分数阶微分掩模,通过分数阶微分掩模运算增强路面图像,使处于平滑区域的弱信号裂缝病害信息有效加强。 实验结果表明,本文提出的分数阶微分掩模有很好的图像弱信号增强功能。通过与其它空间滤波算子的效果比较,可以看出,本文设计的分数阶微分算子弥补了传统图像增强算子不能通过改变参数来得到连续变化的增强效果,以及对于较弱信号增强效果不理想的缺陷。同时,自适应阈值的选择也在很大程度上提高了病害检测的效果。由实验结果可以得出结论,基于分数阶微分的病害图像处理方法效果良好,而且,算法更具灵活性和针对性。该方法可以广泛应用于路面图像病害检测。尽管如此,在实验中还是发现对于纹理过于粗糙的图像的处理效果欠佳,存在较多密集的离散点,还存在进一步改进的空间,在后续研究工作中一方面要寻求普遍自适应阈值选取方法;另一方面可以在线条拟合方向展开。 [1]张洪光, 王 祁, 魏 玮. 基于人工种群的路面裂纹检测[J]. 南京理工大学学报, 2005, 29(4):389-393. [2]高建贞, 陆建峰, 赵春霞, 等. 基于多级拟合的道路病害自动检测与识别[J]. 计算机工程与应用, 2004,22: 220-223. [3]唐 磊, 赵春霞, 王鸿南, 等. 基于图像三维地形模型的路面裂缝自动检测[J]. 计算机工程, 2008, 34(5):21-38. [4]王 刚, 贺安之, 肖 亮. 基于高速公路裂纹局部线性特征内容的脊波变换域算法研究[J]. 光学学报,2006, 26(3): 341-346. [5]Pincherle I. Fractional differential equations [M]. San Diego: Academic Press, 1990. 20-23. [6]蒲亦非. 将分数阶微分演算引入数字图像处理[J].四川大学学报(工程科学版). 2007, 39: 124. [7]阮秋琦. 数字图像处理学[M]. 北京: 电子工业出版社, 2001. 430-450.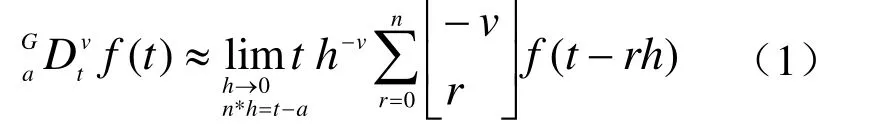
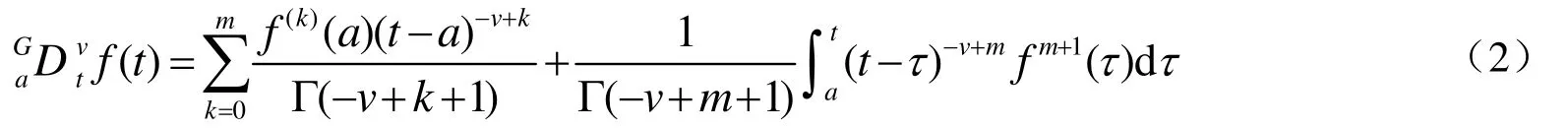
1.2 分数阶微分运算用于图像信号处理
2 构建分数阶微分掩模算子实现路面裂缝检测算法
2.1 构建分数阶微分掩模算子
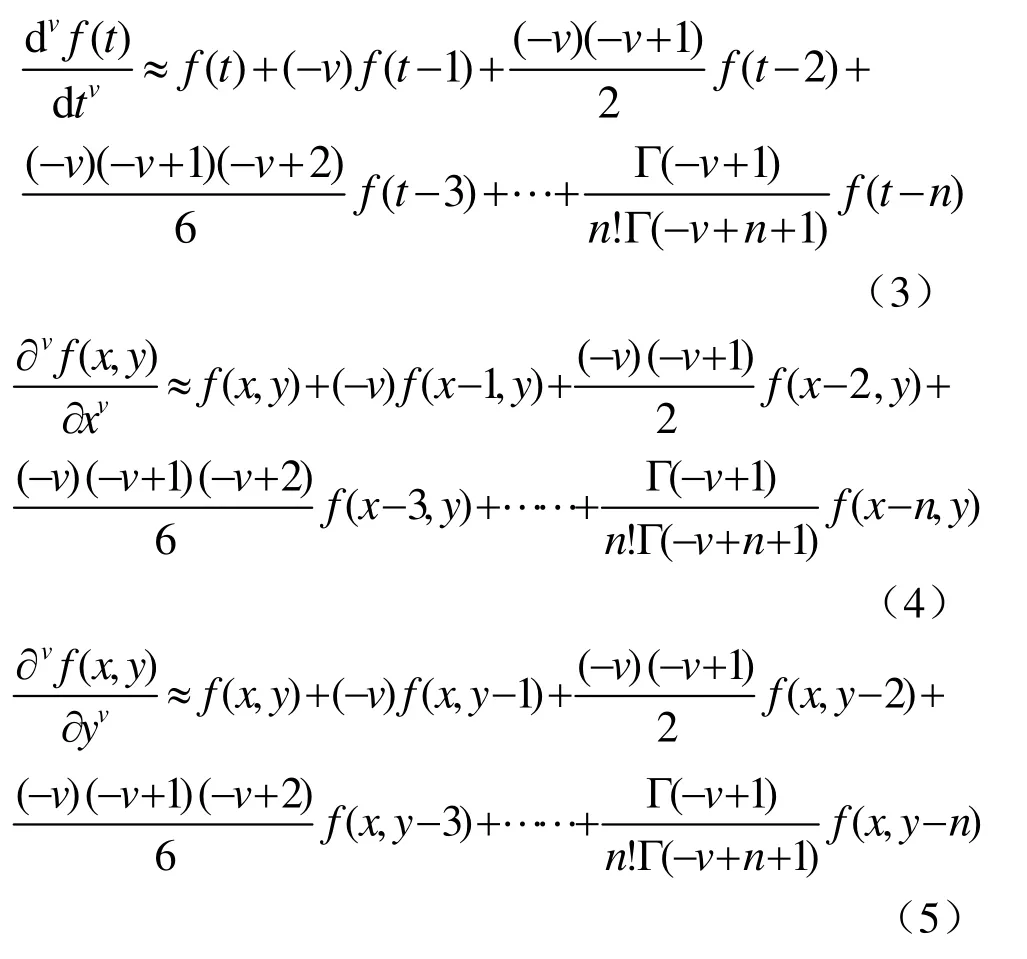
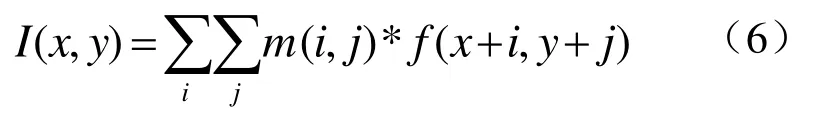

2.2 中值滤波去除孤立噪声
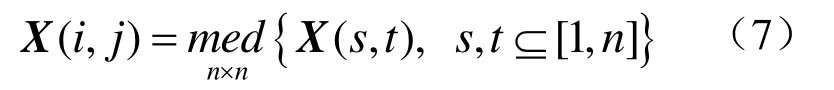
2.3 形态学演算实现路面裂缝提取
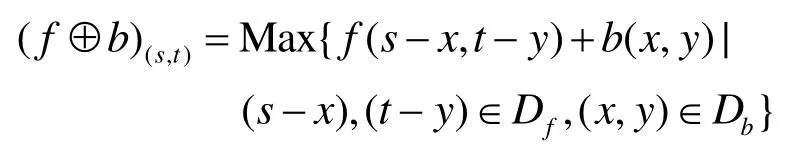
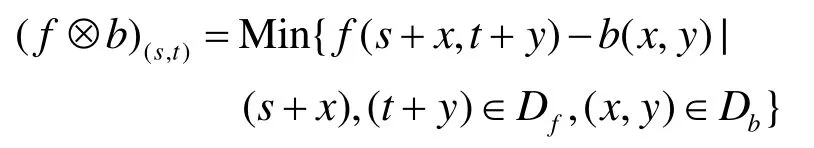
3 实验结果
3.1 实验过程
3.2 结果分析




4 结 论

